Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Ключевое слово: |
|
| Page views: 13877 |
Print version Full issue in PDF (1.30Mb) |
Анализ электрофизиологических сигналов (ЭФС) имеет определенные отличия от анализа сигналов, например, в сейсмической разведке или в гидролокации. При анализе сигналов техногенного характера или отклика физических систем (механических, электромеханических) численные значения параметров сигнала (амплитуда, частота, спектр, автокорреляционная функция) практически всегда связаны с характеристиками исследуемых систем. Например, исследуя время появления эхосигнала и его интенсивность при сейсмическом зондировании земной коры, можно определить характер пластов и глубины их залегания, поскольку в основе метода лежит относительно точная физическая модель процесса. При анализе ЭФС такой модели практически никогда не бывает. Например, достаточно подробно изучена электрическая активность отдельного нейрона (форма импульсов, амплитуда, задержки проведения и т.п.), однако процесс формирования сигнала электроэнцефалограммы (ЭЭГ) разработанной модели не имеет. При анализе ЭЭГ врач-эксперт анализирует кривые, больше опираясь на критерии подобия и ранее встречавшиеся прецеденты, чем на физику процессов, происходящих в мозге. Первоначально применение того или иного метода обработки сигнала подсказывал сам характер соответствующих ЭФС. Часто появление новых методов обработки сигналов объясняется появлением соответствующей новой аппаратуры. Так, всплеск интереса к исследованием поздних потенциалов желудочков (ППЖ) сердца связан с приходом компьютеров в область анализа ЭКГ. Данные ЭФС экспертами-врачами используются не как конкретные числовые величины, а как символьные сообщения на некотором языке описания ЭФС. Весь процесс формирования экспертного заключения по ЭФС подобен трансляции строки на одном (описание ЭФС) в строку на другом (врачебное заключение). Собственно для практического применения используется не результат цифровой обработки ЭФС, а его словесная интерпретация экспертом. Исходя из этого процесс анализа ЭФС следует всегда рассматривать с точки зрения удобства и возможности его дальнейшей интерпретации. В связи с этим особое значение представляет выбор алфавита, то есть основных элементов входного языка описания ЭФС и синтаксиса этого языка. ЭФС, как и любой другой сигнал, может быть представлен в различной форме и различными способами: во временной области, в частной области, автокорреляционной функцией, разложением по определенному функциональному базису. Каждый метод имеет определенные преимущества и может использоваться для описания конкретного ЭФС. Особый интерес представляет описание в виде фраз из двух алфавитов с семантическими связями между фразами. Возможен и другой вариант синхронного описания ЭФС – в виде нескольких фраз из одного алфавита с синхронными семантическими связями между фразами. Обычно это описание многомерных ЭФС (ЭКГ, ЭЭГ). Для анализа ЭФС необходимо произвести сегментацию сигнала на информативные и малоинформативные отрезки, произвести разбиение информативных отрезков на составляющие, перекодировать их в символы некоторого алфавита, и затем методами синтаксического и семантического анализа сформировать словесное заключение. При этом особое значение приобретает первичный анализ ЭФС и его сегментация. Традиционный спектральный анализ, основанный на преобразовании Фурье, эффективен при обработке периодических сигналов. На практике ЭФС не является периодическим, к тому же он известен лишь на ограниченном отрезке времени (или ряде отрезков, разделенных пробелами). Зачастую спектральный состав ЭФС меняется со временем. В этом случае необходим некий “локальный” анализ спектра. С последней задачей хорошо справляется вейвлет-анализ [2,3,7]. Используя разложение по осциллирующим функциям, локализованным как во временной, так и в частотной областях, вейвлет-преобразование отображает исходный одномерный сигнал на плоскость время-частота, характеризуя спектральный состав сигнала в каждый момент времени. В данной работе рассматриваются проблемы, связанные с обработкой сигналов, информация в которых распределена неравномерно по временной оси. При анализе различных подходов к решению данной проблемы предпочтение было отдано вейвлет-анализу. Вейвлеты. Семейство вейвлет-функций генерируется из одной порождающей функции
где a – масштабный множитель, характеризующий растяжение; b – сдвиг вейвлета. В качестве вейвлета
Во-вторых, функция должна быть локализована и во временной, и в частотной областях, то есть области определения функции в физическом пространстве Вейвлет-преобразование w(a,t) сигнала
где
и
и справедливо соотношение, являющееся аналогом теоремы Парсеваля,
обеспечивающее, в частности, равенство энергии в физическом и вейвлет-пространствах. Вейвлет-разложение можно выразить через фурье-образы вейвлета
Это дает возможность связать фурье-спектр сигнала
С помощью (8) получаем соотношение
показывающее, что вейвлет-спектр является сглаженной версией спектра Фурье, а характер сглаживания определяется фурье-образом вейвлета. Выбранная в определении (3) нормировка обеспечивает вейвлет-спектру тот же наклон, что имеет спектр Фурье. Так, если спектр Фурье следует степенной зависимости Приведем в качестве примеров два наиболее часто применяемых вейвлета: действительный вейвлет, называемый "мексиканской шляпой",
и комплексный вейвлет Морле (Morlet):
Для решения задач сегментации используем непрерывное вейвлет-преобразование сигнала ЭКГ, записанного с помощью системы автоматического анализа ЭКГ «Кармин». Частота дискретизации ЭКГ – 400 Гц, разрядность – 12 бит. Для анализа использовался Wavelet toolbox пакета MathLab. Исходный ЭКГ сигнал, изображение вейвлет-коэффициентов на плоскости время-масштаб показаны на рисунке 1. На нижнем графике приводятся линии максимумов коэффициентов преобразования. Видно, что при рассмотрении максимумов коэффициентов на плоскости время-масштаб имеем совокупность линий, аппроксимируемых прямыми. Рассматривая их совместно с временным изображением сигнала, можно заметить, что имеется достаточно большая корреляция этих линий с элементами ЭКГ сигнала. Для другого вейвлет-базиса эти линии могут иметь иной характер. Виды непрерывных вейвлет-функций, пригодных для анализа ЭКГ [6]:
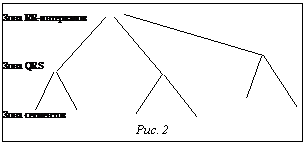
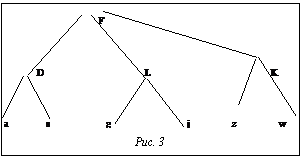
Для перехода от непрерывного вейвлет-анализа к графовому представлению сигнала необходимо рассматривать не всю плоскость время-масштаб, а лишь узлы линий максимумов коэффициентов, при этом различные группы масштабов ответственны за представление различных элементов ЭКГ (рис. 2). Переход от графового представления сигнала к его строковой записи можно осуществить левосторонним обходом дерева узлов вейвлет-коэффициентов, например так, как на рисунке 3. Результирующая строка aDsFgLjzKw – синтаксический образ сигнала – далее обрабатывается синтаксическим анализатором или подвергается сжатию по известным алгоритмам [1]. В результате синтак Практическая реализация данного подхода к анализу сигнала сложной формы выявила сильную чувствительность метода от вида входного сигнала и применяемого вейвлет-базиса. Для исключения пропусков элементов сигнала и ложных обнаружений предлагается последовательно использовать несколько различных базисов, причем один из них должен быть непрерывной функцией (для анализа малоамплитудных низкочастотных компонент), а другой – кусочно-непрерывным вейвлетом для анализа высокоамплитудных, быстро осциллирующих компонент. Данный подход к анализу ЭКГ применяется в системе автоматизированной диагностики ЭКГ «Кармин». Список литературы 1. Синютин С.А. Сжатие электрофизиологических сигналов. //Компьютерные технологии в инженерной и управленческой деятельности. - Таганрог: ТРТУ.- 2000. - С.315-320. 2. Ярцева Е.С. Обработка электрокардиосигнала вейвлет-методом. // Там же. - С.323-326. 3. Захаров В.Г., Фрик П.Г. Применение вейвлет-анализа к задачам исследования загрязнения окружающей среды // Математическое моделирование систем и процессов. - Пермь: ПГТУ. - 1994. - Вып.2. - С. 28-42. 4. Фрик П.Г. Вейвлет-анализ и иерархические модели турбулентности. - Пермь, 1992. (Препр. / ИМСС УрО РАН). 5. Farge M. Wavelet transforms and their applications to turbulence., Ann. Rev. Fluid Mech.,v.24, 1992, 395. 6. Sahambi J.,Tandon S., Bhatt R. Using Wavelet Transforms for ECG characterization, IEEE Engineering in medicine and biology ,v. 16,1997, 77. 7. Frick P., Galyagin D., Hoyt D., Nesme-Ribes E., Schatten K.H., Sokoloff D., Zakharov V. Wavelet analysis of solar activity recorded by sunspot groups.,1996, Astronomy and Astrophysics (in press). 8. Grossmann A., Morlet J. Decomposition of Hardy functions into square integrable wavelets of constant shape, S.I.A.M., J. Math. Anal.,v.15,1984, 723. 9. Holschneider M. Wavelets. An analysis Tool. Oxford: Oxford University Press.1995. |
| Permanent link: http://swsys.ru/index.php?page=article&id=725&lang=en |
Print version Full issue in PDF (1.30Mb) |
| The article was published in issue no. № 1, 2002 |
Perhaps, you might be interested in the following articles of similar topics:
- Сравнение сложных программных систем по критерию функциональной полноты
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Система моделирования и оценки эффективности торговых стратегий
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- О программной реализации геоинформационных систем
Back to the list of articles
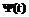 , называемой также анализирующим вейвлетом, при помощи растяжения (сжатия) и сдвига,
, называемой также анализирующим вейвлетом, при помощи растяжения (сжатия) и сдвига,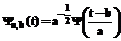 , (1)
, (1)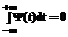 . (2)
. (2)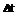 и в пространстве частот
и в пространстве частот 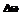 должны удовлетворять условию
должны удовлетворять условию .
. определяется как
определяется как , (3)
, (3)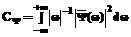 (4)
(4)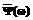 есть фурье-образ вейвлета
есть фурье-образ вейвлета 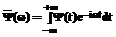 . (5)
. (5)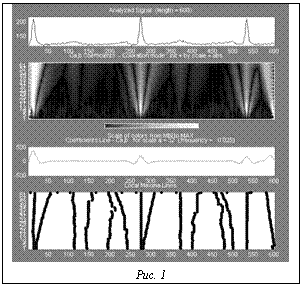 Если
Если 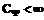 , то для вейвлет-преобразования существует формула обращения
, то для вейвлет-преобразования существует формула обращения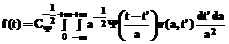 (6)
(6)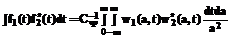 , (7)
, (7)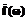 :
: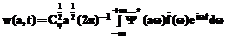 , (8)
, (8)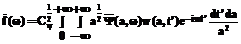 .(9)
.(9)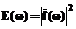 с интегральным вейвлет-спектром, который определяется как энергия, содержащаяся во всех вейвлет-коэффициентах одного масштаба a:
с интегральным вейвлет-спектром, который определяется как энергия, содержащаяся во всех вейвлет-коэффициентах одного масштаба a: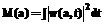 . (10)
. (10) , (11)
, (11)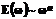 , то интегральный вейвлет-спектр подчиняется тому же степенному закону:
, то интегральный вейвлет-спектр подчиняется тому же степенному закону: 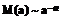 .
.
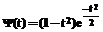 , (12)
, (12)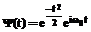 , (13)
, (13)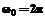 .
.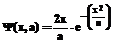 (14)
(14)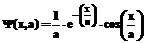 (15)
(15) (16)
(16) сического анализа программно формируется словесное заключение по форме ЭКГ сигнала.
сического анализа программно формируется словесное заключение по форме ЭКГ сигнала.