Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Настройка параметров адаптивного контроллера с использованием нечеткой нейронной сети
Аннотация:
Abstract:
| Автор: Ткач С.Н. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14062 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
Создание прикладных интеллектуальных систем управления и их внедрение в различные сферы человеческой деятельности показали высокую эффективность использования современных информационных технологий при управлении слабо формализуемыми объектами и процессами. Широкое развитие получили так называемые нечеткие системы, использующие средства нечеткого управления. Типичным представителем такой системы является нечеткий контроллер, работающий с базой нечетких правил и реализующий операции нечеткой алгебры при формировании нечеткого вывода. В соответствии с определением 1 из [1] система управления, ориентированная на обработку нечетких знаний, относится к системе управления интеллектуальной в малом. Своим успехом нечеткая логика обязана собственной эффективности и простоте выражения неформальных знаний человека. Однако несмотря на все преимущества нечеткой логики, сегодня не существует формальных процедур проектирования нечетких систем, а доступные методы создания нечетких контроллеров весьма немногочисленны. Основные идеи, использующиеся при построении нечеткой системы управления, основываются на опыте и знаниях разработчика, полученных методом проб и ошибок. Более того, оценить производительность нечеткого контроллера можно только после его создания. Динамическое описание процесса в нечетких системах управления задается базой нечетких правил, с помощью которых имитируется процесс принятия решения человеком при управлении системой. Однако получить приемлемые нечеткие правила, особенно при описании сложного процесса, чрезвычайно трудно. При проектировании нечетких систем управления реального времени на первый план выходят проблемы сложности управляемого процесса и необходимой скорости получения управляющего воздействия. В последнее время появились методы, объединяющие механизмы нечеткого управления и принципы построения нейронных сетей и позволяющие проектировать обучающиеся интеллектуальные системы управления реального времени. Но такие системы имеют один общий недостаток, присущий методам нейронного управления: неясно, как нейронная сеть решает соответствующую задачу управления. В общем случае из сети невозможно извлечь какое-нибудь структурное знание, которое может быть сформулировано, например, в виде правил. Кроме того, нейронная сеть не может использовать какие-либо априорные знания и вынуждена обучаться с самого начала в случае существенных изменений параметров системы. В настоящей статье исследуется новый вид архитектуры нейронной сети, носящий название нечеткой нейронной сети, моделирующей нечеткий логический контроллер. Структура нейронной сети может быть легко проинтерпретирована в терминах нечетких правил нечеткого контроллера. Используемый алгоритм обучения способен настраивать функции принадлежности лингвистических термов входных переменных и выходных параметров системы, а также генерировать новые нечеткие правила для повышения производительности контроллера. В выходном узле нейронной сети применена процедура дефаззификации, основанная на метазнаниях, позволяющая избежать противоречий, возникающих при обычных методах дефаззификации нечетких множеств. На основании вышеизложенного сформулируем нашу задачу: разработка модели нечеткого контроллера на базе нечеткой нейронной сети, способного управлять сложными динамическими системами, с возможностью обучения и добавления новых правил, на основании схе- мы (рис. 1).
Датчики. В каждый момент времени состояние системы характеризуется определенным набором параметров. Значения этих параметров проходят через процедуру фаззификации. Фаззификация – это процесс перевода точных значений параметров, поступающих с датчика, в значения лингвистической переменной. Блок нечетких правил (БНП). В этом блоке производится нечеткий вывод в рамках концепции нечетких правил если-то. Под нечетким правилом если-то понимается правило вида: Если А, то В (А ® В), где А – значения лингвистических переменных, описывающих состояние больного, а В – значения лингвистической переменной, описывающей предпринимаемые действия. Дефаззификация. Функции данного блока являются обратными функциям блока фаззификация. Дефаззификацией будем называть процесс перевода значений лингвистической переменной в точные значения управляющего сигнала. База метазнаний. Существуют примеры [10], в которых использование традиционных методов дефаззификации приводит к неприемлемым результатам. Поэтому необходимы механизмы дефаззификации, основанные на общих знаниях о свойствах выходных параметров системы, которые заложены в блок база метазнаний. Управляющий сигнал. Нечеткий контроллер воздействует на систему посредством управляющих сигналов. В нашем примере управляющим параметром является давление, под которым газовая смесь подается в легкие больного. Процедура обучения необходима для более тонкой настройки функций принадлежности значений лингвистических переменных, а также для генерации новых нечетких правил в случае добавления новых измеряемых и/или регулируемых параметров. Нечеткие правила и нечеткий логический вывод Используя нечеткие множества, динамическое поведение системы можно описать при помощи нечетких правил, основанных на экспертных данных. Обычно эти правила выражаются в форме ЕСЛИ (множество состояний удовлетворяется), ТО (множество следствий можно вывести) следующим образом: ЕСЛИ X есть Аi и Y есть Вi, ТО Z есть Ci. Лингвистические переменные X, Y являются предпосылками правила, а Z – следствием правила. Ai, Bi, Ci суть возможные значения лингвистических переменных. Они называются лингвистическими термами, выражающими понятие нечеткости, и представляются нечеткими множествами. Лингвистические переменные в предпосылках (следствиях) правила образуют нечеткий вход (выход). Терм-множество определяет количество лингвистических термов (нечетких множеств), связанных с каждой лингвистической переменной на входе и выходе системы. Число лингвистических термов предпосылок отражает точность нечеткого представления и определяет максимальное количество правил, которые можно построить. Например, если с лингвистическими переменными Х и Y соотносятся два и три лингвистических термов соответственно, то для описания процесса может быть сформулировано шесть нечетких правил.
Методы дефаззификации Дефаззификация играет важную роль при реализации методов моделирования нечетких систем, использующихся в системах управления. Рассмотрим основные способы дефаззификации. На практике обычно используются метод центра области (ЦО) и метод среднего максимального (СМ). Допустим, что F – нечеткое подмножество множества Х. Нам необходимо найти некоторое дефаззифицированное значение, соответствую- щее F. Первый класс методов дефаззификации – так называемые смешивающие методы (метод ЦО), в которых искомое значение ищется в виде
Существует обобщение этого метода [5,6], заключающееся в том, что нечеткое множество F сначала преобразуется в нечеткое множество Е, после этого находится x*. Преобразование исходного множества может производиться разными способами. Упомянем два важнейших класса преобразований. Преобразования первого класса описываются следующими формулами: mE(x) = 0, mF(x) < K, mЕ(х) = mF(x), mF(x) ³ K. В действительности более интересен для рассмотрения модифицированный метод M* = maxx mF(x), mE(x) = 0, mF(x) < KM*, mE(х) = mF(x), mF(x) ³ KM*. Другой класс преобразований представляется формулой: mE(x) = (mF(x))a. Стоит заметить, если a = 1, тогда мы имеем дело с методом ЦО и если a ® ¥, тогда мы получим метод СМ. Получив множество Е, находим искомое значение
Схема процесса дефаззификации показана на рисунке 2. Следующий класс методов дефаззификации – это методы, выбирающие в качестве решения один из элементов множества Х. Для выбора решения по функции принадлежности mF(x) определяется распределение вероятностей
где рi – вероятность, связанная с решением xi. После определения вероятностей, проводится случайный эксперимент, в котором с вероятностью рi выбирается решение xi. Простейшая процедура, реализующая данный метод, состоит в следующем. 1. Установим а0 = 0, аi = аi – 1 + pi. 2. Пусть si = [аi – 1, аi]. 3. Сгенерируем случайное число g Î [0,1]. 4. Если g Î si, то x* = xi. Аналогично смешивающим методам данный метод можно обобщить, введя преобразование F ® E. Схема процесса дефаззификации показана на рисунке 3. Нечеткая нейронная сеть При оценивании нечетких правил, проблема дефаззификации является одним из узких мест нечеткой системы управления. Часто неочевидно, какое из точных значений наиболее полно характеризует нечеткое множество, полученное системой правил. Наиболее популярным методом дефаззификации является метод центра масс, или метод ЦО, однако, используя этот метод, сложно определить индивидуальный вклад каждого правила в конечный результат. Для преодоления этих трудностей используются монотонные функции принадлежности, предложенные Цукамото, где дефаззификация – это применение обратной функции [11]. В простейшем случае такая функция принадлежности характеризуется двумя точками а, b, определяющими носитель нечеткого множества, в которых m(а) = 0 и m(b) = 1, а в остальных определяется следующим образом:
Таким образом, значение х, соответствующее значению принадлежности y, может быть вычислено при помощи формулы: х = m-1(у) = -y (а - b) + a, где у Î [0,1]. На рисунке 4 показана простая нечеткая нейронная сеть, включающая два нечетких правила R1: ЕСЛИ Т – НИЗКАЯ И Н – НЕВЫСОКАЯ ТО Х – НИЗКАЯ, R2: ЕСЛИ Т – ВЫСОКАЯ И Н – НЕВЫСОКАЯ ТО Х – ВЫСОКАЯ, где НИЗКАЯ, ВЫСОКАЯ и НЕВЫСОКАЯ – термы соответствующих лингвистических переменных, окружности представляют узлы сети, а прямоугольники – нечеткие веса.
Узлы правил Rj принимают все приходящие значения принадлежности и, используя T-norm оператор, например оператор min, вычисляют конъюнкцию предпосылок. Эти действия производятся всеми узлами параллельно. Затем состояния узлов посылаются на выходной слой, состоящий из одного или более узлов, описывающих управляющее воздействие. Веса соединений между промежуточным и выходным слоями – это функции принадлежности nk термов вывода правила. Вычисления, выполняемые на соединениях, представляют нечеткую импликацию. В результате получается нечеткое множество Каждый выходной узел принимает нечеткие множества, агрегирует их и при помощи подходящей процедуры дефаззификации D определяет точное выходное значение.
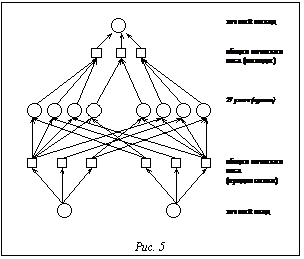
где m – число правил, а rj – результат вывода правила Rj. Следовательно, для построения нечеткой нейронной сети необходимо определить входные и выходные переменные, для каждой переменной выбрать начальные неоптимальные терм-множества, описываемые лингвистическими термами, например, НИЗКАЯ, ВЫСОКАЯ и т.п. Если нечеткие правила неизвестны, то мы должны создать сеть, представляющую все правила, которые можно сформулировать при помощи всех термов всех переменных. Например, если мы имеем MISO (multiple input single output) систему с двумя входными переменными и пятью термами для каждой из них, то мы должны построить нечеткую нейронную сеть с 2 входными узлами, 1 выходным узлом и 53 = 125 промежуточными узлами. На рисунке 5 приведен пример нечеткой сети с тремя термами для каждой переменной. Дефаззификация с использованием метазнаний
Суть метода заключается в следующем. Во-первых, достаточно очевидно, что процесс дефаззификации будет более эффективен, если мы воспользуемся некими метазнаниями, определяющими возможность объединения двух возможных решений. Во-вторых, процесс дефаззификации может рассматриваться как более общая задача кластеризации (clustering problem). Действительно, в стандартном методе дефаззификации, методе ЦО, мы предполагаем, что множество решений – это группа (cluster), а само решение – это центр группы (cluster’s center). Эти соображения позволяют нам позаимствовать некоторые идеи из теории нечеткого группирования (fuzzy clustering theory) [10]. Предположим, что мы имеем некую базу правил, определяющих возможность сочетания двух вероятных решений. В частности, допустим, что задано соотношение R: X´X ® [0, 1], определяющее для каждой пары x, y Î X возможность объединения решений х и у. Допустим также, что соотношение R симметрично, то есть R(x,y) = = R(y,x), и что большее значение R(x,y) соответ- ствует большей возможности сочетания реше- ний х и у. Следовательно, R(x,y) = 0 соответствует двум несочетаемым решениям. Также предположим, что R(x,x) = 1. Пусть F – нечеткое подмножество множества X, которое необходимо дефаззифицировать. Обозначим множество F как F1 и найдем х1 такой, что
Затем вычислим F2:
Иными словами, мы предполагаем, что х1 – это центр кластера, и пытаемся найти другой центр, в котором влияние х1 наименьшее. Фактически, х1 – это пробное решение. Очередной шаг – нахождение следующего пробного решения
Теперь построим F3:
Следуя далее согласно этой процедуре, получим
где xi такое, что
Процесс заканчивается, когда максимальное значение Далее находим модифицированные пробные решения, связанные с кластером каждого пробного центра xi
После этого вычисляем оценку Тi, связанную с i-м кластером
Итак, мы имеем пробные решения и связанные с ними оценки Тi. Теперь необходимо выбрать один из этих элементов в качестве решения. Определим распределение вероятностей
При помощи случайного эксперимента получаем дефаззифицированное решение. Следуя приведенным рассуждениям, модифицируем процедуру дефаззификации в нечеткой нейронной сети. Пусть C нечеткое множество, состоящее из элементов {
Вычислим С2
Продолжаем определение Сi, пока
Определяем оценки Тi и вычисляем распределение вероятностей
Проведя случайный эксперимент, мы получим в качестве решения один из элементов rj = rj×R( Таким образом, процедура дефаззификации дает решение, существенно опираясь на метазнания, выраженные в виде функции сочетания R(x,y). Обратное распространение нечеткой ошибки и обучение правилам Наша цель – настройка функций принадлежности нечеткой нейронной сети при помощи обучающей процедуры. В силу того, что обычно невозможно определить оптимальное управляющее воздействие во время работы контроллера и, следовательно, нельзя подсчитать ошибку непосредственным сравнением, мы должны получить меру, адекватно описывающую состояние системы. Оптимальное состояние системы может быть описано как вектор в пространстве состояний системы. Это означает, что если система достигла желаемого состояния, то все переменные состояния достигли значений, определенных этим вектором. Поэтому естественно определить степень приближения текущего состояния к оптимальному при помощи функции принадлежности, из которой мы сможем вывести нечеткую ошибку, характеризующую производительность нечеткой нейронной сети. Рассмотрим систему с n переменными состояния Х1, …, Хn. Определим нечеткую степень приближения состояния к оптимальному G1 как
где функции принадлежности В дополнение мы будем трактовать состояния как хорошие, если неправильные значения одних переменных компенсируются значениями других таким образом, что система движется к желаемому состоянию. Определим нечеткую степень G2 как G2 =
где функции принадлежности Общая нечеткая степень приближения вычисляется как G = g(G1, G2), где операция g определяется исходя из поставленной задачи. В одних случаях это может быть операция min, в других – более сложная операция, зависящая, допустим, от знака текущих переменных состояния. Например, мы будем использовать G1, если все переменные или положительные, или отрицательные, и G2, если они как положительные, так и отрицательные. Нечеткую ошибку нечеткой нейронной сети (она нужна для настройки функций принадлежности) определим следующим образом E = 1 – G. В дополнение к этой оценке ошибки нам необходима дополнительная мера, с помощью которой мы будем определять, какие узлы правил следует удалять из сети. Для этого следует определить желательность перехода между двумя состояниями. Этим самым мы сможем вывести нечеткую ошибку перехода Et Et = 1 – min{ti(Dxi)| i Î {1,…,n}}, где Dxi – изменение переменной Xi, а ti – функция принадлежности, дающая нечеткое представление желаемого изменения соответствующей переменной. Теперь мы можем построить алгоритм обучения. Для каждого узла правила Rj известно значение конъюнкции его предпосылок rj и значение следствия Процедура обучения состоит из трех шагов. На шаге 1 все правила, приводящие к редуктивному результату, например к отрицательным значениям там, где требуются положительные и наоборот, удаляются. Более того, каждое правило имеет счетчик, уменьшающийся всякий раз, когда правило не используется, то есть rj = 0. В противном случае, когда rj ¹ 0, счетчик устанавливается в максимальное значение. На шаге 2 уже не существует узлов правил, имеющих одинаковые предпосылки и приводящих к противоположным следствиям. Для получения корректной базы правил необходимо из группы правил с одинаковыми предпосылками выбрать только одно правило. Для этого на шаге 2 оцениваются все счетчики, связанные с узлами правил. Как только счетчик достигнет 0, соответствующий узел правила удаляется. Далее каждому правилу ставится в соответствие собственное значение ошибки, которое накапливает нечеткую ошибку перехода: если правило вносит редуктивный результат, Et добавляется без изменений, если нет, то Et взвешивается нормированной разностью между выходным значением правила и выходным значением всей сети. В конце шага 2 из каждой группы узлов правил с одинаковыми предпосылками, оставляется узел с наименьшим значением ошибки, все остальные узлы удаляются. Таким образом, получается сеть с минимальным количеством узлов, необходимых для управления процессом. На шаге 3 производительность нечеткой нейронной сети улучшается путем настройки функций принадлежности. Считаем, что мы используем монотонные функции принадлежности Цукамото. Каждая функция принадлежности характеризуется парой (a, b), такой что m(a) = 0, а m(b) = 1. Для того чтобы сделать правило более чувствительным, необходимо увеличить расстояние между этими двумя значениями в каждой из предпосылок правила. Это достигается изменением значения a, в свою очередь значение b остается неизменным. То есть функция принадлежности сохраняет значения, определяемые b, и изменяет a, увеличивая диапазон |b – a|. Чтобы сделать правило менее чувствительным, этот диапазон следует уменьшить. В дополнение к изменениям в предпосылках необходимо также изменить функцию принадлежности следствия правила. Если правило приводит к хорошему управляющему воздействию, это значение может быть улучшено путем уменьшения разности |b – a|, при плохом управляющем воздействии разность |b – a| следует увеличить. Выходному узлу C необходимо знать направление значения оптимального управляющего воздействия copt. Конечно, само значение неизвестно, но по наблюдениям за текущим состоянием системы может быть определено его направление, например, необходимо приложить положительную или отрицательную силу, то есть известен sign(copt). В выходном узле для каждого узла правила Rj вычисляется собственная ошибка пра- вила
Изменения в функциях принадлежности nk соединений между промежуточным слоем и выходным слоем определяются следующим образом
где s – коэффициент обучения, nk – соединение Rj c C. Если вес nk используется несколькими узлами, то он изменяется выходным узлом столько раз, сколько узлов правил используют этот вес. После этого ошибки правил распространяются обратно на промежуточный слой, где узлы правил изменяют функции принадлежности своих предпосылок:
где входной узел Xi соединен с Rj через После процедуры обучения мы можем проинтерпретировать структуру сети. Оставшиеся узлы правил обозначают нечеткие правила если-то, необходимые для управления динамической системой. Нечеткие веса представляют функции принадлежности лингвистических термов, являющихся значениями входных и выходных переменных. В заключение отметим, что в данной статье рассмотрена модель нечеткого контроллера с использованием нечетких нейронных сетей, способных выполнять обучение и настройку параметров контроллера, и предложена структура нечеткой нейронной сети, которую можно легко интерпретировать в терминах нечетких правил если-то. Рассмотрена процедура обучения, способная как настраивать функции принадлежности термов лингвистических переменных, используемых контроллером, так и получать новые нечеткие правила. Стоит отметить возможность добавления априорных знаний без дополнительного обучения сети. Преложенная процедура дефаззификации, использующая метазнания, выраженные в виде функции сочетания, позволяет избежать затруднения, присущие традиционным методам, при получении точного решения. Одним из главных достоинств предложенной модели является ее принципиальная открытость, позволяющая легко модернизировать контроллер. Список литературы 1. Захаров В.Н., Ульянов С.В. Нечеткие модели интеллектуальных промышленных регуляторов и систем управления. //Изв. РАН. Техн. кибернетика. - 1992. - №5; 1993. - №4. 2. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. - М.:Мир, 1976. 3. Аверкин А.Н., Батыршин И.З., Блишун А.Ф. Нечеткие множества в моделях управления и искусственного интеллекта. - М.:Наука, 1986. 4. Yager R.R. Knowledge-based defuzzification. Fuzzy Sets and Systems 80, 1996. p.177-185. 5. Saaty T.L. Measuring the fuzziness of sets. Journal of Cybernetics, 1974. V.4 p.53-61. 6. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. - М.: Наука, 1990. 7. Filev D.P., Yager R.R. A generalized defuzzification method under BAD distributions. Internat. J. Intelligent Systems 6, 1991. p.687-697. 8. Yager R.R. Filev D.P. On the issue of defuzzification and selection based on a fuzzy set. Fuzzy Sets and Systems 55, 1 993. p.255-272. 9. Hamid R. Berenji A reinforcement learning-based architecture for fuzzy logic control. Int. J. Approx. Reas. 6/2, 1992. p.267-292. 10. Bezdek J.C. Pattern recognition with fuzzy objective function algorithms. N.Y. Platinum Press, 1981. 11. Nauck D., Kruse R. A neural fuzzy controller learning by fuzzy error propagation. Proc. NAFIPS’92, 1992. p.388-397. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=837 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
| Статья опубликована в выпуске журнала № 3 за 2001 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Компьютер - хранитель домашнего очага
- Вычислительный интеллект: немонотонные логики и графическое представление знаний
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Формирование программ развития больших систем административно-организационного управления
Назад, к списку статей



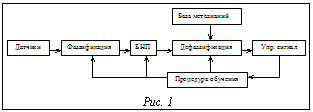 Дадим краткую характеристику каждому из блоков схемы.
Дадим краткую характеристику каждому из блоков схемы.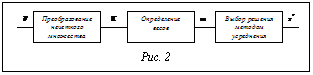 Рассмотрим динамическую систему S, управляемую одним параметром С и описываемую n переменными X1,…, Xn. Каждая переменная имеет область значений Н = [h1, h2], заданы отображения m: [h1, h2] ® [0,1], имеющие смысл функций принадлежности значений лингвистических переменных. Управляющее воздействие, приводящее систему S в желаемое состояние, будем описывать нечеткими правилами вида если-то. Согласно концепции нечеткого логического вывода конъюнкция значений входных переменных определяет значение, соответствующее выходному параметру. Все правила обрабатываются параллельно, их выход образует нечеткое множество, которое для получения точного значения необходимо дефаззифицировать. В качестве T-norm оператора, использующегося в конъюнкции входных значений, обычно применяется оператор min, а в качестве S-norm оператора для агрегирования выходных значений нечетких правил – оператор max (процедура Заде-Мамдани).
Рассмотрим динамическую систему S, управляемую одним параметром С и описываемую n переменными X1,…, Xn. Каждая переменная имеет область значений Н = [h1, h2], заданы отображения m: [h1, h2] ® [0,1], имеющие смысл функций принадлежности значений лингвистических переменных. Управляющее воздействие, приводящее систему S в желаемое состояние, будем описывать нечеткими правилами вида если-то. Согласно концепции нечеткого логического вывода конъюнкция значений входных переменных определяет значение, соответствующее выходному параметру. Все правила обрабатываются параллельно, их выход образует нечеткое множество, которое для получения точного значения необходимо дефаззифицировать. В качестве T-norm оператора, использующегося в конъюнкции входных значений, обычно применяется оператор min, а в качестве S-norm оператора для агрегирования выходных значений нечетких правил – оператор max (процедура Заде-Мамдани).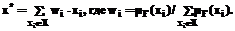
 Заметим, что данная формула существенно объединяет все предложенные решения, и в некоторых случаях приводит к возникновению проблем.
Заметим, что данная формула существенно объединяет все предложенные решения, и в некоторых случаях приводит к возникновению проблем.
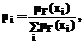
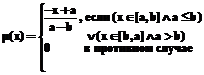 .
.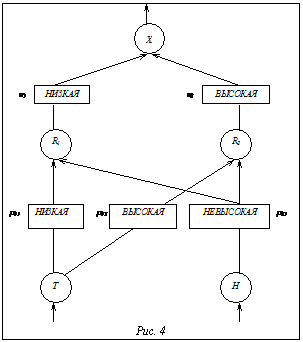 Сеть состоит из трех слоев. Первый, входной слой, содержит узлы, соответствующие входным переменным (по одному узлу на каждую переменную). Состояния этих узлов отражают точные значения параметров. Промежуточный слой – слой правил. Он содержит узлы, соответствующие нечетким правилам (по одному узлу на каждое правило). Состояние каждого узла правила представляет значение принадлежности, найденное при помощи конъюнкции предпосылок правила. Точные входные значения посылаются узлам правил по соответствующим соединениям. Каждое соединение имеет нечеткий вес, образующий комбинацию с входным значением. В нашем случае веса – это функции принадлежности mik термов входных переменных. Комбинация веса mik и точного входного значения xi – это значение принадлежности mik(xi). Если входная переменная с одним и тем же лингвистическим значением используется в более чем одном правиле, то она связывается с соответствующими узлами правил соединениями с одним и тем же весом (см. табл. и рис. 4, вес m21). Использование одного и того же веса – важный аспект предлагаемой архитектуры. Мы пытаемся интерпретировать поведение сети и, следовательно, нам необходимы одинаковые функции принадлежности для одинаковых термов лингвистической переменной.
Сеть состоит из трех слоев. Первый, входной слой, содержит узлы, соответствующие входным переменным (по одному узлу на каждую переменную). Состояния этих узлов отражают точные значения параметров. Промежуточный слой – слой правил. Он содержит узлы, соответствующие нечетким правилам (по одному узлу на каждое правило). Состояние каждого узла правила представляет значение принадлежности, найденное при помощи конъюнкции предпосылок правила. Точные входные значения посылаются узлам правил по соответствующим соединениям. Каждое соединение имеет нечеткий вес, образующий комбинацию с входным значением. В нашем случае веса – это функции принадлежности mik термов входных переменных. Комбинация веса mik и точного входного значения xi – это значение принадлежности mik(xi). Если входная переменная с одним и тем же лингвистическим значением используется в более чем одном правиле, то она связывается с соответствующими узлами правил соединениями с одним и тем же весом (см. табл. и рис. 4, вес m21). Использование одного и того же веса – важный аспект предлагаемой архитектуры. Мы пытаемся интерпретировать поведение сети и, следовательно, нам необходимы одинаковые функции принадлежности для одинаковых термов лингвистической переменной. , описывающее вывод каждого правила Rj. Узлы правил с одинаковыми выходными лингвистическими значениями соединяются с соответствующим выходным узлом через один и тот же вес. В этом случае в выходной узел приходит более одного значения (см. табл. 1).
, описывающее вывод каждого правила Rj. Узлы правил с одинаковыми выходными лингвистическими значениями соединяются с соответствующим выходным узлом через один и тот же вес. В этом случае в выходной узел приходит более одного значения (см. табл. 1).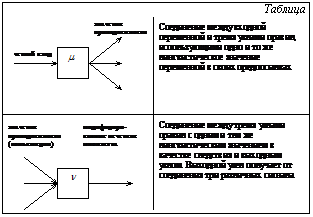 Для обучения нечеткой нейронной сети необходимо знать, какую долю в конечный результат вносит каждое правило, следовательно, в следствиях нечетких правил необходимо использование монотонных функций принадлежности. Таким образом, мы приходим к использованию метода Цукамото для нечеткого вывода, в котором агрегирование и дефаззификация выполняются на одном шаге. Четкое значение с (активирование выходного узла) вычисляется по формуле
Для обучения нечеткой нейронной сети необходимо знать, какую долю в конечный результат вносит каждое правило, следовательно, в следствиях нечетких правил необходимо использование монотонных функций принадлежности. Таким образом, мы приходим к использованию метода Цукамото для нечеткого вывода, в котором агрегирование и дефаззификация выполняются на одном шаге. Четкое значение с (активирование выходного узла) вычисляется по формуле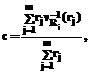
 Как было отмечено, при построении нечетких логических систем для дефаззификации обычно используются метод ЦО и метод СМ, например, в случае нечеткой нейронной сети, применяется метод ЦО. Эти две процедуры могут рассматриваться как взвешенное агрегирование, объединяющее возможные решения. Хотя в большинстве случаев стандартные методы дефаззификации дают неплохие результаты, существуют примеры [10], в которых использование таких процедур приводит к неудовлетворительным решениям. Основная проблема, возникающая при использовании данных методов, состоит в существовании двух или более различных решений, объединение которых приводит к неприемлемому результату. В такой ситуации необходимо определить, в каких случаях мы можем объединять решения, а в каких нет. Далее мы рассмотрим общий подход к проблеме дефаззификации, который поможет нам избежать затруднения, присущие традиционным методам дефаззификации.
Как было отмечено, при построении нечетких логических систем для дефаззификации обычно используются метод ЦО и метод СМ, например, в случае нечеткой нейронной сети, применяется метод ЦО. Эти две процедуры могут рассматриваться как взвешенное агрегирование, объединяющее возможные решения. Хотя в большинстве случаев стандартные методы дефаззификации дают неплохие результаты, существуют примеры [10], в которых использование таких процедур приводит к неудовлетворительным решениям. Основная проблема, возникающая при использовании данных методов, состоит в существовании двух или более различных решений, объединение которых приводит к неприемлемому результату. В такой ситуации необходимо определить, в каких случаях мы можем объединять решения, а в каких нет. Далее мы рассмотрим общий подход к проблеме дефаззификации, который поможет нам избежать затруднения, присущие традиционным методам дефаззификации.
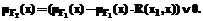
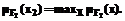
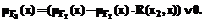
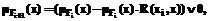

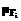 будет меньше некоторого d. В результате мы получим q различных пробных решений х1, х2, ..., хq.
будет меньше некоторого d. В результате мы получим q различных пробных решений х1, х2, ..., хq.

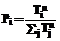 .
. , rj | j = 1,...m}, где m - число правил,
, rj | j = 1,...m}, где m - число правил,  - точное значение, а rj - значение принадлежности, полученное j-м правилом. Обозначим С как С1 и найдем с1 такой, что
- точное значение, а rj - значение принадлежности, полученное j-м правилом. Обозначим С как С1 и найдем с1 такой, что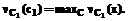
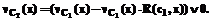
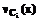 больше некоторого d. После завершения процедуры имеем k пробных решений. Для каждого пробного решения вычисляем дефаззифицированное значение
больше некоторого d. После завершения процедуры имеем k пробных решений. Для каждого пробного решения вычисляем дефаззифицированное значение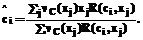
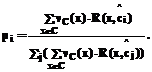
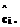 Оценки принадлежности rj модифицируются согласно формуле
Оценки принадлежности rj модифицируются согласно формуле ).
).
 определяются исходя из конкретных требований системы.
определяются исходя из конкретных требований системы.
 также определяются согласно требованиям системы. Более того, может существовать более одной
также определяются согласно требованиям системы. Более того, может существовать более одной  . В силу того, что мы используем монотонные функции принадлежности,
. В силу того, что мы используем монотонные функции принадлежности, 
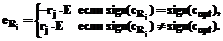
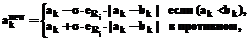

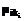 , ki Î {1, …, si}, si – число значений Xi. Если вес
, ki Î {1, …, si}, si – число значений Xi. Если вес 