Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программа моделирования процесса непрерывного литья цветных металлов и их сплавов
Аннотация:
Abstract:
| Авторы: Жиганов Н.К. (iganov2005@yandex.ru) - Тверской государственный технический университет, г. Тверь, Россия, доктор физико-математических наук, Фомина Е.Е. (f-elena2008@yandex.ru) - Тверской государственный технический университет (доцент), г. Тверь, Россия, кандидат технических наук | |
| Ключевые слова: моделирование, цветные металлы, литье |
|
| Keywords: modeling, non-ferrous metals, |
|
| Количество просмотров: 19049 |
Версия для печати Выпуск в формате PDF (1.92Мб) |
Традиционные технологии получения литых заготовок из цветных металлов и их сплавов методом непрерывного литья уже не могут обеспечить соответствующие современным требованиям характеристики заготовок, которые в основном и определяют характеристики готовых изделий. Отсюда практическая потребность в детальном изучении процессов, происходящих при непрерывном и полунепрерывном литье цветных металлов и их сплавов. К наиболее важным явлениям, сопровождающим процесс непрерывного литья, относятся: - движение пограничного слоя затвердевания; - непрерывно меняющиеся температурные условия в течение процесса фазовых переходов; - повышенная индуцированная и поверхностная конвекция; - турбулентность течения; - комбинированный теплоперенос: проводимость-излучение; - нестационарность процесса.
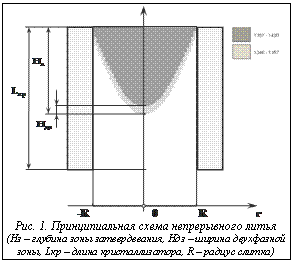
С этой целью была разработана математическая модель и на ее основе написана программа для моделирования стационарных и нестационарных процессов непрерывного литья цилиндрических заготовок (Свид. об офиц. регистр. программы для ЭВМ №2007614353 от 12.10.2007 г.), учитывающая тепловые и гидродинамические процессы [1], принципиальная схема которых приведена на рисунке 1. Затвердевшая заготовка радиуса R вытягивается из кристаллизатора длинною L с постоянной скоростью. Расплавленный металл поступает в кристаллизатор равномерно по всей площади входного отверстия кристаллизатора. Процесс непрерывного литья рассматривается на тепловом и гидродинамическом уровне. При определении условий теплопередачи на границе отливка-кристаллизатор учитывалось образование зазора вследствие развития объемной усадки сплава. Это приводит к резкому снижению интенсивности охлаждения отливки за счет изменения механизма теплопереноса от теплопроводности на излучение и конвекцию. Учет гидродинамических процессов существенно расширяет область применения разработанной программы, так как позволяет явно учитывать влияние конвективного перемешивания расплава в зоне кристаллизации, различных способов подвода расплавленного металла в кристаллизатор, а также явления турбулентности на формирование слитка. В программе предусмотрена возможность моделирования процесса литья с вытяжкой заготовки вверх и вниз. В основу программы положена математическая модель, включающая в себя уравнения неразрывности, теплопроводности, движения Навье–Стокса, турбулентного течения, а также граничные условия в форме уравнений, описывающих тепловой поток на границе. Модифицированная система дифференциальных уравнений [2] решалась методом контрольных объемов [3]. Расчетная область разбивалась на конечное число непересекающихся контрольных объемов так, что в каждом объеме содержался только один узел сетки. Дискретные аналоги получались путем интегрирования соответствующих уравнений по каждому контрольному объему. Интегралы вычислялись с использованием кусочных профилей, описывающих изменение функций между узловыми точками. Все дискретные аналоги были построены с использованием шахматной сетки, компоненты скорости на которой рассчитываются на гранях контрольных объемов, а значения давления и температуры – в узловых точках. Для коррекции полей давления и скоростей применялся метод нижней релаксации [4]. Для моделирования турбулентности использовалась стандарная
Для обеспечения работоспособности программ необходимы следующие технические характеристики: · тип процессора: Pentium 2 и выше; · графический интерфейс пользователя; · расчетная сетка: прямоугольная с автоматической генерацией; · возможности моделирования: двухмерные стационарные и нестационарные, турбулентные и ламинарные течения. Программа включает следующие программные модули: - модуль генерации сетки по рассматриваемой геометрии (вертикальная цилиндрическая труба); - модуль подготовки и ввода исходных данных: длина кристаллизатора, длина и радиус заготовки, диаметр входных отверстий для литья, диаметр отверстий для дополнительного подогрева, скорость литья; а также характеристики металла: плотность, теплопроводность, вязкость, теплоемкость и др.; - модуль для расчета теплового процесса при литье через кольцевые пристеночные отверстия; - расчетный модуль теплового процесса; - расчетный модуль полей скоростей; - опция для расчета нестационарных течений; - модуль для расчета давления, вязкости, кинетической энергии и скорости диссипации; - модули вывода и анализа результатов, представляемых следующим образом: · для температуры – в виде таблицы значений в каждой узловой точке сетки и в виде графика распределения температур в продольном сечении формы; · для давления, вязкости, кинетической энергии и скорости диссипации кинетической энергии – в виде таблицы значений величин в каждой точке сетки; · для скорости – в виде таблиц со значениями радиальной и продольной составляющих скорости, а также в виде графика с векторами скорости по всему продольному сечению слитка. Как показывает технологическая практика, при непрерывной вытяжке заготовки происходит нарушение устойчивости процесса, что может привести к обрыву заготовки. В связи с этим используют полунепрерывную вытяжку с периодическими остановами для улучшения охлаждения заготовки. Это снижает вероятность обрывов, однако приводит к снижению производительности технологического оборудования, потому весьма важным является определение минимально допустимой продолжительности этих остановов. Для решения задачи был выполнен ряд вычислительных экспериментов для нестационарного непрерывного процесса литья медного слитка с вытяжкой вниз и вверх. Значения основных параметров литья: длина кристаллизатора Lкр=0,8 м, размеры слитка L=1 м и r=0,1 м, температура охлаждающей воды в кристаллизаторе 295 К, температура ликвидуса и солидуса 1357 K и 1346 K соответственно, температура заливки расплава в кристаллизатор 1430 K. В качестве примеров моделирования на рисунках 2 и 3 показаны временные срезы температурных профилей по высоте кристаллизатора, рассчитанные для вытяжки вниз и вверх со скоростью 0,06 м/с и 0,04 м/с соответственно, с дискретностью процесса 2 с (вытяжка и останов чередуются с интервалом 2 с). Наибольший практический и теоретический интерес представляет расположение, форма и размеры двухфазной зоны затвердевающего слитка, поскольку именно в ней формируется кристаллическая структура металла и закладываются будущие свойства заготовки. Как показывает опыт и проведенные расчеты, величина этой зоны, а также ее расположение внутри слитка зависят от типа металла, размера заготовки и технологических параметров литья. Разработанная программа позволяет установить количественные отношения между этим параметрами и, следовательно, управлять процессом формирования заготовки. Она может быть использована в производственной практике для решения задач проектирования и оптимизации технологических процессов получения непрерывнолитых заготовок. Список литературы 1. Жиганов Н.К., Вольнов И.Н., Фомина Е.Е. Моделирование процессов непрерывного литья цветных металлов и их сплавов. - Тверь: ТГТУ, 2007. - 224 с. 2. Shyy W., Wei D.Y., Pang Y.//IHMT. 1992. Vol. 35.№ 5. P. 1229-1245. 3. Патанкар C. Численные методы решения задач теплообмена и динамики жидкости. - М.: Энергоатомиздат, 1984. - 152 с. 4. Флетчер К. Вычислительные методы в динамике жидкостей: В 2 т. - М.: Мир, 1991. 5. www.flow3d.com/apps/cast/app_cast_contin_1.html 6. www.flow3d.ru/appl/tundish.htm |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=84 |
Версия для печати Выпуск в формате PDF (1.92Мб) |
| Статья опубликована в выпуске журнала № 1 за 2008 год. | |
| Статья находится в категориях: Научные исследования | |
| Статья относится к отраслям: Металлургия | |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Моделирование оптимальных условий биосинтеза
- Разработка и исследование гибридного метода генетического программирования
- Моделирование информационных процессов систем управления большими данными для решения задач кибербезопасности
- Программная система исследований динамики технологических процессов формования химических волокон
- Программная среда расчетных сеточных моделей для параллельных вычислений
Назад, к списку статей



 Одновременный учет всех этих факторов при моделировании является весьма сложной задачей. Проблема усугубляется также и необходимостью учета конструктивных характеристик конкретных установок литья, влияющих на свойства получаемых заготовок. Экспериментальное изучение этих процессов является трудоемким, дорогостоящим, а зачастую и невозможным процессом. Поэтому актуальным является математическое моделирование и разработка специальных литейных пакетов, позволяющих с приемлемой точностью отразить данные физические процессы и с достаточной наглядностью визуализировать непрерывное литье.
Одновременный учет всех этих факторов при моделировании является весьма сложной задачей. Проблема усугубляется также и необходимостью учета конструктивных характеристик конкретных установок литья, влияющих на свойства получаемых заготовок. Экспериментальное изучение этих процессов является трудоемким, дорогостоящим, а зачастую и невозможным процессом. Поэтому актуальным является математическое моделирование и разработка специальных литейных пакетов, позволяющих с приемлемой точностью отразить данные физические процессы и с достаточной наглядностью визуализировать непрерывное литье.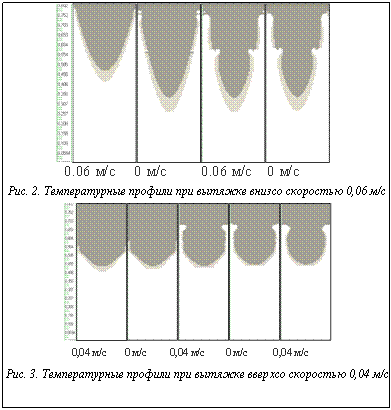 Сравнение разработанного пакета с коммерческим СFD-пакетом FLOW-3D® (www.flow3d.com, www.flow3d.ru), программный код которого многократно тестировался на адекватность экспериментальным данным различных технологических процессов литья, включая непрерывное литье [5,6], показало сопоставимость результатов (расхождение не более 1,2 %). В сравнении с коммерческим пакетом общего назначения FLOW-3D® разработанная программа имеет специализированную, узкую область применения и вследствие этого время расчета на этой программе значительно (на несколько порядков) ниже, чем на FLOW-3D®, она также проста в использовании.
Сравнение разработанного пакета с коммерческим СFD-пакетом FLOW-3D® (www.flow3d.com, www.flow3d.ru), программный код которого многократно тестировался на адекватность экспериментальным данным различных технологических процессов литья, включая непрерывное литье [5,6], показало сопоставимость результатов (расхождение не более 1,2 %). В сравнении с коммерческим пакетом общего назначения FLOW-3D® разработанная программа имеет специализированную, узкую область применения и вследствие этого время расчета на этой программе значительно (на несколько порядков) ниже, чем на FLOW-3D®, она также проста в использовании.