Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Кубический алгоритм генерации трехмерной треугольной сетки
Аннотация:
Abstract:
| Авторы: Чучалин А.И. () - , Королев С.Ф. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14108 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
Многие инженерные задачи и научные исследования требуют решения сложных дифференциальных уравнений с частными производными для трехмерных объектов. В таких случаях обычно используются численные методы математического моделирования, требующие дискретизации исследуемых объектов. Если объектов несколько и форма их сложная, чаще всего применяется метод конечных элементов (МКЭ). В данном методе трехмерные объекты делятся на малые выпуклые многоугольники с фиксированным числом граней, называемые конечными элементами. На практике генерация трехмерной конечноэлементной сетки является фундаментальной геометрической проблемой в применении МКЭ [1]. С проблемой генерации сетки тесно связана и проблема ввода и хранения геометрической формы исследуемых объектов, а во многих случаях еще и вывода результатов в графической форме. Естественным выбором сегодня является какая-либо САПР, которая могла бы взять на себя полное или частичное решение этих задач. Современный рынок программных продуктов предоставляет большое количество разнообразных по возможностям САПР [2]. Большинство из них, малые и средние САПР, обеспечивают только ввод-вывод и хранение геометрической и графической информации. В то же время предлагается и несколько «тяжелых» САПР (ANSYS™, EUCLID™, и др.) и несколько специализированных САПР (NASTRAN™, ABAQUS™ и др.), обладающих большими возможностями. Они позволяют выполнить три перечисленные задачи и, кроме того, провести численное моделирование в определенных рамках с помощью того же МКЭ. Понятно, что большие возможности этих программных пакетов имеют высокую стоимость, требуют мощную вычислительную технику и затраты на обучение. Не углубляясь в существо проблемы по приобретению готовых программных продуктов или созданию собственных, можно сказать, что проведенный анализ показывает, что большинство исследователей предпочитают разрабатывать собственные программы для решения своих задач. И авторы статьи, проводя исследования дисковых электрических машин с помощью МКЭ, пришли к необходимости разработки собственных про- грамм [3]. Разрабатывать программу ввода и хранения геометрической формы трехмерных объектов слишком сложно, да и нет необходимости. Проще и эффективней использовать готовую САПР. Поэтому данные задачи были возложены на Auto CAD 2000i™. Генератор же трехмерной конечноэлементной сетки был разработан авторами и написан на языке программирования С++. AutoCAD 2000i – САПР среднего класса, обладающая рядом существенных возможностей, среди которых развитые средства работы с твердотельными объектами и набор библиотек ObjectARX™. Библиотеки объектов и функций предоставляют полный доступ к внутренней структуре графических объектов и к внутренним функциям AutoCAD 2000i программных приложений, создаваемых с помощью Visual C++ 6.0™. Приложения работают в среде AutoCAD 2000i и могут быть очень мощными. Созданный с помощью этих пакетов генератор трехмерной треугольной сетки использует обсуждаемый далее алгоритм. Область исследования и разработки алгоритмов генерации двухмерных и трехмерных сеток является сегодня одной из самых динамичных и востребованных в численных методах математического моделирования. Постоянное развитие и совершенствование самих численных методов и расширение сферы их применения требует развития и разработки алгоритмов генерации сеток. В мире постоянно ведутся исследования в этой области. Разными исследователями (Vavasis, Mitchell, Eppstein, Bern и др.) уже разработаны алгоритмы [4], обладающие различными характеристиками, и выработаны критерии, которым должны удовлетворять алгоритмы. Наработанный материал позволяет сделать выбор основной идеи алгоритма и характеристик, которыми он должен обладать. Хотя в конечном итоге конкретная сфера и цель применения определяют необходимые требования к алгоритму и генерируемой сетке. В общем случае МКЭ позволяет решать задачи в двухмерной (2D) и трехмерной (3D) постановках. Использовать в нем можно прямолинейные и криволинейные конечные элементы. В двухмерных задачах применяются треугольники и четырехугольники, в трехмерных – тетраэдры, призмы и параллелепипеды. Кроме того, прямолинейные элементы всегда двухузловые, а криволинейные элементы могут быть трехузловыми и четырехузловыми (имеется в виду число узлов на каждом ребре). Несмотря на такое разнообразие элементов, чаще всего используются линейные треугольные элементы (в 3D постановке – тетраэдры). Их легче генерировать и использовать, ими можно хорошо дискретизировать криволинейные объекты вместо использования криволинейных элементов. В МКЭ генерация сетки является задачей, не зависимой от остальных процессов, и требования к быстродействию не столь высоки. Более важными являются характеристики генерируемой сетки конечных элементов и требования к геометрической форме исследуемых объектов. В связи с изложенным были выработаны требования, которым должен удовлетворять современный алгоритм генерации трехмерной конечноэлементной сетки. Прежде всего генератор должен обслуживать исследуемые объекты, обладающие следующими характеристиками: - объектов может быть несколько; - они должны быть трехмерными и твердотельными, то есть физические характеристики объекта предполагаются неизменными в любой точке объекта; - объекты могут быть произвольной формы – выпуклые и невыпуклые, содержать криволинейные поверхности и линии, иметь различные сквозные отверстия; - должно учитываться взаимное расположение объектов и их расположение относительно центра координат.
Сам алгоритм должен: использовать возможности САПР, в которой он будет работать и обеспечивать хорошее быстродействие. В основу алгоритма положена идея из [5], состоящая в том, чтобы разделить исследуемые объекты с помощью генерируемых кубов на множество компонентов, удовлетворяющих определенным требованиям, а затем эти компоненты разделить на тетраэдры (конечные элементы), которые и составят трехмерную треугольную сетку. Основной структурой данных алгоритма является восьмиричное дерево, состоящее из узлов. С каждым узлом связывается выпуклый многоугольник, представляющий собой трехмерный куб, пересекающий один из исследуемых объектов. Все кубы строго ориентированы по осям общей системы координат. Каждый узел дерева может быть либо концевой вершиной, либо содержащим восемь узлов-потомков. Укладка из восьми потомков представляет собой восемь кубов, занимающих тот же объем. Логически эта укладка получается с помощью деления куба владельца пополам по каждому измерению. Любой из узлов-потомков также может быть либо концевой вершиной либо укладкой из восьми своих потомков. Узел может содержать список узлов-дубликатов.
Для функционирования алгоритма важны еще две категории узлов. Соседними называются узлы, кубы которых имеют хотя бы одну общую точку. Примыкающими называются соседние узлы, компоненты пересечения которых имеют хотя бы одну общую точку. Таким образом, первая фаза алгоритма генерации трехмерной сетки выглядит следующим образом. Для начала необходимо указать объекты, которые будут исследоваться. Используя размеры и положение выбранных объектов, определяют размер и положение первого куба, который должен охватывать собой эти объекты. Первый куб является и первым узлом восьмиричного дерева. Начиная с этого узла, генерируется дерево. На каждом шаге генерации дерева находится пересечение куба данного узла с исследуемыми объектами, при необходимости узел дублируется и делится. Процесс рекурсивно продолжается до тех пор, пока все концевые вершины не станут защищенными узлами. Защищенным называется узел, содержащий простой компонент, который не нужно делить. Узел, не пересекающий ни одного объекта, удаляется из дерева. В процессе генерации дерева каждый узел делится, если: - размер куба больше заданного максимального размера; - компонент пересечения не является простым компонентом; - компонент простой, но его центр масс находится за пределами самого компонента; - компонент простой, но узкий – центр масс куба не находится в пределах компонента; - компонент простой, но его грани содержат внутренние контуры; - размер куба больше размера линеаризации, при условии, что компонент простой и содержит криволинейные поверхности. Цель деления узлов и генерации дерева – разделить исследуемые объекты на малые и простые компоненты, которые затем было бы просто разделить на тетраэдры. Простыми компонентами называются компоненты пересечения какого-либо куба с исследуемыми объектами, удовлетворяющие следующим требованиям: - компонент равен кубу (рис. 2a); - внутри куба находится одна грань компонента (рис. 2b); - внутри куба находится одно ребро компонента и две образующие ребро грани (рис. 2e,d); - внутри куба находится одна вершина компонента и несколько образующих вершину граней (рис. 2f,g,h). Первая фаза алгоритма выглядит довольно простой, однако в ней есть несколько особенностей, порождающих большие последствия. Это связано с высокими требованиями, предъявляемыми к генерируемой сетке. Первой проблемой (и на это указывают исследователи [4,5]) является наличие у объектов криволинейных поверхностей. У многих исследователей она вызывает большие трудности, но в основном из-за того, что они одновременно решают задачу ввода и обработки геометрической формы объектов. В нашем случае проблема решена довольно легко введением размера линеаризации, который по сути является шагом дискретизации кривых линий. Так как всю работу с геометрической формой объектов берет на себя САПР, и структура алгоритма генерации тетраэдров из простых компонентов такова, что новые узлы не создаются, а используются только существующие вершины компонентов, на фазе деления объектов происходит автоматическая линеаризация кривых и поверхностей. Второй важной проблемой является коэффициент формы генерируемых тетраэдров. Тетраэдры не должны иметь очень острые углы и по форме должны быть как можно ближе к равносторонним тетраэдрам. Для МКЭ очень важно, чтобы сетка была сбалансированной. Качество конечных элементов и сбалансированность сетки очень сильно определяют качество дальнейших расчетов в МКЭ [1], особенно при необходимости добиться от метода высокой точности и сходимости. Сбалансированности генерируемой сетки можно достичь, если каждый узел в дереве будет удовлетворять условию баланса. Условие баланса. Каждый соседний узел непременно делится, если он больше данного узла более чем в два раза. Это условие можно ввести еще на стадии деления узлов, а можно оформить отдельной операцией после фазы деления. В результате в сетке не образуются «дыры» – большой тетраэдр, окруженный маленькими тетраэдрами. Коэффициент формы неявно учитывается во многих местах алгоритма. Это отказ от узких компонентов, выпуклость формы компонентов, близость формы компонентов к кубу. Учитывается он и на фазе генерации тетраэдров. На практике в связи с коэффициентом формы выявилась такая проблема, которая не обсуждается в литературе. Дело в том, что в процессе деления узлов могут появиться компоненты с гранями, контур которых невыпуклый (рис. 2e,g). В этих случаях грани трудно триангулировать. Генерируемые тетраэдры получаются острыми и не образуют форму исходного компонента. Усиленное деление такого узла не только измельчает сетку и перегружает алгоритм, но и не имеет полного эффекта. Такой узел остается, и его приходится каким-то образом «линеаризовать». Для этого необходимо выявить подобные узлы и разделить компоненты на выпуклые элементы, например, их внутренними плоскостями. Программная реализация первой фазы алгоритма не вызывает больших трудностей. Так, для генерации кубов, пересечения объектов, определения центров масс и выпуклости граней и других геометрических операций можно использовать библиотечные функции и объекты. Для определения простого компонента можно определять количество граней и вершин компонента, находящихся внутри куба, но не учитывать ребра. В этом случае компонент на рисунке 2c оказывается в группе с внутренним ребром, но это не оказывает никакого влияния на вторую фазу алгоритма. Вторая фаза алгоритма генерирует тетраэдры из простых компонентов, полученных в первой фазе. Суть этой фазы состоит в том, чтобы разделить каждую грань компонентов на плоские треугольники, а затем добавить к ним центры масс компонентов в качестве четвертой вершины. В результате получаются тетраэдры. Требований к треугольникам только два: они должны покрывать полностью всю грань и быть по форме близкими к равносторонним треугольникам. Если усиленно добиваться идеального коэффициента формы и для этого, проводя математические вычисления, добавлять новые вершины в компонент, то алгоритм станет сильно перегруженным. Быстродействие тоже является важной характеристикой алгоритма. Необходимо оптимальное решение. К тому же необходимо учесть, что в МКЭ не может быть независимой сетки для каждого исследуемого объекта, тем более если объекты соприкасаются и образуют границу раздела сред. Узлы, получаемые на такой границе, должны относиться к обоим объектам. При создании новых узлов их необходимо переносить и на компоненты соседних объектов. В силу этого целесообразней использовать только существующие вершины. Более того, следует еще привести в соответствие все существующие вершины на всех компонентах, чтобы в сетке не появились пробелы – области объектов, не занятые тетраэдрами. Для этого необходимо провести предварительную процедуру по добавлению вершин. Для каждого узла необходимо отыскать примыкающие узлы и добавить компоненту данного узла вершины компонента примыкающего узла, отсутствующие у первого. В этом случае сетка гарантирована от пробелов. Что касается триангуляции граней, то, как уже указывалось, наработаны алгоритмы двухмерной триангуляции плоских объектов, хотя и слишком общие для данной задачи. Для нашей задачи квалифицированный специалист может разработать свой алгоритм, более удовлетворяющий его. Авторы использовали два алгоритма. В одном берется центр грани и от него проводятся лучи ко всем вершинам. А во втором вершины обходятся по спирали и соединяются в треугольники. Разные алгоритмы использовались для различных узлов, с целью лучшего баланса сетки. На последнем этапе треугольники каждого компонента формируются в тетраэдры с помощью центра масс компонента. При этом следует учесть два момента. Во-первых, так как еще на этапе деления объектов проверяется условие нахождения центра масс в пределах компонента, то никаких неожиданностей с формированием тетраэдров не возникнет. Во-вторых, при формировании сетки из тетраэдров необходимо учитывать, что МКЭ использует не сами тетраэдры, а узлы сетки и, соответственно, глобальную нумерацию узлов сетки для всей группы исследуемых объектов. Нумерация узлов сетки – важный момент в применении МКЭ, от нее зависит разреженность глобальной матрицы уравнений. Поэтому необходимо реализовать либо отдельную процедуру нумерации, либо при формировании сетки сразу нумеровать узлы сетки. Таким образом, разработан практичный и простой в реализации алгоритм генерации трехмерной сетки. Основными достоинствами алгоритма являются: · отсутствие ограничений на геометрическую форму исследуемых объектов; · высокое качество генерируемой сетки элементов; · простота реализации. Алгоритм не отличается высоким быстродействием. Однако следует учитывать, что быстродействие программы зависит от производительности компьютера. Поэтому авторы не посчитали этот критерий столь существенным. Алгоритм опробован на практике и удовлетворяет сформулированным требованиям. Список литературы 1. Галлагер Р. Метод конечных элементов. Основы / Пер. с англ. - М.: Мир, 1984. - 428 с. 2. САПР и графика. - 1998-2001. 3. Чучалин А.И., Сипайлов Г.А., Горисев С.А., Шари- ков Ю.И. Математическое моделирование электромашинного импульсного генератора многодисковой конструкции. // Проблемы нелинейной электротехники: Тез. докл. III Всесоюз. науч.-техн. конф. 12–15 сентября 1988 г. - Ч. 2. - Киев, 1988. - С. 207–209. 4. Bern M. and Eppstein D. Mesh generation and opti- mal triangulation. - Computing in Euclidean Geometry, edited by F. K. Hwang and D.-Z. Du, World Scientific, 1992. (см. также Tech Report CSL-92-1, Xerox PARC, March, 1992). 5. Mitchell S. A. and Vavasis S. A. Quality mesh generation in three dimensions. - Proceedings of the Eighth Annual Symposium on Computational Geometry, 212-221, ACM Press, 1992. (см. также Cornell Theory Center Technical Report CTC92TR104). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=848 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
| Статья опубликована в выпуске журнала № 3 за 2001 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формулировка задачи планирования линейных и циклических участков кода
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- Сравнительный анализ некоторых алгоритмов распознавания
- Параллельная обработка в алгоритмах визуализации с трассировкой лучей
Назад, к списку статей



 Характеристики генерируемой сетки и элементов следующие: элементы должны быть тетраэдрами и обладать хорошим коэффициентом формы; сетка должна быть сбалансированной и единой для всей группы исследуемых объектов.
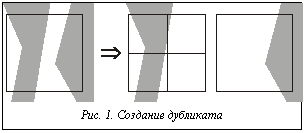
Характеристики генерируемой сетки и элементов следующие: элементы должны быть тетраэдрами и обладать хорошим коэффициентом формы; сетка должна быть сбалансированной и единой для всей группы исследуемых объектов.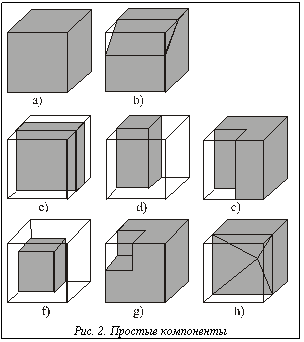 Каждый из узлов может быть дублирован несколькими узлами-дубликатами. Дубликат – это точная копия узла, которая создается всякий раз, когда пересечение куба основного узла с исследуемыми объектами имеет несколько отдельных компонентов. Такое возможно при наличии нескольких объектов исследования и отверстий в них. Каждый дубликат связан только с одним компонентом пересечения (рис. 1). При этом все дубликаты в алгоритме рассматриваются как самостоятельные узлы и также могут делиться.
Каждый из узлов может быть дублирован несколькими узлами-дубликатами. Дубликат – это точная копия узла, которая создается всякий раз, когда пересечение куба основного узла с исследуемыми объектами имеет несколько отдельных компонентов. Такое возможно при наличии нескольких объектов исследования и отверстий в них. Каждый дубликат связан только с одним компонентом пересечения (рис. 1). При этом все дубликаты в алгоритме рассматриваются как самостоятельные узлы и также могут делиться.