Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Дисковая сборка мусора с логическим делением пространства кучи
Аннотация:
Abstract:
| Автор: Козловский В.С. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10065 |
Версия для печати Выпуск в формате PDF (1.83Мб) |
Сборка мусора в оперативной памяти является широко изучаемой областью [1]. Для разных условий было предложено и исполнено множество алгоритмов, чего, однако, нельзя сказать о дисковой сборке мусора. Логичным кажется применение алгоритмов, разработанных для сборки мусора в основной памяти, но преобразованных к условиям долговременного хранения. Как показывают исследования, проведенные в области управления памятью в системах управления объектно-ориентированными БД, алгоритмы, хорошо зарекомендовавшие себя для языков программирования, фактически не применимы в отношении БД [2]. Причина этого в большом количестве различий между этими системами, например, наличие в СУБД транзакций, мультидоступа, долговременности и объемов данных, на порядки превышающих объемы, используемые большинством приложений. На работу дискового сборщика мусора влияют параметры, значение которых для обычных сборщиков может быть пренебрежимо мало. Так, например, время доступа к объекту на диске на несколько порядков больше, чем при обращении к объекту, резидентному в основной памяти. Простой способ сборки мусора состоит в трассировке всех объектов, достижимых из корневых указателей (root set), и затем следует учет и обработка неиспользуемого пространства. Однако трассировка глобального графа объектов в распределенной системе будет требовать кооперативной работы всех серверов, и все серверы должны закончить трассировку до начала сборки мусора. Подобный подход требует задержек в работе процессов (сервер должен ждать результатов работы других), а в случае возникновения сбоя на одном из серверов это ожидание может быть сколь угодно долгим. Как правило, дисковое пространство в сотни и более раз превышает объем имеющейся оперативной памяти. В случае трассировки всего объема дискового пространства одна и та же страница может загружаться в память и удаляться оттуда несколько раз, что замедляет проведение трассировки. А это приводит к необходимости проведения множества операций ввода/вывода и требует использования оперативной памяти, что отнимает ресурс, необходимый для исполнения приложениями.
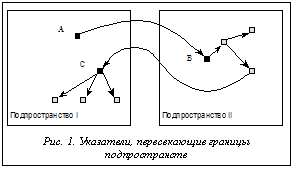
Для выполнения сборки мусора в подпространстве независимо от остальных подпространств сборщик запоминает объекты, на которые имеются ссылки извне, и использует их как корневые указатели. Набор таких указателей называется списком входящих ссылок подпространства. Каждый из входящих указателей обычно содержит ассоциированный с ним счетчик, содержащий число указателей на объект извне. Если значение счетчика уменьшается до нуля, соответствующий член списка исключается. Рассмотрим случай, когда по каким-либо причинам не удается использовать только одно подпространство для размещения объектов приложения (это значит, что будут существовать ссылки, пересекающие границы подпространств). Такая ситуация может возникнуть из-за недостаточного объема свободной памяти в пределах одного подпространства в случае неэффективного выделения свободных блоков по причине фрагментации памяти. Для проведения сборки учитывается набор входящих в подпространство ссылок, которые в этом случае считаются частью набора изначальных (корневых) указателей. Консервативность подхода в этом случае состоит в том, что все достижимые из входящих указателей объекты считаются живыми, то есть используемыми приложением, даже если некоторые из них не являются достижимыми из изначального набора. Для оценки объема памяти, который может быть удержан вследствие использования такой схемы логического разбиения диска, рассмотрим худший случай развития событий (рис. 1). По рисунку видно, что часть данных приложения с некоторого момента стала недоступна. Существуют ссылки, пересекающие границы подпространств. Очевидно, что пока объект А в подпространстве I не будет освобожден, ссылка из этого объекта будет рассматриваться как один из корневых указателей для подпространства II и все мусорные данные, достижимые из объекта А, будут считаться живыми, удерживая при этом дополнительный объем памяти. В свою очередь, объект С не может быть освобожден до освобождения объекта В и т.д. Оценим объем памяти, который будет необходим для работы приложения в системе с трассирующей сборкой мусора, исходя из предположения о наиболее длинной структуре данных приложения (части графа достижимости приложения с наиболее длинным путем), которая может стать мусором. В дальнейших рассуждениях предполагается определить дополнительный объем памяти, вносимый нециклическими структурами. С точки зрения занимаемого объема памяти любая структура данных может быть представлена как совокупность определенного количества ссылок, направленных извне подпространства, и объемов памяти, удерживаемых каждой такой ссылкой в пределах одного подпространства. Рисунок 2 иллюстрирует такое описание структуры данных приложения. Примем следующие обозначения: l – величина пути в графе достижимости структуры данных приложения, которая может стать мусором; mi – вес i-го узла рассматриваемой части графа. При этом 0
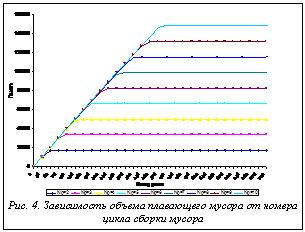
Попробуем оценить объем памяти, занимаемый плавающим мусором в зависимости от номера цикла сборки мусора, для нескольких подпространств. Для начала будем считать, что все указатели структуры данных пересекают границы подпространства, то есть р=1. Примем, что в рассматриваемом случае внешняя фрагментация отсутствует. На рисунке 3 показан случай для шести подпространств (Np=6), в которых расположена мусорная структура. Очевидно, что память, занимаемая мусорными объектами первой цепочки в первом подпространстве, будет освобождена не раньше чем сборщик произведет Np +1 сборку мусора. В приведенном примере это будет сборка под номером 7. Следующий раз для этой же мусорной структуры память будет освобождаться не ранее 12-го цикла, что соответствует 2 Np, далее не ранее цикла 22=3Np -1. Для второй цепочки сборки мусора будет аналогичная картина, но с запаздыванием на один цикл. В таблице 1 приведены номера циклов сборки, на которых осуществляется освобождение блоков памяти, для нескольких цепочек мусора.
Объем памяти
где n – номер цикла сборки. На рисунке 4 показаны зависимости объемов плавающего мусора (в Кб) от номера цикла сборки мусора с p = 0,1 для Np = 6. Графики строились с использованием следующих условий: mmin= 1Кб; N = 411;
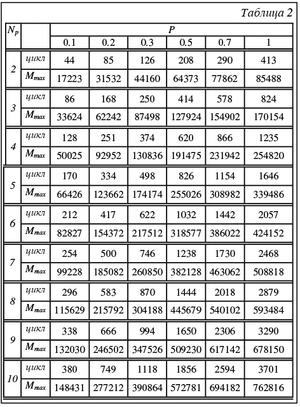
В таблице 2 приведены данные о номерах циклов, на которых происходит насыщение, и о максимальном объеме плавающего мусора (в Кб), рассчитанные с теми же исходными условиями для различных р и Np. Как видно из таблицы, значения номера цикла насыщения в лучшем из рассмотренных случаев р=0,1 и Np =2 и худшем из рассмотренных случаев р=1 и Np =10 различаются в 84 раза. А объемы памяти, занимаемые плавающим мусором, различаются в 44 раза для одного и того же приложения. Это говорит о необходимости применения способов, позволяющих локализовать указатели в пределах минимально возможного количества подпространств. Рассмотренный подход позволяет оценить потери памяти, которые могут возникнуть в ходе работы системы. На основе предварительных данных система может быть настроена на использование определенных приложений, которые могут различаться наборами характеристик, таких как структуры данных, объемы размещаемой памяти, связность графа достижимости. Верхняя граница объема используемой памяти, полученная на основе сведений о работе приложений и характеристиках системы, гарантированно не будет превышена. Существуют другие схемы выбора подпространства для выполнения текущего цикла сборки мусора, для каждой из которых необходимо рассмотреть наихудший случай исполнения. Приведенные рассуждения являются лишь частью работы по оценке наихудшего случая использования памяти. Необходимо также получить оценку работы применяемых алгоритмов сборки мусора и размещения новых блоков памяти. Для прогнозирования работы и конфигурации системы с учетом рационального использования ресурсов достаточно использовать результаты исследования исполнения сборки мусора в худшем случае. Список литературы 1. Richard Jones, Rafael Lins. Garbage collection: algorithms for automatic dynamic memory management. Chichester, England, John Wiley & Sons, 1996. 2. Jonathan E. Cook, Alexander L. Wolf, Benjamin G. Zorn, A Highly Effective Partition Selection Policy for Object Database Garbage Collection IEEE Transactions on knowledge and data engineering, Vol. 10, NO. 1, January/February 1998. 3. Andrew W. Appel Simple Generational Garbage Collection and Fast Allocation Department of [3]. Computer Science Princeton University, March 1988. 4. Barbara Liskov Umesh Maheshwari Tony Ng Partitioned Garbage Collection of a Large Stable Heap (Extended Abstract ) Published in the Proceedings of IWOOOS, October 1996 |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=906 |
Версия для печати Выпуск в формате PDF (1.83Мб) |
| Статья опубликована в выпуске журнала № 4 за 2000 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Алгоритмы и программное обеспечение системы обработки топопланов
- Реализация теней с помощью библиотеки OpenGL
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- Метод интегрированного описания топологических отношений в геоинформационных системах
- Инструментальные и программные средства построения сетевых моделей
Назад, к списку статей



 Опыт исследований сборки мусора в языках программирования показывает, что проведение сборки мусора в широких адресных пространствах может быть более эффективным, если сборку производить в частях пространства, где каждая часть может быть обработана независимо от других [3]. По этой причине во многих системах используется логическое деление кучи на подпространства. В настоящей статье речь идет о сборке в частях кучи (partitioned garbage collection) для системы, в которой кучей является область диска [4]. Для проведения одного цикла сборки мусора на диске целесообразно его разбить на части, которые называются подпространством. Преимущество разбиения на подпространства состоит в более компактном расположении указателей, уменьшается количество страничных операций ввода/вывода. Причем наблюдается уменьшение помех со стороны сборщика мусора другим процессам, протекающим на сервере.
Опыт исследований сборки мусора в языках программирования показывает, что проведение сборки мусора в широких адресных пространствах может быть более эффективным, если сборку производить в частях пространства, где каждая часть может быть обработана независимо от других [3]. По этой причине во многих системах используется логическое деление кучи на подпространства. В настоящей статье речь идет о сборке в частях кучи (partitioned garbage collection) для системы, в которой кучей является область диска [4]. Для проведения одного цикла сборки мусора на диске целесообразно его разбить на части, которые называются подпространством. Преимущество разбиения на подпространства состоит в более компактном расположении указателей, уменьшается количество страничных операций ввода/вывода. Причем наблюдается уменьшение помех со стороны сборщика мусора другим процессам, протекающим на сервере.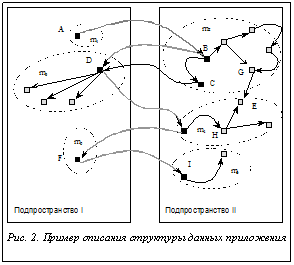 Рассмотрим общий случай, когда существуют ссылки, пересекающие границы нескольких подпространств. На рисунке 3 представлена ситуация, когда в мусорных объектах существуют ссылки, пересекающие границы нескольких подпространств. В худшем случае цепочки мусора будут равномерно распределены между подпространствами, и направление ссылок будет противоположно перемещению работы сборщика мусора. Затемненными областями на рисунке показаны подпространства, где производится сборка мусора. Через Np обозначим количество подпространств, в которых может располагаться цепочка мусора. В худшем случае цепочка плавающего мусора образуется в том подпространстве, в котором производится сборка мусора. Если сборщик мусора вызывается для всех подпространств последовательно, это значит, что он доберется до головы цепочки только после обработки всех остальных подпространств, сделав полный круг.
Рассмотрим общий случай, когда существуют ссылки, пересекающие границы нескольких подпространств. На рисунке 3 представлена ситуация, когда в мусорных объектах существуют ссылки, пересекающие границы нескольких подпространств. В худшем случае цепочки мусора будут равномерно распределены между подпространствами, и направление ссылок будет противоположно перемещению работы сборщика мусора. Затемненными областями на рисунке показаны подпространства, где производится сборка мусора. Через Np обозначим количество подпространств, в которых может располагаться цепочка мусора. В худшем случае цепочка плавающего мусора образуется в том подпространстве, в котором производится сборка мусора. Если сборщик мусора вызывается для всех подпространств последовательно, это значит, что он доберется до головы цепочки только после обработки всех остальных подпространств, сделав полный круг.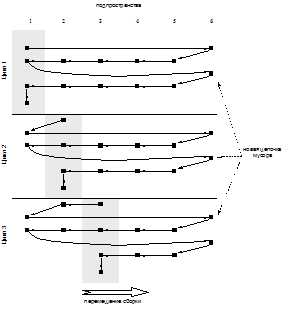
 Отметим, что память, освобожденная на n цикле, может быть использована заново только на n+1 цикле. Можно выделить три стадии работы системы: сборка мусора не приводит к освобождению блоков; освобождается и используется заново часть требуемых блоков; памяти освобождается достаточно для размещения любой структуры данных приложения.
Отметим, что память, освобожденная на n цикле, может быть использована заново только на n+1 цикле. Можно выделить три стадии работы системы: сборка мусора не приводит к освобождению блоков; освобождается и используется заново часть требуемых блоков; памяти освобождается достаточно для размещения любой структуры данных приложения.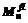 , занимаемый плавающим мусором, для рассматриваемого случая на n-м шаге можно подсчитать с использованием следующих формул.
, занимаемый плавающим мусором, для рассматриваемого случая на n-м шаге можно подсчитать с использованием следующих формул.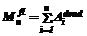 ,
, 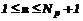 ;
;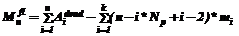 ,
,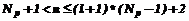 ;
; 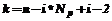 ;
; 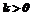
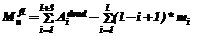 ,
,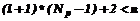 ;
;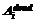 = 411.
= 411.