Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (byg@yandex.ru) - , Ph.D, Dli M.I. (midli@mail.ru) - (Smolensk Branch of the Moscow Power Engineering Institute, Smolensk, Russia, Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 8123 |
Print version Full issue in PDF (1.58Mb) |
Авторами в ряде работ [1,2] было введено понятие локально-аппроксимационных, или программных моделей. В настоящей статье рассмотрены точностные характеристики таких моделей применительно к задаче моделирования многофакторных статических объектов. Приведем вначале описание алгоритма моделирования. Предположим, что исследуемый статический объект имеет n входов (иначе – векторный вход Х) и один выход y и имеет истинное описание
где j(X) – функция неизвестного вида; e – аддитивная случайная помеха (отражающая действие неучитываемых факторов) с нулевым средним значением и произвольным (неизвестным) распределением на (-em, em). Предположим, далее, что на объекте может быть организован эксперимент, заключающийся в регистрации NЭ пар значений < Xi, yi >. Алгоритм построения локально-аппроксимационной (программной) модели может быть описан следующим образом. 1. Осуществляется нормировка значений входных факторов так, чтобы областью их определения стал единичный гиперкуб. 2. Из N (n+1£N составляется начальная база модели, отображаемая матрицей U 3. Для каждой новой экспериментальной точки производится нормировка элементов Х и (для нормированных значений) формируется вектор расстояний, например евклидовых или Хэмминга с элементами
4. Создается матрица D 5. Осуществляется сортировка строк данной матрицы по элементам 1-го столбца в порядке возрастания его элементов. 6. М первых (верхних) строк переформированной отмеченным образом матрицы D (значение М устанавливается заранее) используются для формирования матрицы F и вектора y: F 7. Рассчитывается прогнозируемое значение
8. Проверяется неравенство
где d – заданная константа, определяющая точность модели. При выполнении неравенства база данных модели пополняется путем расширения матрицы U (добавлением строки . В противном случае матрица U остается без изменений. 9. Проверяется правило останова. В качестве такого правила можно принять, например, перебор всех NЭ экспериментальных точек. Если не все экспериментальные точки использованы, то переход к п.3, в противном случае – окончание процедуры. При использовании модели заданными считаются сформированная матрица U – база данных модели (на этапе использования она не изменяется), отмеченные параметры М и d, и расчет Отметим, что возможны различные модификации рассмотренной процедуры. Точность моделирования устанавливается рядом теорем, которые для простоты приведем для двухмерного случая (n=2), при значении параметра M=n+1 и без доказательств. Теорема 1. Если шум наблюдений отсутствует (e º 0), а j(x1,x2) имеет вид квадратичного полинома, то систематическая ошибка модели не будет превышать заданного значения d, если точки Xi базы данных модели образуют на единичном квадрате регулярную решетку, такую, что три ее ближайших узла являются вершинами равностороннего треугольника с длиной стороны
где В – матрица двух производных функции j(×). На рисунке изображено оптимальное размещение точек базы данных линейной локально-аппроксимационной модели при n=2 и M=3. Теорема 2. Если e º 0, а функция j(Х) представляет собой на единичном квадрате, по крайней мере, дважды дифференцируемую функцию по каждому из аргументов, а Xi являются случайными величинами с плотностью вероятности f(X)>0, то систематическая погрешность модели (2), (3) стремится к нулю при N®¥ с вероятностью 1. Следствие. Если j(X) есть квадратичный полином и выполняются условия теоремы 2, то оптимальной плотностью вероятности (на единичном квадрате) в смысле скорости сходимости процедуры построения модели является f(X) = 1, (6) иначе говоря, в этом случае точки Xi должны чисто случайно разбрасываться в единичном квадрате. Теорема 3. Если функция j(X)=j(x1,x2) на единичном квадрате удовлетворяет дифференциальному уравнению
и частные производные в правой части (7) неотрицательны, то оптимальная плотность вероятности f(X) где D0=const – нормируемый множитель. Результаты данной теоремы применимы, если априори известно, что функция j(×) принимает наибольшее (наименьшее) значение в одной из угловых точек единичного квадрата. Приведенные результаты допускают обобщение на многомерный случай. Можно показать также, что при e¹0 и eÎ(-em, em) случайная погрешность модели не превосходит величины 2em. Изложенное позволяет выработать рекомендации по выбору параметров M и d алгоритма моделирования и организации идентифицирующего (обучающего) эксперимента. Список литературы 1. Дли М.И. Программные модели сложных объектов. – Смоленск, 1998. (Препр. МЭИ, филиал в Смоленске). 2. Дли М.И., Круглов В.В. Применение метода локальной аппроксимации при построении алгоритмических моделей объектов управления// Вестн. МЭИ. - 1998. - № 6. - С.109-111. |
| Permanent link: http://swsys.ru/index.php?page=article&id=938&lang=en |
Print version Full issue in PDF (1.58Mb) |
| The article was published in issue no. № 2, 1999 |
Perhaps, you might be interested in the following articles of similar topics:
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Инструментальные и программные средства построения сетевых моделей
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
Back to the list of articles
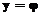 (Х) + e, (1)
(Х) + e, (1)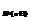 со строками вида >.
со строками вида >. , i=1,2,...,N.
, i=1,2,...,N.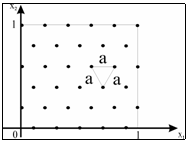 Если точка Х совпадает с какой-либо Xi из имеющихся в базе данных, то матрица U модифицируется заменой yi на
Если точка Х совпадает с какой-либо Xi из имеющихся в базе данных, то матрица U модифицируется заменой yi на 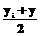 ; переход к началу п.3, в противном случае – переход к следующему пункту.
; переход к началу п.3, в противном случае – переход к следующему пункту. , образованная строками >.
, образованная строками >. Y
Y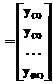 . (2)
. (2)
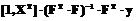 . (3)
. (3)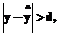 (4)
(4) производится в соответствии с п.п. 3-7 приведенного алгоритма.
производится в соответствии с п.п. 3-7 приведенного алгоритма.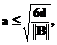 (5)
(5)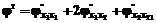 (7)
(7)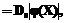 (8)
(8)