Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Проблемы кибернетики: свобода и организованность в универсальных системах
Аннотация:
Abstract:
| Автор: Тимофеев В.К. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 9326 |
Версия для печати Выпуск в формате PDF (1.07Мб) |
Междисциплинарные исследования на стыке наук способствуют созданию интеллектуальных продуктов для приоритетного использования их в социальной, экономической и политической деятельности, позволяют обеспечить синтез наукоемких технологий универсальных технических, управленческих и других развивающихся и самоорганизующихся систем. Работа направлена на поиск фундаментальных закономерностей и оптимальных параметров в базовых конструкциях универсальных быстродействующих суперЭВМ. Из теории информации известно, что максимальное количество информации численно равно максимальному значению энтропии, что энтропию можно определить как меру неопределенности или как меру разнообразия возможных состояний системы. Энтропия дискретного источника равна H(X)=SUM(P(Xi)*LOG(1/P(Xi))), где P(Xi) – вероятность событий. Используя приведенное соотношение, можно раскрыть существо названной проблемы. Основным свойством универсальной высокопроизводительной вычислительной системы предлагается считать выполнение ею максимального количества функций заданным количеством логического оборудования. К настоящему времени накопился достаточный опыт широкого применения так называемого до сих пор эмпирического соотношения Рента при разработке и решении различных задач проектирования высокопроизводительных вычислительных систем. В 1987 г. Б.Н.Файзулаев и П.Л.Барсегян раскрыли физический смысл показателя Рента: Р=1–LOG (H)/LOG (N), где H – логическая глубина конструктива или всей машины; N – общее число интегральных схем конструктива или машины в целом. Как видно из этого выражения, показатель Рента, характеризующий быстродействие архитектуры схемы, однозначно определяется средней глубиной логических цепей Н и лежит в диапазоне 0 Предельному случаю параллелизма обработки (при Н=1) соответствует Р=1 (так как LOG(1)=0) и наоборот, случаю предельно последовательной обработки информации (H=N) соответствует показатель Рента Р=0. Для большинства высокопроизводительных ЭВМ общего назначения показатель Рента находится в пределах P=0.4–75. В то же время он является основным элементом фундаментальных соотношений в базовых конструктивах ЭВМ. С его помощью может быть определено около двух десятков конструктивных параметров ЭВМ. В связи с этим очень важно найти единственное значение показателя Рента для универсальных машин, поскольку превышение значения показателя Рента блока над средним значением показателя Рента ИС приведет к избыточному количеству контактов соединителей, к завышенной длине связей (Lср, Lmax), увеличению размеров блока и т.д. Превышение среднего значения показателя Рента интегральных схем над показателем Рента блока приведет к снижению коэффициента использования ИС, повышению потребляемой мощности и пр. Предлагается обратить внимание на то, что по существу в формуле Файзулаева мы имеем право рассматривать отношение LOG(H)/LOG(N) как отношение количественной характеристики макромодели к аналогичной характеристике микромодели, хорошо известной в статистической части Второго закона термодинамики Р=1–LOG(H)/LOG(N)=1–K*LOG(H)/ /(K*LOG(N))=1–HT /HM=1–Hотн, где К – постоянная Больцмана; НТ – текущее значение энтропии; HM – максимальное значение энтропии, хаос, максимальная свобода, полное отсутствие взаимосвязи между элементами; Нотн – относительная энтропия, свободная часть многоэлементной системы. Можно записать: Р+Нотн=1. Рассмотрим физическую суть изложенных понятий. Представим себе, что полное число N элементов определяет максимальное значение энтропии Hт = LOG(N). Если некоторые из них взаимосвязаны, то система описывается формулой Шеннона-Больцмана и показывает новое (текущее) значение энтропии, которое оказывается меньше максимального значения
После нормирования по максимальному значению энтропии 1=Нт/Нm+Re/Hm; 1=Hотн+Rотн. Отсюда организованность системы равна Rотн=1–Нотн. В этом выражении единица характеризует систему в целом. Следовательно, можно утверждать, что любая многоэлементная система состоит из свободы (Нотн) и организованности (Rотн). Таким образом, фундаментальное соотношение для систем любой физической природы Rотн=1–Нотн, показывающее, что организованность любой системы однозначно определяется относительной энтропией системы, что полная система содержит конкретную долю свободы и вместе с Р, являющимся дополнением до 1, теперь можно говорить не о показателе Рента, а о показателе организованности любой системы, поскольку новый показатель Р получен с использованием элементов Второго закона термодинамики, являющегося феноменологическим законом, его действия распространяются на любые системы независимо от их физической природы. Последнее утверждение (на данном этапе предположительно) позволяет нам использовать статистические процессы, рассматриваемые в газовой динамике, в частности распределение Максвелла-Больцмана при разработке ЭВМ. Важнейшей особенностью указанного распределения является то, что в хаотическом тепловом процессе содержится строгая закономерность: наибольшая крутизна изменения концентрации молекул (максимум производной функции распределения спектральной плотности вероятности) по скорости может быть строго определена. В то же время этой точке соответствует максимальное разнообразие (различие) концентраций на каждый дискрет скорости. Это разнообразие может быть некоторым образом преобразовано в свойство системы выполнить максимальное количество функций имеющимися средствами, то есть точка с максимальной крутизной характеризует систему как универсальную. Известно, что интеграл функции плотности вероятности в конечных пределах от а до b представляет собой численное значение относительной энтропии, поскольку интеграл от нуля до бесконечности равен 1. Наибольшее значение относительной энтропии в области положительных значений производной распределения Максвелла-Больцмана равно 0.43. Эта величина представляет собой максимально допустимую величину свободы развивающейся системы, то есть системы с жизнеспособным поведением. Увеличение свободы сверх этой величины переводит систему в область разрушения. Важно понимать, что в подобных системах упорядоченность (Rотн=1–Нотн= =0,57) превышает свободу Нотн=0.43. Граничными значениями относительной энтропии любой системы являются 0 и 1. Нам бы хотелось в этом интервале найти единственное (наилучшее) значение Нотн. Для этого необходимо предъявить системе дополнительное требование, так как неопределенность в указанном интервале иначе не может быть раскрыта. Пусть этим требованием будет одно из важнейших общественно полезных свойств системы: согласованность, эффективность, универсальность и др. Остановимся на последнем. Будем понимать под универсальностью способность системы выполнять максимальное количество функций (положительных действий) имеющимися средствами (оборудованием). В то же время отношение числа выполняемых функций к количеству используемого оборудования, с помощью которого эти функции выполняются, представляет собой производную некоторой математической зависимости. Наша задача состоит в поиске этой зависимости для интересующей нас системы. Более того, указанная зависимость должна позволить нам определить по ней значение относительной энтропии в окрестности точки с максимальным значением производной. Что известно о подобных системах? Следует обратить внимание на недавно (1993 г.) появившуюся новую науку – технетику. Основу ее составляет выявленная закономерность видового распределения в технических системах, имеющих гиперболическую зависимость, аналогичную той, которая хорошо изучена в биологических системах. В монографии [1] проводится анализ более 500 систем в технической и иных сферах человеческой деятельности. В этой работе выделены технические и информационные ценозы – новый класс систем, открыт закон информационного отбора и сформулированы основы науки, которая для технической реальности будет играть роль, аналогичную биологии для органического мира. Дальнейшее развитие указанных закономерностей, то есть представление их в виде распределения плотности вероятности, открывает путь к фундаментальным физико-математическим методам анализа статистических процессов и систем. Наша цель состоит в доказательстве соответствия последних распределению Максвелла-Больцмана. Перевод статистических данных в [1] подтверждает это предположение. В распределении Максвелла-Больцмана может быть найдено предельное значение производной. Этой точке соответствует максимальное разнообразие системы и наивысшая степень ее универсальности. Очень важно рассмотреть эту область с точки зрения использования полиномов Чебышева 1-го и 2-го рода К-го порядка, поскольку они, в свою очередь, обладают уникальными свойствами: имеют максимальную из известных в математике крутизну рабочей характеристики при заданном (выбранном) количестве элементов системы. Это свойство позволит осуществить принцип реализации максимально возможного положительного эффекта на единицу затрат ресурсов. В итоге для универсальных систем следует взять столь же универсальное значение относительной энтропии, полученное на основе анализа процессов газовой динамики, и определить основные конструктивные параметры универсальной ЭВМ. Аналогичным образом может быть раскрыта неопределенность во множестве иных технических, экономических, социально-политических и других систем, поскольку принцип реализации системой наибольшего количества выполняемых функций (положительных результатов) заданным количеством оборудования (ресурсов) представляет собой, по-видимому, самое важное свойство систем с жизнеспособным поведением и универсальных систем любой физической природы. Список литературы 1. Кудрин Б.И. Введение в технетику. - Томск, 1993. 2. Тимофеев В.К. Власть–Бизнес–Общество – взаимоотношения // журн. Междунар. фонда экономич. и социальн. реформ. // Реформа. – 1996.- № 1. 3. V. Timofeev. Power–Business–Society – Relations. // International Foundation for Economic and Social Reforms. // Reforma. - № 1, 1996. 4. Тимофеев В.К. Общенациональная идея: свобода + организованность. // журн. Междунар. фонда экономич. и социальн. реформ. // Реформа. – 1996.- № 6. 5. V. Timofeev. National Idea: Freedom + Self-Discipline. // International Foundation for Economic and Social Reforms. // Reforma. - № 6, 1996. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=941 |
Версия для печати Выпуск в формате PDF (1.07Мб) |
| Статья опубликована в выпуске журнала № 3 за 1999 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Место XML-технологий в среде современных информационных технологий
- Компьютер - хранитель домашнего очага
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля
- Автоматизированная информационная система маркетолога
- Метод интегрированного описания топологических отношений в геоинформационных системах
Назад, к списку статей



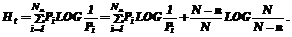 А собственно величина уменьшения есть показатель организованности, выраженный в тех же единицах, что и значение энтропии. Итак, Нm=Нт+Re, где Нm – максимальное значение энтропии; Нт – текущее значение энтропии; Re – показатель организованности.
А собственно величина уменьшения есть показатель организованности, выраженный в тех же единицах, что и значение энтропии. Итак, Нm=Нт+Re, где Нm – максимальное значение энтропии; Нт – текущее значение энтропии; Re – показатель организованности.