Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм визуализации трехмерных данных, заданных поверхностями свободных форм
Аннотация:
Abstract:
| Авторы: Долговесов Б.С. (bsd@iae.nsk.su ) - Институт автоматики и электрометрии СО РАН, лаборатория синтезирующих систем визуализации (зав. лабораторией), Новосибирск, Россия, кандидат технических наук, Чижик С.Е. () - , Вяткин С.И. (sivser@mail.ru) - Институт автоматики и электрометрии СО РАН, лаборатория синтезирующих систем визуализации (старший научный сотрудник), Новосибирск, Россия, кандидат технических наук, Есин А.В. () - , Жигач А.А. () - , Щербаков Р.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15442 |
Версия для печати Выпуск в формате PDF (1.07Мб) |
Компьютерная графика реального времени, ориентированная на визуализацию трехмерных сцен, достигла существенных успехов. Она находит широкое применение как в сложных системах визуализации для тренажерных комплексов (авиационных, космических, морских, автомобильных и т.п.), так и в графических акселераторах, используемых в компьютерных играх. В основе этих систем лежит полигональное задание объектов и трехмерных сцен с последующим преобразованием и сканированием в плоскости изображений. И хотя достигнута достаточно высокая степень достоверности отображаемых сцен в реальном времени, существует ряд задач, например отображение больших районов местности, где требуется хранить и отображать сцены, содержащие существенно большее число полигонов, чем реализовано в современных системах. Так, задача отображения горных районов местности требует для исходного описания сотни тысяч полигонов. Кроме этого, cуществуют специфические задачи в тренажеростроении, такие как задача динамической коррекции дисторсии, возникающей при проецировании изображения на криволинейные экраны с учетом подвижности наблюдателя и проектора, которая приводит к существенному увеличению количества полигонов. В работах [1-5] исследуются функциональные способы описания визуализируемых объектов, позволяющие существенно (в сравнении с полигональным заданием) сократить объем баз данных для определенного класса объектов. Однако отображение в реальном времени объектов, заданных таким способом, связано с существенным ростом требуемых вычислений из-за высокого порядка описывающих функций. С другой стороны, все большая потребность возникает в визуализации внутренних структур объектов. Отображение захода самолета в облачность в тренажерных задачах, визуализация данных, полученных в результате томографического сканирования объектов, требует визуализации объемов. Аналогичные задачи возникают в научной визуализации. В последнем проекте под названием Volumizer компания Silicon Graphics расширила API-стандарт введением объемных элементов изображения – вокселей, ограниченных четырьмя треугольными гранями – тетраэдрами. С целью визуализации воксельных объемов в реальном времени в последнее время предпринимаются попытки создания специальной аппаратуры. Так, компанией Mitsubishi Electronic разработана заказная СБИС vg500 [6] системы объемной визуализации VolumePro производительностью 500 миллионов вокселей в секунду, что позволяет визуализировать объем с разрешением 256´256´256 в реальном времени (30 Гц). В компании Hewlett Packard разработан метод визуализации объема через Фурье-преобразование [7]. Этот метод использует не пространственное описание объектов, а их частотные спектры. Это быстрый метод, однако его применимость ограничена простыми интегральными проекциями. Очень перспективный метод использует вейвлетное преобразование (wavelet transforms) [8]. Эти методы относятся к подходу на основе преобразования, в котором создается мультимасштабное представление объектов, что позволяет очень сильно сократить количество исходных данных и время вычислений. В данной работе приводятся результаты некоторых исследований по моделированию системы, в которой наряду с полигональным предлагается использование задания объектов поверхностями свободных форм в виде вещественных и скалярных функций и объемных областей воксельных массивов. Исследована возможность визуализации объемов, ограниченных поверхностями свободных форм. Для визуализации предлагается использовать рекурсивный алгоритм растрирования с делением объектного пространства и многоуровневым маскированием с учетом перспективы. Способы задания поверхностей Характерной особенностью предлагаемых способов задания поверхностей, во-первых, является то, что основными примитивами выбраны поверхности второго порядка – квадрики. На этой базе строится первый класс свободных форм с использованием вещественных функций. Поверхности такого типа выгодно применять при синтезе искусственных (рукотворных) объектов. Во-вторых, предлагается второй класс свободных форм с использованием скалярных функций возмущения относительно базовой поверхности, например для генерации рельефа местности или скульптурных моделей. Функции возмущения в неявном виде. Предлагается описывать сложные геометрические объекты, задавая функцию отклонения (второго порядка) от базовой поверхности тоже второго порядка. В простейшем случае F(x,y,z) задает поверхность второго порядка: F(x,y,z)=Ax2+By2+Cz2+Dxy+Exz+Fyz+Gx+ +Hy +Iz+K=0. На базе квадриков строятся поверхности свободной формы – композиция базовой поверхности квадрика и возмущения F’(x,y,z)=F(x,y,z)+R(x,y,z), где функция возмущения R(x,y,z) находится следующим образом:
где Q(x,y,z) – возмущающий квадрик. В качестве Q также может быть возмущенный квадрик (поверхность свободной формы). Другими словами, композиция базовой поверхности и функции отклонения является новой функцией возмущения, то есть производной для другой базовой поверхности. Получающаяся поверхность будет гладкой, и потребуется небольшое количество функций возмущения для создания сложных форм поверхностей. Таким образом, задача конструирования объекта сводится к задаче деформации поверхности квадрика нужным образом, а не к аппроксимации его примитивами (полигонами или патчами, представленными B-сплайновыми поверхностями). Функции возмущения в скалярном виде. Предлагается описывать сложные геометрические объекты, задавая функцию отклонения в скалярном виде от базовой поверхности второго порядка или в простейшем виде от базовой плоскости. Рельеф местности является частным случаем таких объектов и задается с помощью базовой плоскости и функции возмущения, которая определена в бесконечно длинном параллелепипеде. Значения функции возмущения задаются в поперечном сечении параллелепипеда двухмерной таблицей высот. В качестве базовой поверхности можно использовать плоскость, тогда направление нормали несущей плоскости должно совпадать с продольным направлением параллелепипеда – области определения функции возмущения. Поскольку во время растризации необходимо оценивать максимум функции на трехмерном или одномерном интервале, то для эффективности вычислений предварительно составляются карты уровней детальности. Исходные данные составляют уровень n, если размерность сетки равна 2n´2n. Данные для уровня n–1 получаются выбором максимума из четырех смежных значений уровня n, остальные три далее не учитываются, то есть получаем размерность сетки 2n-1´2n-1. Уровень 0 состоит из единственного значения – максимума по всей карте высот. При определении максимума возмущения вычисляется характерный размер проекции текущего интервала, исходя из которого выбирается уровень детальности. Для большего интервала выбирается более грубое приближение исходной функции. Если требуется более точное представление, чем имеется в наличии, то производится билинейная или бикубическая интерполяция значений высот, составляющих последний уровень детальности. Задание массивов вокселей. Все более широкое распространение получают сегодня методы визуализации внутренних структур объектов. Традиционная 3D графика основывается на представлении объектов поверхностями, как правило, полигональными. Существует представление объектов в виде объемов. Объем – это трехмерный массив кубических элементов (вокселей), представляющих единицы 3D пространства по аналогии с двухмерным массивом пикселей, каждый из которых представляет единицу площади. Массив вокселей, описывающий некоторый объект, можно рассматривать как трехмерную текстуру, хранящуюся в собственной системе координат. Несмотря на недостатки, связанные с большим количеством вычислений, объемное представление имеет очень важные достоинства: оно позволяет визуализировать внутренность объекта, а не только внешний слой, при этом, рендеринг и обработка зависят не от сложности объектов, а только от разрешения в трехмерном пространстве. Эти методы компьютерной графики называются визуализацией объема. Возможны два метода визуализации объема. 1. Объемные массивы вокселей генерируются в процессе сканирования из трехмерной карты плотности. При этом прозрачность элементов изображения выбирается в зависимости от значения плотности, а нормаль к изоповерхности (которая нужна для модели освещения) вычисляется как градиент плотнос- ти [9]. 2. Объемные массивы вокселей генерируются аналогичным образом, но до процесса визуализации. Преимущество этого подхода в том, что резко сокращаются вычислительные затраты. Для того чтобы вычислить вектор нормали к поверхности из дискретной сетки плотностей, требуется несколько операций сложения и умножения и, что самое главное, полученный вектор необходимо нормализовать, для этого требуется операция вычисления квадратного корня и деления. Если нормаль вычислена заранее, то в процессе визуализации нужно только перевести нормаль из текстурной системы координат в объектную, что делается соответствующей матрицей поворота. К недостаткам данного подхода следует отнести увеличение объема памяти для хранения текстуры. Трехмерную текстуру можно рассматривать как отдельный объект. Нанесение текстуры на объект можно интерпретировать как пересечение данного объекта с объектом-текстурой, при этом цвет и непрозрачность выбираются не из атрибутов объекта, а из текстурной карты. В данном подходе возможна комбинация объектов, заданных поверхностями и воксельными объемами, в случае когда объекты являются полупрозрачными, поверхности свободных форм могут использоваться как ограничивающие оболочки для трехмерной текстуры. При визуализации массивов вокселей, с целью повышения эффективности работы алгоритма растрирования иногда используют ограничивающие оболочки (как правило, в качестве ее берут выпуклый многогранник) [10]. Эффективность алгоритма сканирования будет определяться плотностью подгонки оболочки к объемным данным. Предлагаемый способ задания поверхностей как нельзя лучше подходит для решения данной проблемы. Поверхности свободных форм, способы задания которых были описаны выше, используются как ограничивающие оболочки для трехмерной текстуры. Кроме того, ограничивающие оболочки необходимы для реализации объемных теоретико-множественных операций [11] и для эффективной обработки объемных данных. Способ растризации Существует несколько способов сканирования при визуализации объема: растризация полигонов в пространстве экрана (визуальный образ объемных данных строится путем рендеринга полигонов: произведя рендеринг полигонов в порядке от заднего плана к переднему и смешивая их в буфере кадра, получают изображение объема); рендеринг в объектном пространстве, или рендеринг прямого хода (к этому способу относятся алгоритмы множественных преобразований [12,13], алгоритмы сплатинга [14-16], сдвиговые алгоритмы [17,18]); рендеринг обратного хода (к этому способу относятся алгоритмы трассировки [19] и отслеживания лучей [20-23]); гибридные способы, например, обратное инкрементальное преобразование в объектное пространство реализовано на IBM Power Visualization Sys- tem (PVS) [24]. В данной работе предлагается использовать алгоритм многоуровневого отслеживания лучей (multi-level ray casting) [25], осуществляющий эффективный поиск элементов объема – вокселей, участвующих в формировании изображения. Отличием алгоритма отслеживания лучей (ray casting) от трассировки лучей (ray tracing) является то, что в первом из них в целях увеличения скорости вычислений не отслеживаются вторичные лучи. Поиск производится в пространстве внутри куба от –1 до +1 по каждой координате, так что центр куба соответствует началу координат. На первом шаге рекурсии исходный объем разбивается на четыре меньших объема в экранной плоскости. Для каждого нового объема выполняется тест на пересечение с объектом. Если пересечение имеет место, то объем подвергается следующему уровню рекурсии. Объемы, не пересекающиеся с объектом, дальнейшему погружению в рекурсию не подлежат, что соответствует исключению из рассмотрения квадратных областей экрана, на которые данный объем (следовательно, и поверхность объекта) не отображается. Деление объема ведется до тех пор, пока его размер не станет равным размеру воксела (то есть достигается максимально возможный уровень рекурсии). Преимущество этой методики в том, что она позволяет на ранней стадии отбросить большие части пустого пространства. В процессе поиска вокселей, содержащих в себе участки поверхности объекта, формирующие изображение, осуществляется обход кубического пространства по четверичному дереву, листья которого являются корнями двоичных деревьев. В процессе обхода дерева используется механизм многоуровневого маскирования в случае непрозрачных объектов. Метод многоуровневого отслеживания лучей позволяет эффективно и быстро определить принадлежность лучей разных уровней (пирамид) поверхностям и отбраковать области пространства вне объектов. Наиболее просто деление пространства осуществляется в кубе или параллелепипеде. Однако при переходе к пирамидальному пространству (с учетом перспективы) можно столкнуться с проблемами либо увеличения порядка поверхностей, следовательно, сложности и количества вычислений, либо неоднородности пространственного описания элементов изображения (вокселей, воксельных объемов). Эти проблемы еще более усложняются при решении задачи компенсации дисторсии (каждый пространственный элемент изображения становится уникальным, что также затрудняет качественную фильтрацию). Решена задача простого (как в кубе) деления перспективного пространства (при этом пирамидальное пространство может быть достаточно произвольной формы, что очень важно для компенсации дисторсии) без увеличения порядка поверхностей за счет трансформации пространства в пространство. Применение проективного преобразования обобщает приведенный алгоритм на пирамидальные объемы, что позволяет синтезировать изображения с перспективой. В трехмерном пространстве точке с декартовыми координатами (x, y, z) соответствует бесконечное множество однородных координат (x’, y’, z’, a), таких, что x=x’/a, y=y’/a, z=z’/a, то есть однородные координаты определяются с точностью до общего ненулевого множителя. Представляет интерес матрица преобразования, действующая на однородные координаты следующим образом.
или (C)(M) = (P), где (C) – матрица преобразования; (M) – однородные координаты точки пространства M; (P) – соответствующие по отображению координаты в P. В рамках проективной геометрии [26] доказывается теорема о том, что проективное отображение пространства M на пространство P однозначно определяется заданием пяти пар соответствующих по отображению точек, при условии, что из пяти точек, задаваемых в пространстве M, никакие четыре не лежат в одной плоскости. Выбираем пять пар таких опорных точек (M i) и (P i) (верхний индекс соответствует номеру пары) и составляем систему уравнений: (C)(M i)=r i (P i), где i = (1…5), r1, r2, r3 и r4 – неизвестные множители, а r5=1. Решая эти уравнения, находим коэффициенты матрицы проективного преобразования (C), которая в дальнейшем используется для трансформации геометрических примитивов. Описанные проективные преобразования дают возможность реализовать динамическую коррекцию искажений проекционной системы. Данными для вычисления координат опорных точек искривленного объектного пространства являются единичные векторы (хранимые в таблице и пересчитываемые в каждом кадре при динамической коррекции искажений). Орбиты вокруг наблюдателя (на 360 град. во всех направлениях) пересекаются трансформированными пирамидами видимости, которые образуют искаженное сферическое объектное пространство. Для того чтобы не было разрывов поверхностей при больших искажениях, вводится апертура, охватывающая вокселы Д разных уровней пространства. Апертура зависит от степени искажений, при больших искажениях апертуру требуется увеличивать. За счет апертуры и субвоксельного разрешения устраняются дефекты зыбкой границы объектов, так как нет потери отдельных вокселей, а границы хорошо фильтруются. При пересечении воксела последнего уровня с поверхностью мы имеем уравнение касательной плоскости к поверхности в данной точке, а следовательно, и нормали. Интерполяция производится по Фонгу в объектном пространстве с учетом источника освещения и искажений. Текстурируются поверхности с учетом дисторсии; уровни детальности зависят от искажений, которые известны в процессе сканирования пространства, то же самое относится к вычислению функции тумана. Таким образом, комплексно решаются все части данной задачи в отличие от традиционного полигонального задания примитивов, где вначале корректируется форма объектов в процессе разложения многоугольников в телевизионный растр (геометрия ограничивающих многоугольник ребер, при этом многоугольник остается плоским), а затем его цвет, текстура и т.д. с учетом дисторсии. При визуализации поверхностей проверяется тест на принадлежность им лишь пересеченных вокселей, внешние и внутренние вокселы отбраковываются. Если делить и внутреннее пространство, можно выделять объемы. Внутренние вокселы, как и пересеченные, могут быть различных уровней. Для того чтобы повысить реалистичность изображения и расширить класс отображаемых объектов (полупрозрачные структуры с внутренним распределением плотности, 3D текстуры), необходимо отображать внутреннюю полупрозрачную структуру объекта. Для этого в формировании изображения должны участвовать не только вокселы (элементы объема), которые лежат на поверхности, а также и те, которые находятся внутри объекта. Следовательно, при делении объема внутренние части объекта не отбрасываются, для них проводится дальнейшая рекурсия алгоритма. При сканировании объема по X и Y координатам алгоритм работает аналогично алгоритму при рендеринге поверхности: при отсутствии пересечения бруска с объектом данная область пространства отбрасывается, а при их пересечении происходит погружение на следующий уровень рекурсии, пока не достигается максимально возможный уровень, устанавливаемый пользователем. При сканировании сцены по Z координате, что соответствует сканированию объема в глубину, алгоритм не прерывается при встрече с поверхностью, а работает далее, пока полностью не просканируется объем или не накопится определенное значение прозрачности большее некоторого порогового значения. Для уменьшения времени вычислений алгоритм адаптирован к быстрому прохождению однородных областей объектов, для которых совсем необязательно полностью сканировать объем, доходя до последнего уровня рекурсии, а следует проскакивать пустые или однородные участки по Z координате и сразу же вычислять цвет и общую прозрачность. Так как прохождение лучом пустого пространства не вносит вклад в конечное изображение, то скачок через пустое пространство способен обеспечить существенное ускорение обработки, что не влияет на качество изображения. Вследствие того что объемные области могут ограничиваться произвольными поверхностями, можно получить дополнительное ускорение обработки объема. В методе перескока можно эффективно использовать ограничивающие оболочки. Объект, находящийся в объеме, окружается плотно подогнанной произвольной поверхностью – оболочкой, с которой легко вычислить пересечение луча, как уже было описано выше. После нахождения пересечения луча с ограничивающим объектом обход существенной части объема начинается с этой точки пересечения, а не от границы объема. Вычисление цвета Вычисление всех составляющих цвета пиксела производится аналогично по следующим формулам: C=(QambiCambi+QdiffCdiff+QspecCspec)/(Qambi+Qdiff+Qspec); где индекс ambi относится к характеристикам рассеянного излучения, а diff и spec – к диффузной и зеркальной частям отраженного света соответственно; C – компоненты цвета; Q – весовые коэффициенты. Вычисления компонент цвета производятся на основе векторной модели освещения. В расчетах участвуют четыре вектора: нормаль к поверхности (n), вектор на источник освещения (l), направление отраженного света (r) и вектор на наблюдателя (v): Cdiff=(n, l)CliteCsurf , где Clite – цвет источника; Csurf – цвет поверхности. Cspec=(r, v)pClite , где p – коэффициент шероховатости поверхности. При моделировании прохождения света через полупрозрачные среды в целях уменьшения количества вычислений можно не учитывать преломление и затухание вторичных лучей. В случае, когда остается только отражение и затухание света на пути следования от объекта к глазу наблюдателя, формулу, по которой вычисляется цвет пиксела, можно выразить следующим образом [24]:
где Pl – конечный цвет пиксела, а l может быть r, g или b (то есть красный, зеленый или синий соответственно); Iln – интенсивность в n-ом вокселе, вычисленная по модели освещения Фонг; Wn непрозрачность n-го воксела; Il0 отраженный свет от первой точки на луче сканирования; IlN – цвет фона и WN=1. Преодоление порога можно отследить следующим образом: если на k-том шаге общая прозрачность (1–W0)(1–W1)…(1–Wk–1), становится меньше некоторого e, то это значит, что вклад всех следующих за k-тым вокселей будет малым, и поэтому сканирование можно прекратить. Чтобы учесть перспективу, следует внести поправку в алгоритм накопления цвета в пикселе. Дело в том, что размеры воксела в результате трансформации геометрических примитивов становятся зависимыми от координаты Z, поэтому при пересчете цвета в пикселе прозрачность воксела следует также пересчитывать с поправкой на изменение его длины. Проведенные исследования по объемно-ориентированной технологии визуализации позволили выявить ряд преимуществ, как в способе задания сцен, так и в алгоритме растрирования, ориентированных на реализацию в реальном времени. Переход от растрирования в плоскости изображения к растрированию в объеме в сочетании с предлагаемыми способами задания объектов в целом хотя и повышает объем вычислений, выполняемых в реальном времени, но приводит к ряду положительных моментов, повышающих реализм отображаемых сцен. К основным положительным особенностям предлагаемого подхода следует отнести: · эффективность метода растрирования с многоуровневым маскированием, сочетающего простоту вычисления с быстрым поиском и отбраковкой областей, не занятых объектами сцены; · уменьшение количества поверхностей для описания криволинейных объектов (задание объектов поверхностями свободных форм сокращает в 100 и более раз описание баз данных по сравнению с заданием их полигонами); · снижение нагрузки на геометрический процессор и уменьшение потока данных от него в видеопроцессор; · существенное упрощение построения рельефа местности, обусловленное тем, что не требуется предварительная триангуляция поверхностей и клиппирование пирамидой видимости (для смены уровней детальности используется механизм, подобный выборке обычной текстуры [27]); · простое решение задачи динамической коррекции дисторсии за счет предложенного метода проективного преобразования; · возможность обработки воксельных массивов, ограниченных поверхностями свободных форм; · простота анимации и деформации сцен. Перечисленные особенности предлагаемого подхода создают предпосылки к созданию нового класса компьютерных систем визуализации широкого применения. Предварительные оценки показали, что для реализации систем желательна разработка двух заказных СБИС с интеграцией порядка 3 миллионов транзисторов. Первый тип СБИС является конвейером однотипных процессоров, другой тип предназначен для вычисления цвета, тумана, текстуры и фильтрации пикселов. Система будет характеризоваться высоким параллелизмом, однородностью и векторизованностью вычислений. Предлагаемый алгоритм растрирования в сочетании с возможностью визуализации произвольных поверхностей свободных форм и неоднородных объемных областей создают широкий спектр возможных областей применения. Список литературы 1. Pasko A., Adzhiev V., Sourin, A., et al. Function representation in geometric modeling: concepts, implementation and applications //The Visual Computer, 11,6 (429-446), 1995. 2. Savchenko V., Pasko A., Okunev O. and Kunii T., “Function representation of solids reconstructed from scattered surface points and contours”, Computer Graphics Forum, 14,4 (181-188), 1995. 3. Pasko A.A. and Savchenko V.V., “Blending operations for the functionally based constructive geometry”, Set-theoretic Solid Modelling: Techniques and Applications, CSG 94 Conference Proceedings, Information Geometers, Winchester, UK, (151-161), 1994. 4. Sourin A., Pasko A., Savchenko V., "Using real functions with application to hair modelling", Computer & Graphics, 20, 1(11-19), 1996. 5. Savchenko V.V., Pasko A.A., Kunii T.L., Savchenko A.V., "Feature based sculpting of functionally defined 3D geometric objects", Multimedia Modeling. Towards Information Superhighway, T.S. Chua, H.K. Pung and T.L. Kunii (Eds.), World Scientific, Singapore, (341-348), 1995. 6. Pfister H. et al. A real-time volume rendering architecture using an adaptive resampling scheme for parallel and perspective projections //Proc. of 1998 IEEE Symposium on Volume Visualization. Research Triangle Park, North Carolina, 1998. P. 31. 7. Malzbender T. Fourier Volume Rendering // ACM Trans. on Gr. 1993. 12, № 3. 8. Healy D., Weaver B. Adapted wavelet encoding in functional magnetic resonance imaging //Proc. of 1999 SPIE’s 13th Annual International Symposium on Aerospace/Defense Sensing, Simulation, and Controls, Orlando, Florida, 1999. 9. Yagel R., Machiraju R. Data Parallel Volume Rendering Algorithms // The Visual Computer. 1995. 11(6). P. 319. 10.Yagel R. Towards real time volume rendering // GraphiCon'96, St.Petersburg, 1996. P. 230. 11.Savchenko V.V., Pasko A.A. Vyatkin S.I. et al. New approach in geometric modeling: distributed and hardware implementation perspectives.// International Conference on Computers and Devices for Communication CODEC-98. Calcutta, India, 1998. P. 285. 12.Vezina G., Fletcher P., Robertson P. K. Volume Rendering on the MasPar MP-1 // Proc. of 1992 Workshop on Volume Visualization. Boston, MA, 1992. 13.Schroeder P., Salem J.B. Fast Rotation of Volume Data on Data Parallel Architecture // Proc. of Visualization'91, San Diego, 1991. P. 50. 14.Westover L. Footprint Evaluation for Volume Rendering // Computer Graphics 1990. 24(4) P. 37. 15.Fuchs H., Poulton J., Eyles J. et al. Pixel-Planes 5: A heterogeneous multiprocessor graphics system using processor-enhanced memories // Computer Graphics 1989. 23. № 3, P. 79. 16.Fuchs H. Direct visualisation of Volume Data. Volume-based Anatomical Application // IEEE CG & Applications. 1992. 12(4). P. 63. 17.Lacroute P. Real-Time Volume Rendering on Shared Memory Multiprocessors Using the Shear-Warp Factorization // Proc. 1995 Parallel Rendering Symposium, Atlanta, Georgia, 1995. P. 15. 18.Amin A.B., Grama A., Singh V. Fast Volume Rendering Using an Efficient, Scalable Parallel Formulation of the Shear-Warp Algorithm // Proc. 1995 Parallel Rendering Symposium, Atlanta, Georgia, 1995, P. 7. 19.Neih J., Levoy. M. Volume Rendering on Scalable Shared Memory Architecture // Proc. of 1992 Workshop on Volume Visualization, Boston, MA, 1992. P. 17. 20.Montani C., Perego R., Scopingo R. Parallel Volume Visualization on a Hypercube Architecture // Proc. of 1992 Workshop on Volume Visualization, MA, 1992. P. 9. 21.Corrie B., Mackerras P. Parallel Volume Rendering and Data Coherence on the Fujitsu AP1000 // Technical Report TR-CS-92-11, Department of Computer Science, Australian National University, Canberra, ACT, Australia, 1992. 22.Law A., Yagel R. Exploiting Spatial, Ray, and Frame Coherency for Efficient Parallel Volume Rendering // GraphiCon'96, St.Petersburg, 1996. 23.Law A., Yagel R. CellFlow: A Parallel Rendering Scheme for Distributed Memory Architectures // Proc. of International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA'95), 1995, P.1. 24.Knittel G. Voxel Engine for Real-time Visualization and Examination // Eurographics’93. 12. 25.Вяткин С.И., Долговесов Б.С. Чижик С.Е. Синтез виртуальной среды с рекурсивным делением объектного пространства // Графикон ’98.- М., 1998. 26.Ефимов Н.В. Высшая геометрия. - М.: Наука, 1978. - C. 324-338. 27. Vyatkin S.I., Dolgovesov B.S., Ovechkin V.V. et al. Photorealistic imaging of digital terrains, freeforms and thematic textures in realtime visualization system Voxel-Volumes // GraphiCon’97. Moscow. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=944 |
Версия для печати Выпуск в формате PDF (1.07Мб) |
| Статья опубликована в выпуске журнала № 3 за 1999 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Эволюционная модель формирования структур виртуальных предприятий
- Оптимизация обработки информационных запросов в СУБД
- Алгоритмы и программное обеспечение системы обработки топопланов
- О выборе числа процессоров в многопроцессорной вычислительной системе
- Обработка запросов сервером геоинформационной справочной системы
Назад, к списку статей



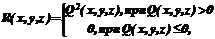 ,
,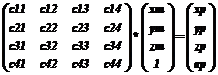
 ,
,