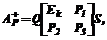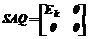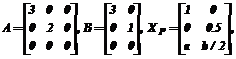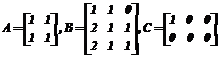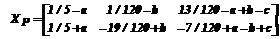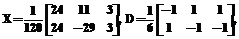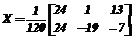Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Параметризованные обобщенные обратные матрицы и решение специальных матричных уравнений
Аннотация:
Abstract:
| Автор: Демидов Н.Е. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 16714 |
Версия для печати Выпуск в формате PDF (1.07Мб) |
Во многих приложениях (линейная алгебра, математическая статистика, теория управления, математическое программирование и др.) используются следующие специальные линейные и нелинейные матричные алгебраические уравнения с заданными матрицами A и B полного или неполного строчного (столбцового) ранга: · AX=XAT, X=XT (матрица X – правый симметризатор матрицы A), · XA=ATX, X=XT (X – левый симметриза- тор A), · AX=B, X=XT (симметричная прокрустова задача), · AX=B, X-1=XT (ортогональная прокрустова задача), · AX=B, XXT=E (несбалансированная ортогональная прокрустова задача; A и B имеют разное число столбцов, E – единичная матрица), · AX+XAT=C (уравнение Ляпунова; C и X – симметричные), · AX+XB=C (уравнение Сильвестра; X – прямоугольная). Решение подобных уравнений сопряжено со сложными вычислительными проблемами [1-3], в связи с чем предлагается унифицированный подход, основанный на использовании параметризованных обобщенных обратных матриц [4]. В настоящее время получили широкое применение различные типы обобщенных обратных (псевдообратных, квазиобратных) матриц (ООМ) [5,6]. Для расчета основных типов ООМ, и в первую очередь ООМ Мура–Пенроуза [5], имеются теоретически обоснованные надежные вычислительные алгоритмы и высокоэффективные программные модули, их реализующие. В специальной литературе проблемы использования ООМ связываются обычно с решением систем линейных алгебраических уравнений (СЛАУ) с прямоугольными матрицами неполного строчного или столбцового ранга. Известное соотношение для получения общего решения матричного уравнения вида AX=B с прямоугольной матрицей A размера n на m (n X=A+B+(Em–A+A)Y связывает исходную матрицу A, ее конкретную ООМ A+ и частное решение X0=A+B со свободными параметрами в виде матрицы Y того же размера, что и X, то есть является сверхпараметризованным (Em – единичная матрица порядка m). В практических задачах возникает проблема использования минимального числа свободных параметров, то есть проблема минимальной параметризации A+ и X, в частности для уменьшения вычислительной сложности алгоритмов. Минимальные и аппроксимирующие параметризации ООМ и решений СЛАУ открывают также и новые возможности решения многих задач оптимизации и управления [4]. Предложенное единое параметризованное представление ряда известных типов ООМ
полученное для исходной матрицы A с помощью преобразования ее к виду
(диагональная редукция [6], S и Q – обратимые матрицы), позволило разработать унифицированную схему вычисления ООМ и решений СЛАУ Xp=Ap+B с минимальным или заданным аппроксимирующим числом свободных параметров [4]. Рассмотрим проблемы нахождения точных или параметризованных МНК–решений перечисленных выше уравнений и возможности предлагаемого подхода с использованием параметризованных ООМ и решений СЛАУ на конкретных примерах, приведенных в [1-3]. Нахождение симметризаторов [1]. Симметризаторы используются при преобразовании задачи на собственные значения для несимметричных матриц в аналогичную задачу для симметричных матриц, которая решается на порядок проще, и в других приложениях, в частности в статистической теории оценивания. Известен ряд сложных алгоритмов нахождения точных симметризаторов, использующих соответственно кронекеровское произведение и специальную матрицу связи, сингулярное разложение, p – адическую арифметику или арифметику остатков по составному модулю. На основе предлагаемого в [1] подхода для примера с матрицей A вида
получено параметризованное решение
дающее при при конкретных значениях свободных параметров a, b и c все приведенные в [1] левые симметризаторы X. Несбалансированная ортогональная прокрустова задача [2]. Подобные задачи возникают в математической статистике (факторный анализ), в теории управления и в других приложениях. Известные алгоритмы решения данной задачи весьма сложны и используют рекурсивно сингулярное разложение произведения двух матриц и поиск глобального экстремума вспомогательной функции, аргументами которой являются значения элементов заданной строки X. С использованием параметризованной ООМ для матрицы A из [2] получено параметризованное представление Xp
а из системы нелинейных уравнений XTX=E найдены значения параметров a=0 и b=Ö3, определяющих точное решение X. Уравнение Сильвестра [3]. Если матрицы A и B – вырожденные, то точного решения данного уравнения не существует (несовместное вырожденное уравнение – inconsistent singular equation), а приближенное решение обычно минимизирует одну из известных матричных норм для разности D=AX+XB–C. Для получения МНК–решения в [3] используется сумма кронекеровских произведений M=E°A+BT°E, вычисляются проекторы M+M и MM+ и осуществляются преобразования матриц к форме Хессенберга, а далее решается ряд вспомогательных СЛАУ и применяется один из известных численных методов решения невырожденного уравнения Сильвестра [7]. Использование параметризованных ООМ для матриц A и B позволило уменьшить вычислительную сложность решаемой задачи и получить качественно новые результаты в виде параметризованного представления решения X. Для примера из [3] с матрицами
параметризованное решение
позволяет получить при значениях свободных параметров a=0 и c=0, b – семейство МНК-решений с l2-нормой D, равной 1/6, причем при b= –1/12 – МНК-решение из [3]
а при нулевых значениях a, b и c – решение с минимальной l2 – нормой X Комплекс программных модулей, решающих перечисленные задачи с использованием параметризованных ООМ, оформлен в виде m–файлов системы для математических расчетов MATLAB. Система MATLAB фирмы Mathworks (США), занимающая ведущие позиции в качестве стандартного программного средства для высшей школы в развитых странах, обладает достаточными базовыми возможностями для выполнения таких типовых при вычислении ООМ операций с матрицами, как определение ранга, ортогональные преобразования, разложение по сингулярным числам и другие [8]. Современные версии системы MATLAB обладают также развитыми возможностями для организации символьных вычислений, что позволяет значительно упростить операции с параметризованными матрицами путем использования профессионального инструментального приложения – тулбокса (toolbox) Symbolic Math, включающего пакет линейно-алгебраических операций. Список литературы 1. Sen S. K., Venkaiah V. Ch. On symmetrizing a matrix // Indian J. Pure Appl. Math. – 1988. - 19, №6. – P. 554 – 561. 2. Park H. A parallel algorithm for the unbalanced orthogonal Procrustes problem // Parallel computing. – 1991. – 17, №8. – P. 913 – 923. 3. Lovass-Nagy V., Powers D. L. On least squares solutions of an inconsistent singular equation AX+XB=C // SIAM J. Appl. Math. – 1976, v. 31. - №1. – P. 84 – 88. 4. Демидов Н. Е. Параметризация обобщенных обрат- ных матриц: алгоритмическое и программное обеспече- ние // Программные продукты и системы. - 1998. - №2. - С. 33 – 36. 5. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. - М.: Наука, 1997. -224 с. 6. Грегори Р., Кришнамурти Е. Безошибочные вычисления. Методы и приложения. – М.: Мир, 1988. – 208 с. 7. Икрамов Х. Д. Численное решение матричных уравнений. – М.: Наука, 1984. – 192 с. 8. Потемкин В. Г. Система MATLAB: Справочное пособие. – М.: ДИАЛОГ-МИФИ, 1998. – 350 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=951 |
Версия для печати Выпуск в формате PDF (1.07Мб) |
| Статья опубликована в выпуске журнала № 3 за 1999 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Формирование программ развития больших систем административно-организационного управления
- Формулировка задачи планирования линейных и циклических участков кода
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
Назад, к списку статей