Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимизация общего периода выполнения приложения во встроенных системах реального времени
Аннотация:
Abstract:
| Автор: Перевозчиков М.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 7738 |
Версия для печати Выпуск в формате PDF (2.03Мб) |
Для встроенных программных систем реального времени, построенных в соответствии с хронометрическим подходом, одной из важнейших системных структур данных является график активации задач. Строится он на основе информации о временных ограничениях для каждой задачи, к которым в простейшем случае относится период выполнения задачи, наихудший случай времени выполнения задачи (ТЗ) и относительный срок выполнения. Поскольку все задачи приложения периодические, то существует общий период выполнения приложения (ТП), который равен наименьшему общему кратному (НОК) периодов всех задач. Размер статического графика пропорционален величине ТП. В связи с этим возникает проблема ограничения на размер графика, поскольку для произвольного набора задач (их периодов) он может превысить физические ресурсы аппаратных средств. Уменьшить размер статического графика можно за счет использования информации о значении допусков на периоды активации задач. Введение даже небольших допусков (около 5 %) часто позволяет на порядок уменьшить величину ТП. Однако возникает проблема отыскания оптимального значения ТП и соответствующего ему значения периодов для набора задач с произвольными временными характеристиками. Формальная модель. Для решения этой проблемы формализуем проблемную область, введя специальные обозначения: T – множество задач; ti – i-я задача из множества T; pnom,i – номинальный период i-й задачи; ci – ТЗ i-й задачи;
pact,i – актуальный период i-й задачи, удовлетворяющий следующему условию:
Необходимо найти значение ТП, удовлетворяющее следующим двум условиям. 1. Для каждой задачи ti существует по крайней мере одно значение pact,i, которое целое число раз укладывается в величину ТП:
2. Значение ТП минимальное. Оптимальное в простом смысле значе- ние ТП. Значение ТП, удовлетворяющее приведенным выше двум значениям, назовем оптимальным в простом смысле.
Из рисунка видно, что все значения ТП, большие 18, удовлетворяют ограничениям данной задачи. В общем случае, если допуск отличен от нуля, множество Ei состоит из конечного числа подмножеств. Обозначим j-е подмножество множества Ei как ei, j. Число этих подмножеств назовем размерностью множества Ei и обозначим как hi. Значение размерности можно легко отыскать из следующего предположения:
После несложных преобразований получаем:
Из полученного соотношения видно, что размерность Ei не зависит от значения периода, а зависит только от величины его допусков. Зная размерность, можно определить само множество Ei:
где ei, j = Множество значений ТП G, удовлетворяющих условиям всех задач, можно найти как пересечение всех Ei:
Тогда оптимальное в простом смысле значение ТП равно минимальному числу из G. Для множества из трех задач это проиллюстрировано на рисунке 2 (p1 = 7 ± 1, p2 = 5 ± 1, p3 = 9 ± 1.5). Вычисления оптимального в простом смысле значения ТП. Задача состоит в том, чтобы найти множество G. Прямым решением являются три вложенных цикла, в которых для каждого подмножества множества Ei каждой задачи ищется пересечение со всеми подмножествами Ej других задач. Сложность такого метода составляет O(h2×|T|), где h – средняя размерность множества Ei. Время вычисления значения ТП таким методом катастрофически возрастает при значениях допуска меньших 1 %. Кроме этого, метод не работает, если во множестве T есть задачи с нулевым допуском (поскольку для них множество Ei бесконечно мерно). Поэтому необходим быстрый алгоритм отыскания оптимального значения ТП. Ниже приведен алгоритм, основывающийся на том, что нет необходимости вычислять все множество G, а достаточно найти лишь первое его подмножество. Каждой задаче в этом алгоритме ставится в соответствие структура данных task_info, состоящая из пяти полей: 1. min_period – минимальное значение периода задачи; 2. max_period – максимальное значение периода задачи; 3. left_bound – левая граница текущего подмножества множества Ei; 4. right_bound – правая граница текущего подмножества множества Ei; 5. dimension – размерность множества Ei. Для удобства объединим эти структуры в массив Tasks, размер которого равен числу задач. Перед началом работы алгоритма массив Tasks инициализируется исходя из информации о номинальном периоде задачи и его допусках: Tasks[i].min_period = Tasks[i].max_period = Tasks[i].left_boun = Tasks[i].min_period; (4) Tasks[i].right_boud = Tasks[i].max_period; Tasks[i].dimension = hi (по формуле 2). Результатом алгоритма являются два числа: left_esop_bound и right_esop_bound – левая и правая границы первого подмножества множества G. Искомым оптимальным значением ТП является left_esop_bound. Рассмотрим сам алгоритм: 1. Цикл по i от 2 до |T|: 1.1. Цикл по j от 1 до |T|: 1.1.1. Если Tasks[j].right_bound меньше Tasks[i].left_bound, то сделать текущим подмножеством множества Ej для Tasks[j] подмножество с номером n = 1.1.2. Если Tasks[i].right_bound меньше Tasks[j].left_bound, то сделать текущим подмножеством множества Ei для Tasks[i] подмножество с номером n = 2. Присвоить переменной left_esop_bound значение Tasks[1].left_bound, а переменной right_esop_bound значение Tasks[1].right_bound. 3. Цикл по i от 2 до |T|: 3.1. Если left_esop_bound меньше Tasks[i].left_bound, то присвоить переменной left_esop_bound значение Tasks[i].left_bound: 3.2. Если right_esop_bound больше Tasks[i].right_bound, то присвоить переменной right_esop_bound значение Tasks[i].right_bound. Сложность этого алгоритма не зависит от значений допусков на периоды и составляет O(|T|2) операций, что является приемлемым, поскольку обычно число задач в приложении не превы- шает 100.
Представляется целесообразным выбирать максимальное значение периода (для уменьшения загрузки процессора). Тогда pact,i можно вычислить следующим образом: Pact,i = Для примера из рисунка 2: pact,1 = 8, pact,2 = 4, pact,3 = 8. Оптимальное в полном смысле значение ТП. Описанный алгоритм не учитывает наихудший случай времени выполнения задач. Это может привести к тому, что при вычислении оптимального значения ТП общая загрузка процессора задачами (Uact) превысит максимально допустимую (Umax), хотя для номинального значения периодов этого не происходит, то есть:
Поэтому, исходный набор ограничений необходимо расширить. 1. 2. Значение ТП минимальное. 3. Uact £ Umax. Значение ТП, удовлетворяющее этим трем условиям, назовем оптимальным в полном смысле. Для того чтобы понять как его найти, рассмотрим поведение величины pact,i некоторой задачи в зависимости от величины ТП. В общем случае эта зависимость представляет собой кусочно-линейную функцию, определенную на множестве Ei и изменяющуюся в диапазоне Для множества задач T область определения функции pact,i(ТП) для каждой задачи ограничивается величиной множества G. Необходимым и достаточным условием существования оптимального в полном смысле значения ТП является выполнение соотношения:
Вычисление оптимального в полном смысле значения ТП. Ниже приведен алгоритм последовательного приближения для отыскания такого значения ТП. Он основывается на предыдущем алгоритме и том положении, что если некоторому текущему значению ТП ТП,cur соответствует некоторое значение загрузки процессора Uact, большее Umax, то искомое значение ТП, по крайней мере, не меньше величины ТП,new, определяемой следующим образом:
Если числа ТП,cur и ТП,new находятся на одном интервале линейности функции для каждой задачи из T, то эта величина и есть искомое оптимальное значение. В противном случае оптимальное значение превышает ТП,new. При этом предполагается, что нет оптимального значения ТП, меньшего ТП,cur. Теперь вернемся к первому алгоритму. В общем случае то, какое именно подмножество множества G отыскивает этот алгоритм, зависит от начальных условий (значений элементов массива Tasks). Кроме этого, если алгоритм нашел некоторое i-е подмножество множества G, то начальные условия для отыскания (i+1)-го подмножества формируются из полученного массива Tasks следующим образом. 1. Ищется элемент массива Tasks с минимальным значением поля right_bound. 2. Для задачи, соответствующей найденному элементу, делается текущим следующее по порядку подмножества множества Ei (если номер текущего подмножества – n, то left_bound и right_bound инициализируются значениями, соответствующими ei,n+1). Модифицированный таким образом массив Tasks представляет начальные условия для поиска следующего по порядку подмножества множества G. Для упрощения выполнения второй операции можно в структуру task_info добавить шестое поле count, в котором для каждой задачи будет храниться номер текущего подмножества множества Ei. Ниже приведен сам алгоритм отыскания оптимального в полном смысле значения ТП. 1. Проверить условие (7). Если оно не выполняется, завершить алгоритм с отрицательным результатом. 2. Проинициализировать массив Tasks согласно (4). 3. Найти соответствующее данному состоянию массива Tasks подмножество множества G (используя предыдущий алгоритм). 4. Присвоить переменной ТП,cur значение left_esop_bound. 5. Для всех задач вычислить актуальное значение периода pact,i, соответствующее ТП,cur, согласно (5). 6. Вычислить актуальное значение загрузки процессора Uact согласно (6). 7. Если Uact £ Umax, то завершить алгоритм с положительным результатом (искомым значением ТП является ТП,cur). 8. Вычислить значение ТП,new согласно (8). 9. Если ТП,new £ right_esop_bound, то присвоить переменной ТП,cur значение ТП,new и вернуться к шагу 5. 10. Найти i-й элемент массива Tasks с минимальным значением поля right_bound. 11. Проинициализировать Tasks[i].left_bound и Tasks[i].right_bound значениями, соответствующими ei,(Tasks[i].count+1) согласно (3). 12. Найти соответствующее данному состоянию массива Tasks подмножество множества G (используя предыдущий алгоритм). 13. Если ТП,new > right_esop_bound, то вернуться к шагу 10. 14. Присвоить переменной ТП,cur значение max(left_esop_bound, ESOPnew). 15. Вернуться к шагу 5. Одной из важнейших системных структур данных для хронометрических систем реального времени является график активации задач. Размер его пропорционален ТП, который в простейшем случае вычисляется как наименьше общее кратное периодов задач приложения. В общем случае его размер может превышать доступные физические ресурсы. Одним из способов сокращения размера графика является его оптимизация на основе информации о величине допуска на период выполнения задачи. Для примера встроенного приложения реального времени** введение допуска всего в 1 % позволило почти в 200 раз уменьшить величину ТП. В данной работе описаны два алгоритма отыскания оптимального значения ТП. Первый алгоритм не учитывает информацию о наихудшем случае времени выполнения задачи, поэтому его можно использовать только в тех случаях, когда заведомо известно, что загрузка процессора будет невелика. Второй алгоритм более трудоемок, но применим во всех случаях, поскольку находит оптимальное значение ТП, учитывая величину загрузки процессора. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=960 |
Версия для печати Выпуск в формате PDF (2.03Мб) |
| Статья опубликована в выпуске журнала № 4 за 1999 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
- Компьютер - хранитель домашнего очага
- Автоматизированная система принятия решений при стратегическом планировании устойчивого развития региона в условиях нечеткой информации
- Компьютерный тренажер для операторов технологических процессов доменного производства
- Общедоступные математические САПР для персональных компьютеров класса IBM PC
Назад, к списку статей



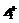 – допуск в большую сторону на период i-й задачи;
– допуск в большую сторону на период i-й задачи; – допуск в меньшую сторону на период i-й задачи.
– допуск в меньшую сторону на период i-й задачи.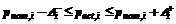 .
. ; (1)
; (1)![Подпись: G = {8} È [15, 16] È [18, 21] È [22.5, ¥); ТП = 8; НОК(5, 7, 9) = 315.Рис. 2. Отыскание оптимального в простом смысле значения ТП](uploaded/image/1999-4/image282.gif)
 Для каждой задачи ti можно построить множество Ei всех возможных значений ТП, удовлетворяющих первому условию. На рисунке 1 изображено такое множество для задачи с периодом, равным 7 и допуском ±1.
Для каждой задачи ti можно построить множество Ei всех возможных значений ТП, удовлетворяющих первому условию. На рисунке 1 изображено такое множество для задачи с периодом, равным 7 и допуском ±1. .
.
 где k=
где k= . (2)
. (2)
 . (3)
. (3)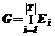 .
. ;
; ;
;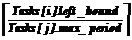 *.
*. и начать цикл с шага 1.1 заново.
и начать цикл с шага 1.1 заново.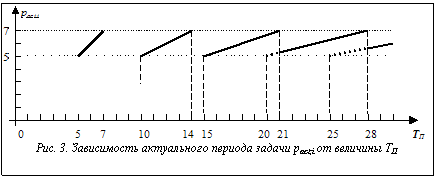 Вычисление значений периодов активации задач. Исходя из полученного значения ТП, необходимо для всех задач определить pact,i. Для каждой задачи может существовать несколько значений pact,i, которые определяются по формуле 1 исходя из значения ni, находящегося в следующем диапазоне:
Вычисление значений периодов активации задач. Исходя из полученного значения ТП, необходимо для всех задач определить pact,i. Для каждой задачи может существовать несколько значений pact,i, которые определяются по формуле 1 исходя из значения ni, находящегося в следующем диапазоне: .
. . (5)
. (5)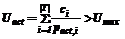 . (6)
. (6) .
. . Для задачи с номинальным периодом, равным 6 и допуском ±1, эта зависимость приведена на ри- сунке 3.
. Для задачи с номинальным периодом, равным 6 и допуском ±1, эта зависимость приведена на ри- сунке 3. . (7)
. (7) . (8)
. (8)