Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Статистический анализ структуры пользовательского интерфейса
Аннотация:
Abstract:
| Авторы: Мустафин Н.Г. () - , Савосин С.В. () - , Музяков И.Р. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 8749 |
Версия для печати Выпуск в формате PDF (2.03Мб) |
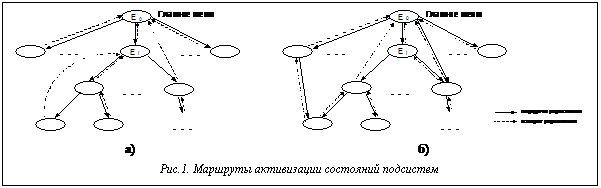
В настоящее время существуют мощные инструментальные средства, значительно упрощающие программирование приложений. Одной из проблем, возникающих при создании программного продукта, является разработка продуманной структуры взаимодействия программных модулей, которая включает в себя, в частности, проектирование пользовательского интерфейса. Часто быстрое проектирование и визуальное программирование приводит к перегруженности и непродуманности структуры пользовательского интерфейса и структуры вызовов программных модулей. Этому факту есть объяснение: на этапе проектирования программного продукта бывает достаточно сложно разработать эффективную структуру функционирования системы (СФС). Будем рассматривать частную задачу автоматизации модификации системы, которая заключается в выявления узких мест в функциональной структуре системы. Предлагается для анализа и модификации СФС использовать статистику временного распределения функционирования системы, полученную в процессе ее эксплуатации. Данные по фактической активизации функциональных элементов (ФЭ) представляются в виде графа, который будем называть графом фактических состояний системы (ГФС). Возникает необходимость анализа ГФС и выявление предпочтений в пользовательских маршрутах активизации ФЭ (для маршрутов не менее заданного порядка). Эта информация рассчитывается на базе значений матрицы переходных вероятностей ГФС. Значения переходных вероятностей смены состояний с заданной достоверностью могут быть получены как результат обработки фактической статистической информации о функционировании системы. Фактическая статистическая информация накапливается при регистрации событий смены рабочих состояний в процессе эксплуатации системы. В качестве статистической информации используются данные, характеризующие каждое регистрируемое событие. К ним относится идентификатор фокусируемого ФЭ и абсолютное время перехода в состояние (дата, время). Для вспомогательных целей необходимо дополнительно отмечать события начала работы с подзадачей (активизация главного меню) и события выхода из подсистемы (планового из главного меню или аварийного из произвольного состояния). Обработка полученных статистических данных должна ориентироваться на моделирование процесса функционирования системы как стохастического процесса. При построении и анализе ГФС используются следующие утверждения: · активизация (вызов) ФЭ имеет стохастическую природу; · в качестве объекта анализа рассматривается отдельная подзадача системы; · нахождение системы в состоянии Еj стохастического процесса сопоставляется с состоянием активизации (вызова) ФЭ; · начальное состояние Е0 соответствует нахождению системы в состоянии главного ме- ню подзадачи, при этом вероятности нахождения в начальном состоянии: p(0)1 = 1; p(0)j = 0 для j=2,3,…; · считается, что переходные вероятности стационарны во времени, так как определяются непосредственно функциональными свойствами подсистемы и неизменными функциональными требованиями к подсистеме (на анализируемом временном участке жизненного цикла системы); · в самом простом случае вероятность наступления текущего состояния зависит только от непосредственно предшествующего состояния. Последнее утверждение выполняется лишь в том случае, если рассматривать модель функционирования системы с тем допущением, что любое состояние системы из корневого состояния может быть достигнуто одним путем при рассмотрении только прямых маршрутов (без возвратов). Тогда каждое состояние может быть активизировано (под активизацией понимается включение ФЭ в фокусное дерево) только из одного определенного активизирующего состояния (рис. 1,а). Утверждение нарушается, если существуют состояния, которые могут быть достигнуты более чем одним прямым маршрутом. При существующих программных механизмах перехода системы по фокусному дереву возврат к корневому состоянию происходит (при наличии альтернативы и отсутствии непосредственного управления) по пути, который соответствует обратному порядку активизации (рис.1,б). Аналогично при возврате из вычислительного процесса (при отсутствии непосредственного управления переходом) система возвращается в состояние, из которого произошел вызов процесса. Данная стохастическая система напоминает сложную цепь Маркова 2-го порядка, когда вероятность нового состояния зависит от 2-х состояний системы, непосредственно ему предшествующих [1]. Однако в рассматриваемом случае ситуация несколько отлична: переходная вероятность наступления текущего состояния зависит от непосредственно предшествующего состояния, а также оттого, из какого состояния было активизировано это предшествующее состояние. Переходная вероятность такого стохастического процесса может быть представлена в следующем виде:
где pijk – одношаговая вероятность перехода из состояния i в момент времени tn-1 в состояние j в момент tn при условии, что состояние i было активизировано из состояния k в момент времени tAct(n-1) при tAct(n-1) < tn-1 и k ¹ i. Следовательно, рассматриваемая система обладает ограниченным последействием. Матрица переходных вероятностей приобретает вид:
где переходные вероятности из состояния i в состояние j задаются вектором:
Таким образом, при обработке статистических данных при построении матрицы переходных вероятностей системы P[i,j,k] требуется отслеживать историю смены состояний при проходе по ГФС в прямом направлении. Рассмотрим в общем виде схемы некоторых из возможных вариантов анализа системы с использованием значений одношаговых переходных вероятностей. Выбираются граничные значения: nш – порядок маршрутов (количество шагов – смен состояний), pгр – граничное значение переходной вероятности, при превышении которого вероятность наступления события будем считать большой, событие перехода по данному маршруту порядка не меньше nш будем называть типовым, а сам маршрут – типовым пользовательским маршрутом. Граничные значения выбираются экспериментальным путем, можно предложить следующие эмпирические соотношения:
где Nперех – количество ненулевых значений pijk. Для анализа ГФС и поиска типовых маршрутов могут быть использованы различные алго- ритмы. Самый простой, но и самый трудоемкий ме- тод – это полный перебор всех маршрутов порядка не менее nш: nш, nш+1, nш+2,… (в случае полного перебора необходимо дополнительно задать и верхний предел порядка маршрута). Для каждого маршрута анализируется вероятность перехода из состояния начала маршрута до завершающего маршрут состояния (через промежуточные состояния данного маршрута!). Обозначим такую вероятность как pijм , где м={ i, k1 ,…, ks , j} – последовательный список состояний маршрута, k1 ,…, ks – промежуточные состояния маршрута.
Метод полного перебора можно улучшить с использованием варианта метода ветвей и границ [3]. В качестве условия отсечки ветвей просмотра используется тот факт, что если в маршрут i ® j входит переход первого порядка из состояния Ea в состояние Еb с переходной вероятностью pab < pгр , то pij < pгр , то есть маршрут не будет являться предпочтительным, и поиск по этой ветви графа прекращается. Статистика фактического временного распределения нахождения системы в рабочих состояниях (активизация, вызов ФЭ) позволяет оценить вероятности абсолютного временного распределения состояний системы.
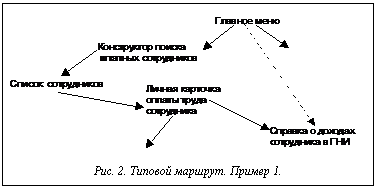
где N – количество состояний; wi – относительное время нахождения подсистемы в i-м состоянии (определяется на основе обработки статистических данных о функционировании системы). Выявленные типовые (а тем более критические типовые) маршруты анализируются, и (если имеется возможность) в систему вводятся дополнительные более короткие маршруты. В идеале следует стремиться к появлению в ГФС дополнительно к маршруту i®k1®…®ks®j маршру- та i®j. В качестве пояснения рассмотрим некоторые примеры. Анализируем маршруты в подсистеме «Учет и расчет заработной платы» ИУС «Бухгалтерский учет». Выявлен типовой маршрут Главное меню ® …®Справка о доходах сотрудника в ГНИ, схема которого показана на рисунке 2. Система может быть модифицирована добавлением непосредственного вызова состояния Справка о доходах сотрудника в ГНИ из состояния Главное меню (пунктирная линия на рисунке). Такая модификация возможна, так как обычно возникает ситуация получения данной справки для сотрудника с заранее известным уникальным идентификатором – табельным номером, и, следовательно, использование дополнительных поисковых операций не является обязательным. Может возникать и другая ситуация. Выявлен типовой маршрут Список сотрудников®…®Главное меню ® Табель учета рабочего времени. Отличие от предыдущего примера в том, что типовой маршрут составляют не только прямые переходы (от главного меню), но и обратные (возврат к главному меню). Система может быть модифицирована добавлением непосредственного вызова состояния Табель учета рабочего времени из состояния Список сотрудника (пунктирная линия на рисунке 3). Таким образом, модификации рассмотренного типа позволяют разгрузить типовые критические маршруты, тем самым предоставляя пользователю более удобный интерфейс, уменьшая время выполнения операций, связанных с навигацией в рамках пользовательского интерфейса. Список литературы 1. Тихонов В.И., Миронов М.А. Марковские процессы. - М.: Сов. радио, 1977. - 488 с. 2. Карлин С. Основы теории случайных процессов. /Пер. с англ. - М.: Мир, 1971. - 536 с. 3. Романовский И.В. Алгоритмы решения экстремальных задач. - М.: Наука, 1977. - 352 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=966 |
Версия для печати Выпуск в формате PDF (2.03Мб) |
| Статья опубликована в выпуске журнала № 4 за 1999 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Эволюционная модель формирования структур виртуальных предприятий
- О выборе числа процессоров в многопроцессорной вычислительной системе
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Вычислительный интеллект: немонотонные логики и графическое представление знаний
- К вопросу параметризации свойств программных средств обучения
Назад, к списку статей



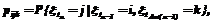
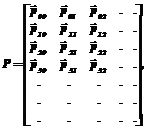
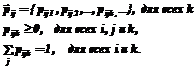
 Рассматриваемая сложная цепь Маркова может быть сведена к простой цепи Маркова для случайного двухмерного вектора
Рассматриваемая сложная цепь Маркова может быть сведена к простой цепи Маркова для случайного двухмерного вектора 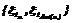 , и ГФС описывает переходный режим на произвольных интервалах времени в виде сложной цепи Маркова (при возвращении по цепи учитывается прямой путь). При описании в виде Марковского процесса ГФС может быть проанализирован с использованием математического аппарата, применяемого для Марковских цепей [1,2].
, и ГФС описывает переходный режим на произвольных интервалах времени в виде сложной цепи Маркова (при возвращении по цепи учитывается прямой путь). При описании в виде Марковского процесса ГФС может быть проанализирован с использованием математического аппарата, применяемого для Марковских цепей [1,2].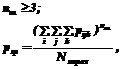
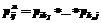 .
. Информация о временном распределении нахождения системы в рабочих состояниях для типовых пользовательских маршрутов позволяет выделить критические пользовательские маршруты. Критическим будем называть типовой маршрут, включающий одно или несколько состояний, относительное время использования которых достаточно велико, то есть превышает некоторое эмпирическое граничное значение, например:
Информация о временном распределении нахождения системы в рабочих состояниях для типовых пользовательских маршрутов позволяет выделить критические пользовательские маршруты. Критическим будем называть типовой маршрут, включающий одно или несколько состояний, относительное время использования которых достаточно велико, то есть превышает некоторое эмпирическое граничное значение, например: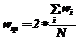 ,
,