Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритмизация задач нелинейной динамики в процессах массовой кристаллизации из растворов
Аннотация:
Abstract:
| Авторы: Гордеев Л.С. (l.s.gordeev@yandex.ru) - Российский химико-технологический университет им. Д.И. Менделеева, Москва, Россия, доктор технических наук, Кольцова Э.М. (kolts@muctr.ru) - Российский химико-технологический университет им. Д.И. Менделеева (профессор), Москва, Россия, доктор технических наук, Аганина А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 12069 |
Версия для печати Выпуск в формате PDF (1.60Мб) |
Вычислительный эксперимент дает возможность анализировать нелинейные явления в химии, физике, биологии, социологии, приводит к рождению новых идей, теорий, методов, к развитию междисциплинарных подходов, помогает сформулировать новые понятия и открыть замечательные явления природы. Наиболее удивительное в области моделирования состоит в том, что небольшое число сравнительно простых математических моделей дает ключ к пониманию и исследованию огромного количества различных нелинейных явлений. Объектом нелинейной динамики являются процессы массовой кристаллизации из растворов малорастворимых веществ. Рассмотрим процесс кристаллизации малорастворимого вещества – двухосновного фосфита свинца, получаемого в ходе химической реакции Na2HPO3+2PbO*Pb(CH3COO)2*0.5H2O= =2PbO*PbHPO3*0.5H2O¯+2NaCH3COO. Процесс кристаллизации моделировали таким образом, чтобы было возможным отследить колебательные режимы скорости роста кристаллов малорастворимого вещества. В основе математической модели лежат представления о кластерах – это устойчивые образования, которые формируются в пересыщенном растворе в ходе серии бимолекулярных реакций между ионами или молекулами растворенного вещества. Кластеры, достигшие критического размера, расходуются на образование зародышей и играют важную роль в росте кристалла: кластеры диффундируют к поверхности растущего кристалла и ожидают в некоторой очереди кластеров со случайной ориентацией на поверхности, что приводит к значительной пленке кластеров, нуждающейся во встраивании в кристаллическую решетку [1]. По такому механизму рост кристаллов как бы квантуется порциями этих кластеров. Причем раствор то обедняется ими за счет роста и образования зародышей, то обогащается ими за счет создания пересыщения путем химической реакции. Моделирование процессов кристаллизации малорастворимых веществ (на примере кристаллизации двухосновного фосфита свинца 2PbO*PbHPO3*0.5H2O) Математическая модель процесса кристаллизации двухосновного фосфита свинца имеет следующий вид (экспериментальные исследования проводились при фиксированной температуре T=const=20 оС). Уравнения изменения концентраций реагентов:
Уравнение изменения концентрации фосфита свинца за счет химической реакции:
Уравнение изменения числа кластеров:
Уравнение баланса числа кристаллов:
Граничное условие:
Начальные условия: t=0, с1(0)=с10, с2(0)=с20, с3(0)=0, с4(0)=0, n(0)=0, N(0,k)=0, h(0,k)=0, где сi – концентрация i-го реагента; g1,g2,g3 – коэффициенты соотношения масс компонентов; vq – скорость прилива фосфита натрия; V – объем раствора; r0 – плотность кристаллов фосфита свинца; r0 – объем кластера; cS – равновесная концентрация фосфита свинца; k1 – константа скорости химической реакции; k0 – константа скорости образования кластеров; n – число кластеров в растворе; b1 – константа скорости зародышеобразования; b2 – константа скорости роста кристалла; b3 – константа степени зависимости скорости роста кристалла h от числа кластеров в растущем кристалле; h(k) – скорость роста кристалла; k – количество кластеров в растущем кристалле; t – время; N(k)dk – число кристаллов, содержащих количество кластеров от k до k+dk; В уравнении изменения числа кластеров первое слагаемое в правой части характеризует приход кластеров за счет их образования при создании пересыщения в растворе, второе и третье слагаемые характеризуют уход кластеров за счет возникновения зародышей и роста кристаллов соответственно. В уравнении баланса числа кристаллов скорость роста кристалла является функцией количества свободных кластеров в растворе. Алгоритм решения системы (1) основан на использовании явной разностной схемы с n разбиением по времени. Система уравнений математической модели (1) записывается в виде дискретных уравнений с шагом квантования по времени, равным времени образования устойчивого кластера 2-6 с.
Методом случайного поиска, используя функцию рассогласования, включающую экспериментальные и рассчитанные по модели значения массы осадка, концентраций основных реагентов и среднего размера образующихся кристаллов, были найдены кинетические константы модели: k1 = 1.67*10-3 м3/кг*сек, k0 = 1.66*1016 1/ м3*сек, b1 = 7*10-23 сек/ м3 , b2 = 1.25*10-20 м3/ сек , b3 = 2/3. В качестве линейного размера кластера на основании работ [2-5] был принят размер 4 нм. Расчетным путем было получено, что состоянию насыщения раствора соответствует число кластеров nS = 1*10-1 1/м3. Уравнение изменения концентрации кристаллизующегося продукта и уравнение изменения числа кластеров, записанные в виде дискретных уравнений системы
(Dt – шаг квантования по времени), линейными преобразованиями приводятся к уравнениям, близким по типу к логистическому уравнению
хорошо исследованному М. Фейгенбаумом [6]. Причем l параметр логистического уравнения (3) является переменным. Для периодического ( – для уравнения изменения концентрации фосфита свинца за счет химической реакции:
– для уравнения изменения числа кластеров:
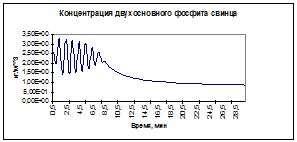
Рис. 1
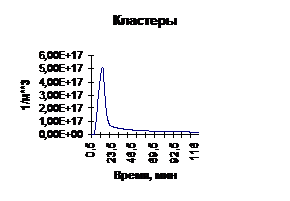
Рис. 2 Уравнения (4) и (5) представляют собой систему двух взаимосвязанных осцилляторов, которые в зависимости от скорости подачи реагента могут описывать колебания концентрации двухосновного фосфита свинца, числа кластеров и скорости роста кристаллов (как функции, зависящей от числа кластеров в растворе). Бифуркационным параметром системы (2) является скорость прилива реагента. Бифуркационным значением этого параметра является vq =0.01 мл/сек. Качественное поведение кинетических кривых для скоростей прилива реагента, меньших бифуркационного значения, представлено на рисунках 1 и 2. Концентрация двухосновного фосфита свинца уже за первые пять минут достигает максимального значения, которое остается неизменным вплоть до окончания реакции. Число кластеров на 5–10 минуте достигает максимального значения, а затем резко уменьшается и асимптотически приближается к значению числа кластеров в насыщенном растворе. Качественная картина плотности функции распределения по количеству кластеров представлена на рисунке 3. Эволюция функции распределения характеризуется смещением максимума в сторону увеличения количества кластеров (размера кристалла). При малых скоростях прилива реагента образуется малое количество кристаллов с наиболее вероятным размером 300-800 кластеров. Параметр l как для концентрации кристаллизующегося вещества, так и для числа кластеров (lc и ln) медленно увеличивается за время процесса, не превышая величины lc=2 и ln=2, что соответствует выходу кривых на равновесное состояние, характерное для насыщенного раствора. При увеличении скорости подачи реагента vq>0.01 мл/сек наблюдается возникновение колебаний концентрации кристаллизующегося вещества и числа кластеров в растворе. Причиной возникновения осцилляций концентрации является конкурентная борьба между источником пересыщения в ходе химической реакции и стоком пересыщения за счет образования кластеров. Параметр логистического уравнения (4) lc состоит как из элементов скорости химической реакции, так и из элементов скорости образования кластеров. Причиной возникновения осцилляций числа кластеров в растворе является борьба между источником образования кластеров и уходом кластеров в зародыши и рост кристаллов. Параметр логистического уравнения (5) ln состоит из элемента, отражающего уход в образование зародышей и рост кристаллов, и из элементов, характеризующих образование кластеров в ходе химической реакции.
Рис. 3
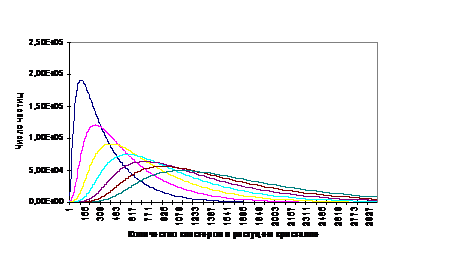
Рис. 4 Качественная характеристика кинетической кривой числа кластеров для больших скоростей прилива показана на рисунке 4. Число кластеров увеличивается в течение первых пяти минут, что соответствует значению ln =3.24, затем наблюдаются хаотические колебания, параметр ln при этом изменяется от 3.24 до 4. При увеличении ln > 4 (ln может увеличиваться до 40) квадратичное отображение трансформируется в отображение с вынужденным управлением. Как только потребность растущего кристалла в кластерах превышает их резервы, накопленные в ходе реакции (параметр ln > 4), число кластеров принимает значение, равное числу кластеров в насыщенном растворе, до тех пор пока не накопится вновь некоторая критическая масса кластеров за счет химической реакции. При разных скоростях прилива реагента кривая зависимости числа кластеров от времени проходит через максимум на первой стадии кристаллизации, что свидетельствует о более высоком содержании кластеров в начальном периоде кристаллизации, пока не появилось достаточное число зародышей и кристаллов двухосновного фосфита свинца. На рисунке 5 видно, что в первые две минуты наблюдается увеличение концентрации кристаллизующегося вещества, что соответствует увеличению значения параметра уравнения (5) lc до 3.24; при значениях 3.243.56, затем при уменьшении lc от 3.6 до 1.5 наблюдается переход от хаоса к порядку и выход на стационарный режим, концентрация асимптотически приближается к концентрации насыщенного раствора.
Рис. 5 Для скоростей прилива реагента, больших бифуркационной, эволюция функции распределения с течением времени может быть двух видов – бимодальная, так как за счет увеличения скорости прилива реагента наблюдается значительное образование мельчайших кристаллов на ряду с кристаллами с уже развитой кристаллической поверхностью, и одномодальная с наиболее вероятным размером кристаллов 50-100 кластеров. Рассмотрим процесс кристаллизации двухосновного фосфита свинца в непрерывном режиме (
При значениях параметра логистического уравнения 0
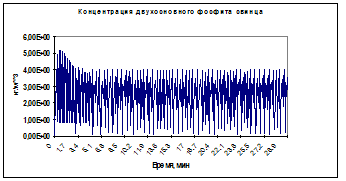
Рис. 6 Исследовали поведение концентрации двухосновного фосфита свинца и числа кластеров в зависимости от изменения скорости прилива реагента (от 0.005 до 4.2 мл/сек). Можно выделить несколько различных качественных картин изменения концентрации двухосновного фосфита свинца: в диапазоне скоростей 0.5–1.5 мл/сек наблюдается выход концентрации на стационарное состояние; 2–3 мл/сек – колебания с удвоением периода; 3.2– 3.5 мл/сек – колебания с учетверением периода и так далее с периодом соответственно 8Dt, 16Dt, 32Dt, 64Dt. Когда скорость прилива реагента достигает 3.7 мл/сек (и в диапазоне скоростей 3.7– 4.05 мл/сек), наблюдаются хаотические колебания концентрации двухосновного фосфита свинца, как показано на рисун-ке 6. Управление хаосом Естественно, при наблюдении подобных явлений при кристаллизации возникают вопросы: что является причиной колебаний при кристаллизации, образование каких веществ носит ритмический характер. С помощью методов неравновесной термодинамики нами была предпринята попытка ответов. Для этой цели построили термодинамическую функцию Ляпунова, являющуюся второй вариацией энтропии системы и квадратичной отрицательно определенной формой. По знаку производной такой функции можно судить об устойчивости режимов процесса кристаллизации, а следовательно, о возникновении диссипативных периодических структур, образующихся при потере устойчивости. Также исследовали устойчивость системы вдали и вблизи от равновесия. Производство энтропии системы является мерой устойчивости вблизи равновесия. Оно отражает вклад необратимых процессов и является аддитивной функцией. Для исследуемого процесса кристаллизации производство энтропии (s) вычислялось по формуле: где s1 – вклад необратимых процессов за счет химических реакций; s1 = J1X1 = w*A/T; w = k1 *c1 *c2 – скорость химической реакции; A – химическое сродство реакции; T – температура, s2 = J2X2 = r30r0k1 *((c3-cs)/cs)*RT/T*lnc3/cs – за счет образования кластеров; s3 = J3X3 = r30r0b1 n2 *RT/T*lnn/ns – за счет образования зародышей; s4 = J4X4=r30r0b2 При малых скоростях прилива реагента (при выходе на стационарный режим) производство энтропии системы минимально. Вторая вариация энтропии системы (rd2s) является мерой устойчивости состояния вдали от равновесия и функцией Ляпунова, отрицательно определенной квадратичной формой. Производная от этой функции представляется в виде
где dXi, dJi – вариации термодинамической движущей силы и термодинамического потока необратимого процесса. В связи с этим были исследованы режимы с различной скоростью подачи реагента. В зависимости от изменения расхода фосфита натрия были построены графики изменения во времени концентрации двухосновного фосфита свинца, производной термодинамической функции Ляпунова и производства энтропии. При малых скоростях прилива фосфита натрия процесс выходит на стационарное состояние, и производство энтропии стремится к минимуму в соответствии с теоремой Пригожина о минимуме производства энтропии. С ростом расхода приливаемого реагента можно наблюдать явление бифуркации с удвоением, а затем с учетверением периода. Функция Ляпунова отрицательна, а ее производная положительна, что говорит об устойчивости процесса вдали от равновесия. При хаотическом режиме производная термодинамической функции Ляпунова становится знакопеременной, что свидетельствует о неустойчивости процесса. Средний размер кристалла двухосновного фосфита свинца по ГОСТу должен составлять 10-20 мкм. При небольших расходах фосфита натрия (стационарное состояние исследуемых величин) средний размер кристалла составляет 14 мкм. При регулярных колебаниях этих же величин наблюдается изменение размера кристалла в пределах нормы. В условиях хаотического изменения средний размер кристалла меняется от 3 до 22 мкм, что неприемлемо. Производительность же при небольших расходах фосфита натрия (стационарное состояние) составляет 0.16 кг/час, а при больших (хаотические колебания) – 0.28 кг/час, что является положительным моментом. Поэтому была предпринята попытка регулирования хаотических колебаний концентрации двухосновного фосфита свинца, производной термодинамической функции Ляпунова, производства энтропии при скорости прилива фосфита натрия 3.8 мл/с путем задания расхода фосфита натрия в синусоидальном виде по уравнению: vq=a0[sinwt+0.1] , где a0 =3.8; частоту w подбирали в интервале [p/24-10p] таким образом, чтобы производная r¶/¶td2S сохраняла положительный знак на протяжении всего времени непрерывного ведения процесса. При частоте w=p производная функция d2S (r¶/¶td2S) становилась знакопостоянной и положительной. При циклической подаче реагента при частоте w=p колебания числа кластеров становятся уже не хаотическими, а регулярными. На собственные колебания системы начинают накладываться внешние, вынужденные колебания, приводя колебания к регуляризации. Управление хаотическими колебаниями (при высоких скоростях прилива реагента) можно вести, следя за знакопостоянством (положительным знаком) функции r¶/¶td2S, где основную роль играет избыточное производство энтропии Термодинамический анализ, основанный на использовании метода функций Ляпунова, позволил выявить класс веществ, при кристаллизации которых могут возникать пульсационные, колебательные режимы, а именно класс малорастворимых веществ. Причиной возникновения колебаний, пульсаций является способность системы испытывать и удерживать большие пересыщения, то есть большую удаленность от равновесия. Наличие кластерной теории растворов позволило построить математическую модель кристаллизации труднорастворимого вещества, прогнозирующую пульсационные колебательные режимы при кристаллизации, с учетом образования кластеров, возникновения зародышей кристаллов за счет присоединения кластеров. Дискретная форма записи математической модели процесса кристаллизации в виде логистических уравнений с переменным параметром позволила выявить ряд причин (помимо наличия высокой степени пересыщения) осцилляций при кристаллизации. Причиной возникновения осцилляций концентрации (при большом пересыщении) является конкурентная борьба между источником пересыщения за счет химической реакции и стоком пересыщения за счет образования кластеров. Причиной возникновения осцилляций числа кластеров в растворе (следовательно, осцилляций скорости роста кристаллов) служит борьба между источником образования кластеров и стоком кластеров в образование зародышей и рост кристаллов. Управление хаотическими колебаниями (при высоких скоростях прилива реагента) можно вести, следя за положительным знаком производной термодинамической функции Ляпунова, где основную роль играет избыточное производство энтропии системы. Список литературы 1. Larson M.A., Garside J. Solute clustering and interfacial tension. - J.Crystal Growth, 1986, Vol.76, pp. 88-92. 2. Larson M.A., Garside J. Solute clustering in supersaturated solutions. - Chem.Eng.Sci., 1986, Vol.41, №5, pp. 1285-1289. 3. Khight A.E.W. Cluster: A fifth state of matter? - Chem. Aust., 1991, Vol.58, №8, p.328. 4. Буянов Р.А., Криворучко О.П., Рыжак И.А. Изучение механизма зарождения и роста кристалла гидроокиси и окиси железа в маточных растворах // Кинетика и катализ. - 1972.- т.13. - вып.2. - с. 470-478. 5. Binder K., Stauffer D. Theory for the slowing down of the relaxation and spinodal decomposition of binary mixtures. - Phys. Rev. Lett., 1974, Vol.33, №17, pp. 1006-1009. 6. Фейгенбаум М. Универсальность в поведении нелинейных систем // Успехи физ. наук. - 1983. - Т.141. - №2. - с. 343. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=974 |
Версия для печати Выпуск в формате PDF (1.60Мб) |
| Статья опубликована в выпуске журнала № 1 за 1998 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Оптимизация обработки информационных запросов в СУБД
- Знания в интеллектуальных системах
- Системы баз данных и знаний, разработанные в Республике Куба
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
Назад, к списку статей



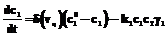 ,
, .
.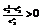
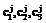
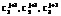
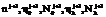
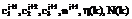
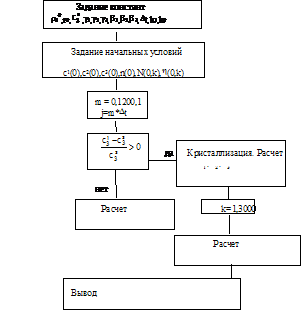
 . (1)
. (1)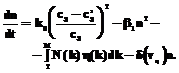
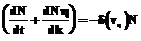 .
.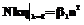 ,
, 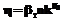 .
.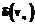 =1 – уравнения системы описывают непрерывный процесс;
=1 – уравнения системы описывают непрерывный процесс; 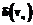 =0 – уравнения системы описывают периодический процесс кристаллизации двухосновного фосфита свинца. Индексы обозначают: 1 – ацетат натрия; 2 – фосфит натрия; 3 – двухосновной фосфит свинца.
=0 – уравнения системы описывают периодический процесс кристаллизации двухосновного фосфита свинца. Индексы обозначают: 1 – ацетат натрия; 2 – фосфит натрия; 3 – двухосновной фосфит свинца.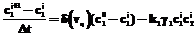 ,
, ,
,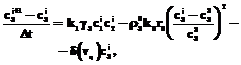
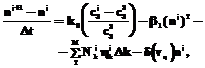 (2)
(2)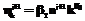 ,
,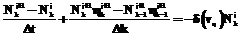 .
. ,
,
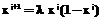 , (3)
, (3)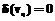 ) процесса кристаллизации двухосновного фосфита свинца параметр логистического уравнения имеет вид:
) процесса кристаллизации двухосновного фосфита свинца параметр логистического уравнения имеет вид: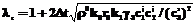 , (4)
, (4)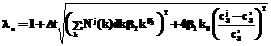 (5)
(5)


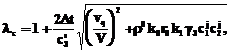
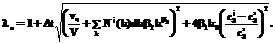 (6)
(6)
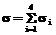 ,
,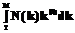 *RT/T*lnn/ns – за счет роста кристаллов, где Xi, Ji – движущая термодинамическая сила и термодинамический поток процесса для i-го компонента.
*RT/T*lnn/ns – за счет роста кристаллов, где Xi, Ji – движущая термодинамическая сила и термодинамический поток процесса для i-го компонента.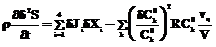 ,
,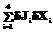 .
.