Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Сравнение сложных программных систем по критерию функциональной полноты
Аннотация:
Abstract:
| Авторы: Хубаев Г.Н. (gnh@donpac.ru) - Ростовский государственный экономический университет (РИНХ), доктор экономических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 17471 |
Версия для печати Выпуск в формате PDF (1.09Мб) |
В настоящей работе объектом рассмотрения являются сложные программные системы (ПС), но описанный алгоритм может применяться для оценки функциональной полноты и других характеристик любых сложных систем, имеющих десятки, сотни и тысячи функций (свойств, признаков, реализуемых услуг и т.п.). Так, ПС, базирующаяся на предложенном алгоритме, успешно использовалась не только по своему основному назначению, но и для формализованного анализа текстов (текстовых файлов). В сегодняшних условиях рынок ПС в состоянии предложить потенциальному покупателю множество систем одного назначения, отличающихся по составу и качеству выполняемых функций (эксплуатационных параметров, характеристик, предоставляемых услуг и др.). Поэтому перед покупателем-пользователем встает проблема выбора из перечня конкурирующих систем одной или нескольких, в наибольшей степени удовлетворяющих его требованиям, например, к функциональной полноте или другим эксплуатационным характеристикам. Если речь идет о программных продуктах (ПП), то для реализации оптимального выбора необходимо, во-первых, располагать количественной оценкой того, насколько (в какой степени) программы-претенденты удовлетворяют конкретным требованиям покупателя-пользователя; кроме того, желательно одновременно определить, какие из нужных пользователю функций не реализуются тем или иным ПП. Во-вторых, и для потребителя, и для конкурирующих фирм-разработчиков ПП важно выявить лучшие по критерию функциональной полноты системы. Желательно также определить перечень функций, реализуемых всеми представленными на рынке ПП. Напомним, что в современных ПП количество выполняемых ими функций (функциональных операций) может достигать нескольких сотен. Очевидно, что в этих условиях вряд ли удастся традиционными методами (вручную) оценить степень соответствия ПП требованиям пользователя, сравнить ПП-претенденты по функциональной полноте. Поэтому в [1,2] для решения подобных задач предложен формализованный подход. Отметим, что за прошедшие годы методика подтвердила прикладную полезность и неоднократно использовалась коллегами и учениками автора. Описанный ниже алгоритм реализовывался с помощью разных инструментальных средств. Здесь мы рассмотрим одну из программно реализованных его модификаций. Алгоритм сравнения. Пусть Z={Zi} (i=1,2,..., n) – множество сравниваемых ПП (ПП-претендентов); R={Rj} (j=1,2,..., m) – множество, составляющее словарь реализуемых ПП {Zi} функций. Исходную информацию представим в виде таблицы {Xij}, элементы которой определяются следующим образом: 1, если j-я функция реализуется i-м ПП. 0, если не реализуется (не выполняется). Xij = Выделим ПП Zi и Zk (i, k = 1, 2,..., n) и введем следующие обозначения:
Для оценки того, какая часть (доля) функций, выполняемых ПП Zi, реализуется также и ПП Zk, можно использовать величину
Взаимосвязь между ПП Zi и Zk оценивается по значениям
где Выбирая различные пороговые значения e элементов матриц P, G и H, можно построить логические матрицы поглощения (включения) P0, G0, H0. Например, элементы матрицы H0 получают следующим образом: 1, если 0, если Граф, построенный по логическим матрицам P0, G0, H0, дает наглядное представление о взаимосвязи между сравниваемыми ПП (по выполняемым функциям). Строку с перечнем функций, которые интересуют пользователя (должны выполняться ПП-претендентом), обозначим через Ze. Дополнив таблицу {Xij} (iÎn, jÎm) строкой Xej (jÎm), рассчитаем матрицы P(10), P(11). Затем, выделив строки, у которых Последовательность шагов реализации алгоритма 1) В справочнике функций, выполняемых сравниваемыми ПП, отмечаются те функции (функциональные операции), которые должны выполняться условным (реально не существующим) ПП, и формируется новая строка Ze. Этой строкой дополняется исходная таблица {Xij}, то есть в таблице Zi = {Xij} появляется строка Ze (iÎ(n+1), jÎm). Строятся матрицы (i, jÎn+1). 2) В матрицах Pij или Hij (i, jÎn+1) выделяются строки Pej и Hej (jÎn+1). 3) Из n элементов Zi, каждый из которых соответствует одному из рассматриваемых ПП, выбираются только те, у которых Предположим, что число удовлетворяющих этому условию программных пакетов равно d, dÌ n. 4) Формируется новая матрица 5) Для подмножества 6) По матрице Таблица А
Из таблицы А пользователь выбирает одну или несколько заинтересовавших его функций, которыми дополняется строка Ze, после чего процесс повторяется, начиная с шага 2. 7) По матрице
Легко убедиться, что даже в таком простейшем случае (n=6, m=15) сравнение и оптимальный выбор ПС по критерию функциональной полноты осуществить весьма не просто. Но ведь ситуации, когда n, m > 100 вполне обычны. Поэтому анализ будем проводить, следуя предложенному ранее алгоритму. Сначала для таблицы 1 вычислим матрицы P(01), G и H, а затем построим логические матрицы поглощения P0(01), G0 и H0, выбрав следующие пороговые значения элементов:
и eh=1(i,kÎn). P(01)= H= G0 = Предположим теперь, что для потребителя-пользователя нужно, чтобы ПС-претендентом выполнялись функции R2, R5, R6, R10. Обратившись к построенным матрицам, обнаружим, что интересующие пользователя функции реализуются тремя ПС: Z1, Z3, Z4 (см. четвертый столбец матрицы P(P0) или четвертую строку матрицы H(H0)). Что касается ПС Z2, Z5, Z6, то в них нужные пользователю функции реализованы лишь частично. Продолжая действовать в соответствии с описанным алгоритмом, легко ответить на все основные вопросы, возникающие при количественной сравнительной оценке ПС по критерию функциональной полноты. Область применения, преимущества. Нам не известны другие алгоритмы и методики, позволяющие с меньшими затратами финансовых и интеллектуальных ресурсов осуществить следующее: 1) составить полный перечень функций, реализуемых всеми представленными на рынке ПП; 2) систематизировать сведения о составе и функциональной полноте существующих ПП; 3) количественно оценить степень соответствия того или иного ПП требованиям пользователя к функциональной полноте; 4) проранжировать ПП по критерию функциональной полноты; 5) на стадии предварительного анализа исключить из дальнейшего рассмотрения ПП, в которых не реализуются нужные пользователю функции; 6) сформировать группу ПП, имеющих одинаковую функциональную полноту, сопоставить их цены и другие характеристики; 7) расширить для потребителя-пользователя возможности оптимального выбора на рынке программных средств, предоставив перечень выполняемых каждым ПП функций, а разработчику ПП показать место его продукта среди существующих ПС и одновременно дать первоначальную оценку конкурентным рыночным позициям фирм-разработчиков ПП. Список литературы 1. Хубаев Г.Н. Анализ информационных потребностей пользователей при создании АРМ // Автоматизированные рабочие места в системе управления предприятием. - Л.: ЛИЭИ, 1989. 2. Хубаев Г.Н. Методика анализа предметной области // Компьютеризация информационных процессов в управлении народным хозяйством. - М.: МЭСИ, 1988. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=978 |
Версия для печати Выпуск в формате PDF (1.09Мб) |
| Статья опубликована в выпуске журнала № 2 за 1998 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Спецификация объектно-ориентированной модели данных с помощью отношений
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Автоматизированная система принятия решений при стратегическом планировании устойчивого развития региона в условиях нечеткой информации
Назад, к списку статей



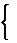
 – число функций, выполняемых и Zi, и Zk, то есть
– число функций, выполняемых и Zi, и Zk, то есть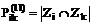 – мощность пересечения множеств Zi={Xij} и Zk={Xkj} (jÎm;
– мощность пересечения множеств Zi={Xij} и Zk={Xkj} (jÎm;  );
);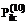 – число функций, выполняемых ПП Zi, но не реализуемых ПП Zk, то есть
– число функций, выполняемых ПП Zi, но не реализуемых ПП Zk, то есть  – мощность разности множеств Zi = {Xij} и Zk = {Xkj};
– мощность разности множеств Zi = {Xij} и Zk = {Xkj};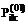 – число функций, выполняемых ПП Zk, но не реализуемых ПП Zi, то есть
– число функций, выполняемых ПП Zk, но не реализуемых ПП Zi, то есть  – мощность разности множеств Zk и Zi;
– мощность разности множеств Zk и Zi; – мощность объединения множеств Zi и Zk, то есть
– мощность объединения множеств Zi и Zk, то есть 
 .
.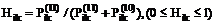 .
.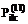 и
и ,
,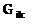 – мера подобия Жаккарда.
– мера подобия Жаккарда.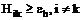
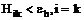

 либо
либо  получим перечень ПП, полностью удовлетворяющих требованиям пользователя к функциональной полноте программного средства (или любой другой сложной системы).
получим перечень ПП, полностью удовлетворяющих требованиям пользователя к функциональной полноте программного средства (или любой другой сложной системы). Hij
Hij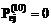 или Hej=1 (jÎn), то есть ПП, которые включают в качестве подмножества перечень функций, реализуемых условным ПП Ze.
или Hej=1 (jÎn), то есть ПП, которые включают в качестве подмножества перечень функций, реализуемых условным ПП Ze. (iÎd).
(iÎd).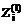 (iÎd) строится матрица
(iÎd) строится матрица 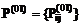 (i, jÎd).
(i, jÎd).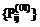 последовательно для
последовательно для  и т.д. строится таблица А, в которой перечисляются функции, не предусмотренные в условном пакете Ze, но реализуемые пакетом Zj (jÎd).
и т.д. строится таблица А, в которой перечисляются функции, не предусмотренные в условном пакете Ze, но реализуемые пакетом Zj (jÎd).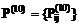 последовательно для
последовательно для  и т.д. строится таблица В, аналогичная таблице А, в которой перечисляются функции, предусмотренные в Ze, но не реализуемые пакетом Zj, а по матрицам
и т.д. строится таблица В, аналогичная таблице А, в которой перечисляются функции, предусмотренные в Ze, но не реализуемые пакетом Zj, а по матрицам  для выбранных пороговых значений e их элементов можно выделить и представить в виде таблицы подмножества общих (или часто реализуемых) функций, оценить степень взаимосвязи между изучаемыми ПП по выполняемым функциям и т.д.
для выбранных пороговых значений e их элементов можно выделить и представить в виде таблицы подмножества общих (или часто реализуемых) функций, оценить степень взаимосвязи между изучаемыми ПП по выполняемым функциям и т.д.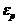 = 1(
= 1(

 ; P0(01) =
; P0(01) =  ;
; ;
; ; H0 =
; H0 = .
.