Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Прогнозирование эффективности систем хранения информации
Аннотация:
Abstract:
| Авторы: Куракин А.Л. (a.kurakin@inbox.ru) - Институт океанологии им. П.П. Ширшова РАН, г. Москва, доктор физико-математических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11314 |
Версия для печати Выпуск в формате PDF (1.09Мб) |
Современное развитие сетевых средств обо- стрило известную проблему защиты информации от несанкционированного доступа. После того как специалисты, работающие в наукоемких областях, уже перевели основную часть своих рабочих документов в компьютерный вид, подключенные к сети компьютеры превратились в потенциальный объект исследования всевозможных сетевых хакеров. Поэтому самые актуальные идеи могут быть теперь просто похищены у автора в тот период, пока рабочие материалы еще "витают" в памяти его компьютера. И если прежде речь шла о вложениях в развитие средств информатики, то теперь необходимы затраты на защиту информации. По известным данным в США на это тратится 10 млрд. долларов в год. Для выработки оптимальной стратегии материальных вложений принципиальное значение имеет критерий различения удач и неудач в работе системы защиты. В существующей практике за неудачи в обеспечении информационной безопасности принимаются, например, те случаи потерь информации, при которых ущерб превышает затраты. При всем удобстве привычного денежного эквивалента в данном случае остается проблема той неопределенности оценки ущерба, которая наиболее существенна и принципиальна именно в отношении интеллектуальной продукции. Действительно, ущерб от утраты уникальной информации подобного рода может оцениваться и потерями средств на ее создание (разработку), и более трудно определимыми потерями, связанными с фальсификацией новизны идеи (с потерей приоритета), и совсем уже приблизительными (хотя, возможно, и весьма значительными) последствиями в государственной экономике, в технологии или, наконец, еще более предположительными (но еще более фатальными) последствиями глобально-политического или военно-стратегического характера. Происхождение этих неопределенностей в оценках реального ущерба вполне объяснимо: похищение информации разрушает также и некоторые планы по ее использованию или развитию научно-технической разработки. И в смысле учета значимости подобного рода контекстов или содержания метаинформации, находящейся за пределами конкретных похищаемых файлов, строгие теоретические оценки вряд ли будут возможны. Однако и в самом общем случае несомненным остается тот факт, что ценность информации связана с существованием некоторой цели. И эффективность информационной системы наиболее естественно было бы оценивать с точки зрения достижимости соответствующей цели. Хранимая информация предполагается необходимой для достижения цели, но в то же время, возможно, и недостаточной. Даже полностью оформленная техническая документация к моменту ее превращения в компьютерную форму хранится уже не столько с (промежуточной) целью изготовления некоторого объекта, но уже с целью получения определенных преимуществ от его производства или использования. С точки зрения окончательной цели хранимую информацию не следует полагать исчерпывающей, а скорее рассматривать ее как некие рабочие материалы. Надо полагать, что информацию вообще приходится хранить постольку, поскольку определенную проблему не удается решить сразу. И тогда задача защиты информации сводится к тому, чтобы сохранить ее от несанкционированного доступа до того момента, когда ее можно будет рассекретить, уничтожить, видоизменить и т.п. Таким образом, наряду с фактом конечной надежности защиты надлежит учитывать и конечную продолжительность существования той конкретной задачи, ради которой сохраняется и оберегается соответствующая связная информация. И это обстоятельство позволяет решать задачу оптимальной стратегии информационной защиты как вероятностную задачу успевания. Оценивается вероятность того, что цель, ради которой информация хранится, удастся достигнуть раньше, чем произойдет утечка. Общее выражение для этой вероятности может быть представлено интегралом вида [1] P(T) = где P(T) – вероятность того, что в течение времени T цель будет достигнута ранее, нежели произойдет утечка информации; R(t) – вероятность надежности системы во времени t, представляющая вероятность того, что утечки не произойдет до момента t; s(t) – плотность распределения вероятности случайного момента достижения цели во времени t. Различия в обозначении времени (переменными t и T) будем полагать чисто формальными (обозначение t используется в подынтегральных выражениях). Будучи априорной оценкой ожидаемой результативности, функция P(T) может рассматриваться как прогноз эффективности работы с информационной системой во времени T. Так что реализуемость и достоверность этого прогноза далее зависит уже от возможности получения обоснованных выражений для подынтегральных функций s(t) и R(T). Аналитическое выражение результативности научно-технических разработок Изложим способ вывода функций для описания продолжительности процессов работы с информацией, то есть функций вероятности времени достижения цели. Будем рассматривать такие работы (типа целевых научных исследований, разработки наукоемких технологий и тому подобных рабочих процессов), для которых определена конечная цель и известны промежуточные этапы, необходимые и достаточные для ее достижения. То есть момент достижения цели можно представить как сложное событие, состоящее из последовательности событий успешного завершения этапов. Ограничивая представление о рабочем (интеллектуальном) процессе столь общими признаками, как наличие цели и поэтапное ее достижение, мы можем относить к ним (или к их этапам) и те действия с информацией, которые по существу совершаются за пределами компьютерной системы другими средствами и методами, в том числе и неформализуемыми. Исходя из такого общего вербального описания интеллектуальных процессов, переход к детерминированной математической модели был бы весьма проблематичен. Более естественными оказываются тут вероятностные представления. В данном случае можно заметить, что чем больше неопределенность (непредсказуемость) планируемой работы, тем больше оснований (то есть тем естественнее) представить каждый этап в виде последовательности попыток. Если обозначить случайное состояние ji
представляет этап, выполнение которого потребовало времени t (то есть этап, завершившийся за t дискретных шагов). При условии независимости попыток, характеризующихся постоянной вероятностью a успеха, функция распределения S(t) случайного времени t продолжительности этапа (S(t) º S{t³t}) может быть представлена в виде S(t) = 1-(1-a)t (3) для дискретного t. При переходе к непрерывному времени t, функция S(t) принимает вид экспоненциального распределения S(t) = 1-exp (-at) (4) с плотностью вида s(t) = a exp(-at), (5) где a – вероятность успеха в единицу времени. Тот факт, что распределением вероятности времени достижения цели является экспоненциальное распределение, в более подробном и общем виде доказывается в теории потенциальной эффективности сложных систем [2] (где экспоненциальное распределение оказывается предельным законом внешней эффективности). Характерной особенностью экспоненциального распределения (именуемого также показательным и геометрическим) является так называемое отсутствие последействия. Данное свойство в нашем случае является формальным отражением того факта, что до тех пор, пока этап не завершен, вложенные усилия (затраты, выраженные во времени или числе попыток) никаким видимым образом не приближают результат. Результат либо есть, либо его нет. Это значит, что если бы в момент времени t1>0 можно было проверить состояние процесса и узнать, например, что результата нет, то в функции (4) следовало бы принять этот момент за новое начало отсчета, то есть положить t1=0. Отсутствие последействия в нашем случае соответствует поиску решения среди неограниченного числа вариантов. Перейдем к соответствующим формальным выражениям. Очевидно, что случайная продолжительность поэтапных работ, представляющая собой сумму продолжительностей этапов, может быть выражена посредством сверток или производящих функций. В предположении равной трудности n этапов (каждый из которых характеризуется параметром a=d) продолжительность всей работы может быть описана функцией Sn(t) = 1-exp(-dt) Выражение (6) доказывается для экспоненциального распределения методом индукции [3, с 24]. В случае неравных dj и dk на различных этапах может быть использовано выражение функции sn (t) плотности вида s n(t) = d0 ... dn-1[y0,n exp(-d0t) +... ...+ yn,n exp(-dnt)], (7) где yk,n=[(d0 - dk) ... (dk-1 - dk)(dk+1 - dk)... ...(dn - dk)]-1 (8) (см. пример 12 в [3, с. 56]). Заметим, что аналогичные общие свойства (последовательность этапов, перебор вариантов на каждом этапе) характерны и для действий противной стороны, стремящейся воспользоваться чужой информацией. Действительно, эта задача предполагает не только доступ к чужой системе – во-первых, но и, возможно, необходимость дешифрации считанных файлов – во-вторых и, наконец, в-третьих, после того как информация сделана читаемой, ею еще надлежит воспользоваться уже по существу (идентифицировать проблему, оценить решение, найти применение, при неполноте разработки завершить ее и т.п.). При этом общий вид функции распределения L(t) и l(t) (плотности распределения) времени t утечки информации имеет вид, аналогичный виду функции S(t) с распределением s(t). Функция R(t) надежности представляет вероятность, дополнительную к вероятности L(t): R(t) = 1 - L(t) (9) (надежность защиты информации буквально означает безуспешность попыток несанкционированного доступа). Используя аналогичность вида функций L(t) и S(t), а также соотношение (9), для функции R(t) надежности в простейшем случае (одноэтапного доступа) имеем выражение вида R(t) = exp(-lt), (10) где l – вероятность несанкционированного доступа в единицу времени. Интерпретации и примеры Рассмотрение практических примеров естественно начать со случая минимального числа параметров, то есть с того случая, когда основные действия по использованию информации являются одноэтапными. При этом функция s(t) плотности распределения и вероятность R(t) надежности определяются соотношениями вида (5) и (10) соответственно. Подставляя (5) и (10) в основное выражение (1), имеем после интегрирования P(T) =
Для анализа поведения функции в области малых и больших периодов времени T, перейдем к приближенному равенству
P(T)» Основной практический интерес представляет, по-видимому, вопрос об эффективности достаточно продолжительного хранения информации. Из выражения (12b) следует, что эффективная работа с информацией (то есть тот случай, когда P(T) приближается к единице) возможна при условии a»l. При таких условиях величина P(T) приближается к предельному значению
Соотношение (13) можно учитывать при определении общей стратегии работ. Повышение их эффективности возможно не только путем защиты информации (то есть уменьшением l), но и путем интенсификации работ по данной теме (увеличением a). Зная характер зависимостей a и l от соответствующих затрат, можно решать задачи оптимизации последних. Рассмотрим частные случаи, которые не требуют знания таких зависимостей. Дублирование. Если одна и та же информация находится в работе у n равносильных соавторов (соисполнителей) в полном виде, то параметр a связан с параметром a1 одного соисполнителя простым соотношением a1 = n a1. (14) Что же касается параметра l, то тут возможны варианты. Если защиты систем всех соисполнителей одинаковы, то, полагая, что доступ в одну из персональных систем есть доступ к рассматриваемой информационной системе, то очевидно совпадение параметров: l = l1. (15) С другой стороны, возможны и такие ситуации, когда существование нескольких (n) копий повышает вероятность несанкционированного доступа; при этом крайний случай представляет пропорциональное повышение l, то есть l = n l1. (16) Подставляя в формулу (11) соотношения (14) и, например, (16), получаем выражение P(T)= Появление коэффициента n перед переменной T времени имеет довольно очевидный смысл “сжатия” времени эквивалентно n-кратной интенсификации работ. В этом случае распространение работы среди возможных соавторов повышает вероятность ее успешного завершения. Можно заметить, что хотя предположение о пропорциональной интенсификации (14) может быть излишне оптимистичным, однако и предположение о пропорциональном возрастании опасности l ((16) – наихудший случай) можно полагать излишне пессимистичным. Более строгий анализ зависимости эффективности от a и l связан с задачей об оптимальном распределении затрат. Здесь же достаточно отметить, что дублирование разработок в принципе может рассматриваться как один из вариантов повышения эффективности. Задача оптимального распределения ресурсов Очевидно, что, говоря о работе с информационными системами, надлежит различать два следующих вида обеспечения, характеризующих состояние системы с принципиально различных точек зрения. 1. Универсальная (не зависящая от смыслового содержания информации) техника, обеспечивающая защиту информации. 2. Специальное обеспечение работ по существу той проблемы, ради которой данная информация хранится в системе. Положим, что усилия (затраты) во времени t на первый вид обеспечения информационной системы приводят к тому, что вероятность потери (утечки) информации в соответствующие моменты времени характеризуются функцией l(t). Аналогичным образом усилия (затраты) на специальное обеспечения работ с информацией характеризуются во времени функцией a(t). Заданные функции a(t), l(t) определяют соответствующие функции S(t) (s(t)=S'(t)) и L(t) R(t) = 1 - L(t), которые могут быть получены как решения уравнений вида
с разделяющимися переменными [4, с. 25], решения которых имеют вид S(t) = 1 - exp L(t) = 1 - exp где постоянная интегрирования равна нулю. Подстановка s(t)=S'(t) и R(t)=1-L(t) в выражение (1) приводит к получению функции эффективности в виде P(T)= или P(T)= являющейся обобщением выражения (11) на случай изменяющихся во времени a и l. По известным зависимостям a и l от затрат может ставиться задача оптимизации системы, например задача минимизации затрат при заданных порогах Pmin и Tmax значений P(T) и T. Возможна также максимизация P(T) при заданных суммарных затратах на соответствующего вида обеспечение (задача об оптимальном распределении ресурсов). Во всяком случае выражение (19) дает возможность численных оценок, уже позволяющих прогнозировать эффективность. Список литературы 1. Куракин А.Л., Флейшман Б.С. Два варианта функции осуществимости. //Автоматика. -1984. -№ 2. -С. 81-82. 2. Флейшман Б.С. Элементы теории потенциальной эффективности сложных систем. -М.: Сов. радио, 1971. -224 с. 3. Феллер В. Введение в теорию вероятностей и ее приложения. Ч.2. -М.: Мир, 1984. -752 с. 4. Степанов В.В. Курс дифференциальных уравнений. М.-Л.: ГОНТИ. -1939. -384 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=980 |
Версия для печати Выпуск в формате PDF (1.09Мб) |
| Статья опубликована в выпуске журнала № 2 за 1998 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Методы восстановления пропусков в массивах данных
- Анализ российского и зарубежного рынков программных продуктов
- Интерактивная процедура построения модели тренда для экономических показателей
- Спецификация объектно-ориентированной модели данных с помощью отношений
- Общедоступные математические САПР для персональных компьютеров класса IBM PC
Назад, к списку статей



 s(t)R(t)dt, (1)
s(t)R(t)dt, (1) подпроцесса (этапа) в дискретные моменты времени i (i=1,2,...,t) альтернативными значениями a (успех) и
подпроцесса (этапа) в дискретные моменты времени i (i=1,2,...,t) альтернативными значениями a (успех) и 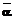 (неудача), то последовательность вида
(неудача), то последовательность вида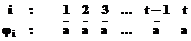 (2)
(2)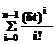 . (6)
. (6) [1-exp(-(l+a)T)]. (11)
[1-exp(-(l+a)T)]. (11)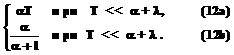
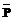 , имеющему вид
, имеющему вид . (13)
. (13)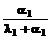 [1 - exp(-(
[1 - exp(-( ) nT)]. (17)
) nT)]. (17)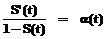 , (18a)
, (18a)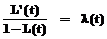 , (18b)
, (18b) , (19a)
, (19a)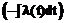 , (19b)
, (19b)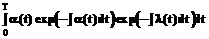 (20a)
(20a) , (20b)
, (20b)