Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программный комплекс прогнозирования параметров экономической динамики региона
Аннотация:
Abstract:
| Авторы: Колесник Г.В. () - , Катулев А.Н. (katulevan@yandex.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 8806 |
Версия для печати Выпуск в формате PDF (1.09Мб) |
В настоящее время для органов управления являются актуальными задачи прогнозирования состояния экономической системы в будущем. Для этой цели разработаны и продолжают разрабатываться различные математические модели. Наиболее перспективными из них представляются модели, основанные на межотраслевых балансах, так как они могут обеспечивать достаточную детализацию и отвечать на широкий спектр вопросов практики управления [1 - 4]. В настоящей статье описывается динамическая модель многоотраслевой производственно-экономической системы региона, предназначенная для прогнозирования основных ее параметров. Она базируется на математической модели [4, 5] и полностью ориентирована на проведение исследований экономической динамики региона в рыночных условиях. Ее особенностями, в отличие от [5], являются учет условий несовершенной конкуренции в системе, что характерно для товарных рынков регионов России в настоящее время [6], а также механизмов межотраслевого перелива капитала в зависимости от прибыльности отраслей промышленности. Каждый экономический субъект описывается в модели отдельно как имеющий свой критерий оптимальности поведения, представляющий собой интеграл от функции полезности (для потребителей) либо дохода (для производителей и торгово-посреднических фирм). Взаимосвязи между производителями описываются матрицей межотраслевого баланса, которая предполагается продуктивной. Объемы продукции, выпускаемой промышленностью, определяются производственными функциями отраслей, а объемы конечного потребления – функциями спроса, предполагающимися вогнутыми. Задача прогнозирования состояния экономической системы представляется в модели в виде иерархической динамической операции нескольких сторон [7], в которой управляющие органы образуют верхний уровень иерархии, а остальные экономические субъекты действуют без коалиций. Поэтому отыскание траектории сбалансированного развития экономической системы сводится к отысканию положения динамического равновесия в данной иерархической игре. Теорема 1. В экономической системе, удовлетворяющей указанным выше условиям, существует положение равновесия.
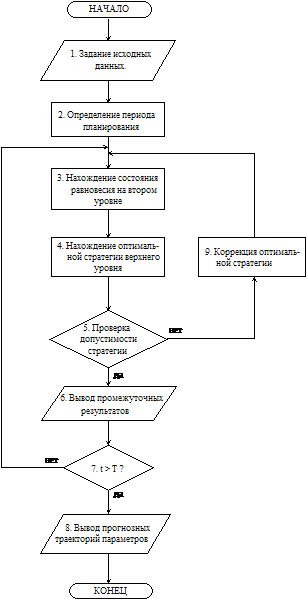
В качестве исходных данных для работы модели приняты: - межотраслевые потоки продукции в виде матрицы межотраслевого баланса (МОБ); - величины основных производственных фондов (ОПФ) отраслей промышленности и численность работающих в них на начало периода прогнозирования; - коэффициенты производственных функций отраслей промышленности; - величины заработной платы производственных рабочих; - коэффициенты амортизации основных производственных фондов; - информация о внешних рыночных ценах на продукцию отраслей промышленности; - величины ставок налогов, собираемых с предприятий промышленности органами управления местного и федерального уровней; - коэффициенты функций спроса потребителей на отраслевую продукцию; - коэффициенты функций, описывающих распределение инвестиций по отраслям промышленного комплекса. Работа модели осуществляется согласно блок-схеме (рис. 1). В блоках 1 и 2 производится задание исходных данных по приведенному списку и определяется временной интервал, на котором будет строиться прогноз. В блоках 3, 4 для каждого временного сечения при помощи итерационного метода вычисляется состояние иерархического равновесия для исследуемой экономической системы. Полученные значения параметров проверяются на допустимость (5) и при необходимости корректируются с учетом ограничений (9), а затем записываются в файл промежуточных результатов (6). В блоке 7 проверяется условие достижения конца интервала прогнозирования, и в случае его выполнения происходит построение траекторий параметров системы (8). В ходе вычислительных экспериментов с моделью была подтверждена сходимость получаемых траекторий к некоторому стационарному значению, доказанная аналитически. Теорема 2. Пусть j = (j1, j2, ..., jn) – некоторая стратегия распределения инвестиций, зависящая только от норм прибыли отраслей промышленности r = (r1, r2, ..., rn), для которой выполнены следующие условия: 1. если ri = 0, то ji(r) = 0; 2. j – симметрична, то есть, если ri = rj, то ji(r) = jj(r). Тогда для экономической системы имеет место такой стационарный режим, на котором нормы прибыли функционирующих отраслей положительны (отрасли рентабельны) и равны между собой.
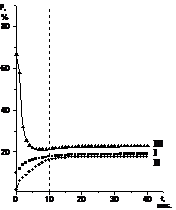
Количественные значения параметров системы на данном режиме не зависят от начальных условий, а определяются только структурой межотраслевых связей в системе и динамикой цен на внешнем рынке. Таким образом, стационарный режим обладает некоторыми магистральными свойствами. Кроме того, он является оптимальным в том смысле, что все отрасли промышленного комплекса системы развиваются сбалансированно и имеют одинаковую норму прибыли. Программный комплекс, реализованный на базе данной модели, вычисляет по наборам исходных данных значения параметров системы для стационарного режима, а также траектории перехода системы в данный режим. На рисунке 2 представлены результаты численных расчетов, проведенных на разработанном программном комплексе для трехотраслевой экономической системы, при следующих исходных данных: – матрица МОБ: – величины ОПФ отраслей на начальный момент времени (млрд. р.): Ko = (35.00, 60.00, 10.00); – коэффициенты амортизации (%): m = (20.0, 20.0, 20.0); – численность производственных рабочих на начальный момент (тыс. чел.): Lо = (0.90, 1.50, 1.00); – величины зарплаты (млрд. р./тыс. чел.): w = (0.30, 0.30, 0.30); – производственные функции отраслей заданы в виде функций Кобба-Дугласа с коэффициентами a = (0.40, 0.50, 0.50); – величины внешних цен на продукцию (тыс. р.): q = (20.0, 18.0, 30.0); – функции спроса – линейные, с коэффициентами (эластичность цен по выпуску продукции) l = (0.20, 0.25, 0.30); – доля инвестиций, идущая в отрасль, Интервал прогнозирования для расчетов брался равным T = 40 месяцев. Видно, что за время t*, составляющее около 10 месяцев, изучаемая система выходит на стационарный режим функционирования, характеризующийся существенным изменением пропорций основных производственных фондов отраслей, а также выравниванием значений норм прибыли r и их сходимостью к величине порядка 20 %. Описанный программный комплекс оформлен в виде блока, генерирующего информацию о равновесном состоянии экономической системы, и может применяться в составе системы поддержки принятия решений по прогнозированию основных показателей экономической динамики отдельного региона. Определение стационарного режима функционирования промышленного комплекса позволяет оценивать текущие экономико-производственные показатели с точки зрения долговременной перспективы развития, а также прогнозировать величины его параметров при изменениях внешних условий в будущем. Список литературы 1. Иванов Ю.Н., Токарев В.В., Уздемир А.П. Математическое описание элементов экономики. - М.: Наука, 1994. 2. Петров А.А. Экономика. Модели. Вычислительный эксперимент. - М.: Наука, 1996 3. Черемных Ю.Н. Анализ поведения траекторий динамики народно-хозяйственных моделей. - М.: Наука, 1982. 4. Основы теории оптимального управления. / Под ред. В.Ф. Кротова. - М.: Высшая школа, 1990. 5. Катулев А.Н., Колесник Г.В. Программный комплекс оптимизации основных показателей развития отраслей промышленности. // Программные продукты и системы. - 1997. - № 2. 6. Гурков И., Авраамова Е. Стратегии выживания промышленных предприятий в новых условиях // Вопросы экономики. - 1995. - № 6. 7. Arunabha Bagchi. Stackelberg Differential Games in Economic Models // Lecture Notes in Control and Information Sciences. vol. 64. Springer-Verlag, 1984. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=984 |
Версия для печати Выпуск в формате PDF (1.09Мб) |
| Статья опубликована в выпуске журнала № 2 за 1998 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Базовое программное обеспечение целостных компьютеризированных курсов в современной операционной обстановке
- Автоматизированная система принятия решений при стратегическом планировании устойчивого развития региона в условиях нечеткой информации
- Автоматизированное рабочее место расчета стоимости эксплуатации кораблей
- Подход к выбору оптимального маршрута при перевозке крупногабаритных грузов на основе нейросетевых технологий
- Инженерная программа трехмерного моделирования магнитных систем LittleMag
Назад, к списку статей



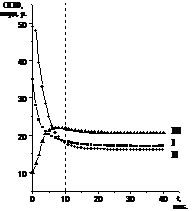
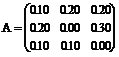 ;
;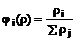 , пропорциональна ее прибыльности.
, пропорциональна ее прибыльности.