Декомпозиционный алгоритм оптимизации многопродуктовых химико-технологических систем
| Макаров В.В. (l.s.gordeev@yandex.ru) - Российский химико-технологический университет им. Д.И. Менделеева, Москва, Россия, доктор технических наук, Гордеев Л.С. (l.s.gordeev@yandex.ru) - Российский химико-технологический университет им. Д.И. Менделеева, Москва, Россия, доктор технических наук, Сбоева Ю.В. () - , Иленева Е.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Многопродуктовые химико-технологические системы относятся к классу сложных технологических объектов, частично-дискретная задача оптимизации которых имеет большую размерность, что существенно затрудняет разработку эффективных алгоритмов. Универсальным приемом решения таких задач является декомпозиционный подход [3,5,7]. Однако специфика многопродуктовых химико-технологических систем, технологическое оборудование которых работает в периодическом существенно нестационарном режиме, а аппаратурная структура изменяется при смене ассортимента выпускаемых продуктов, не позволяет непосредственно применить опубликованные в литературе алгоритмы, которые в основном построены на основе упрощенных структурно-функциональных моделей и ориентированы на так называемые “модельные” системы. Разработанные в последнее время алгоритмы оптимизации упомянутых систем [8-11,13,14] основаны на модификациях декомпозиционного метода Бендерса [7], его обобщениях и модификациях [10] так называемой внешней аппроксимации [8] в сочетании с процедурой релаксации Джоффриона [10,11]. Перечисленные алгоритмы разрабатывались при наиболее простых критериях оптимальности, в качестве которых принимались капитальные затраты. Ниже описан разработанный авторами декомпозиционный алгоритм оптимизации многопродуктовых химико-технологических систем, учитывающий их специфику и ориентированный на системы реальной степени сложности для сепарабельного критерия – приведенных затрат. ЗАДАЧА ОПТИМИЗАЦИИ Сформулируем задачу оптимизации гибких химико-технологических систем в общей постановке. Пусть требуется произвести I продуктов в количестве Gi, i= СТРУКТУРНО-ФУНКЦИОНАЛЬНАЯ МОДЕЛЬ Излагаемая методология формирования моделей многопродуктовых химико-технологических систем основана на стратегии системного анализа, согласно которому образующие сложную систему подсистемы рассматриваются как элементы систем более высокого уровня, а ее модель формируется путем стратификации исследуемой системы, состоящей в выделении однопорядковых элементов, образующих соответствующие им иерархические уровни. Формирование модели системы произвольного уровня осуществляется объединением моделей подсистем непосредственно нижележащего уровня с помощью координирующего соотношения.
Рис. 1. Структура модели многопродуктовых химико-технологических систем: må - обобщенная модель многопродуктовой химико-технологической системы; mSa ; a= mAab ; a= mOabf ; a= ePabfq ; a= cpo - модель, координирующая уровни “физико-химический процесс – технологическая операция”; cOA - модель, координирующая уровни “технологическая операция – аппарат”; cAS - модель, координирующая уровни “аппарат – индивидуальная система”; cSå - модель, координирующая уровни “индивидуальная система – многопродуктовая система”. Многопродуктовая химико-технологическая система, рассматриваемая с общесистемных позиций, представляет собой многоцелевую (целеориентирован-ную) адаптивную систему, цели функционирования которой генерируются внешней по отношению к ней системой (средой). Изменение ассортимента производимой продукции порождает модификации структуры системы. В пределах некоторого интервала времени система реализует конкретную цель – производство продукции фиксированного ассортимента, которому соответствует определенный вариант ее структуры. Структура модели химико-технологической системы периодического действия схематично представлена на рисунке 1, на котором изображены модели ее подсистем и модели-координаторы. Сформируем структурно-функциональную модель многопродуктовой химико-технологической системы. Определим сначала ограничения, налагаемые на структуру системы, введя массив структурных параметров X, являющихся булевскими переменными: 1, если стадия j получения продукта i в xijkl = í группе k выполняется в аппарате типа l (1) 0 – в противном случае Каждая стадия получения каждого продукта должна быть реализована по крайней мере в одном аппарате и в одной серии:
Количество типов аппаратов, назначенных стадии j получения продукта i в серии k, не может превышать общее количество аппаратов типа l:
Аппаратура, предназначенная для некоторой стадии технологического процесса, должна принадлежать к одному и тому же параметрическому ряду, а аппараты разных размеров не могут объединяться в блоки: xijkl + xijde £ 1 , (4) i= Следующее ограничение запрещает использование технологических аппаратов для реализации более чем одной стадии получения конкретного продукта: xijkl + xij+1,ke + xij-p,ke £ 2 , i= eÎ{Aj+1,i ÇAj-p,i }; lÎDf; eÎDq; f¹ q . (5) Кроме приведенных выше, система ограничений содержит следующие ограничения, смысл которых очевиден: gi,k £
Nl ³ å Pijk × Qijkl ; lÎ Aij ; k = Pijkl £ Nlmax xijkl ; i= Pijkl £ xijkl ; i= Qijk £ Qijk max× tLik ³ xijkl × tLik ³tLikmax ×
Tk £ nik× tLik; i= Vl = Nl = Pijkl = Qijk = Кроме того: 0 £ Tk £ T0 , ; k=
uijkl* = qijkl = НОК (tij-1,kl ,tijkl ); (24) 0 £ Dtijkl < ¥ , (25) utijkl(t,Dtijkl)³0, (26) t0ijkl £ t£¥ , (27) где t0ijkl – момент начала первой загрузки демпфирующей емкости. Вид функций uijkl(t) зависит от режимов работы взаимодействующих аппаратов [4]. Объем реакционной массы, содержащейся в аппарате периодического действия, определяется в результате решения уравнений материального баланса и баланса объемов реакционной массы в аппаратах, взаимодействующих через демпфирующие емкости. Материальный и тепловой балансы аппаратов периодического действия имеют вид:
cijkl(0)=c0ijkl; i= tijkl ={tijkl | cii’jklh = cii’jkl*h}. (30) Баланс объемов реакционной массы для аппаратов, взаимодействующих через демпфирующие емкости, имеет вид: nijkl × tijkl = nij-1,kl × tij-1,kl . (31) Откуда: nijkl = где i= Условие (31) позволяет вычислить nijkl по известной величине nij-1,kl , которая определяется из уравнений материального баланса для последнего по ходу технологического потока аппарата по формуле: niJkl = Концентрация cijkl находится из уравнений (28) при граничных условиях (29). КРИТЕРИЙ ОПТИМАЛЬНОСТИ Примем в качестве критерия оптимальности приведенные затраты CП(X,Y,Z,W), как наиболее полно отражающие издержки на производство продукции [2]. Для того чтобы было возможно применить декомпозиционный алгоритм, критерий оптимальности должен быть сепарабельным. Критерий CП(X,Y,Z,W) можно представить в виде суммы распределенных по уровням иерархии составляющих, зависящих соответственно от X, Y, Z и W: CП(X,Y,Z,W)= CП(X)+ CП(Y)+ CП(Z,W). (34) В общепринятой форме приведенные затраты представляются в виде: CП =E×CK +CЭ , (35) где E =0,15 – нормативный коэффициент окупаемости для химической промышленности. Будем считать, что капитальные затраты не зависят от структуры системы, и CП(X) определяется только эксплуатационными затратами CЭ(X), связанными с подготовкой технологического оборудования и утилизацией промывных вод при смене ассортимента продукции. При этих допущениях критерий оптимальности может быть представлен в виде CП( + E× + E где x’ijkl = xijklh-1 Ù xijklh. (37) Представление критерия в виде (35) обеспечивает свойство сепарабельности.
Рис. 2. Структура декомпозиционного алгоритма оптимизации многопродуктовых химико-технологических систем: 1 – алгоритм оптимизации аппаратурной структуры химико-технологической системы; 2 – алгоритм оптимизации размеров, производительности и количества единиц стандартного оборудования; 3 – алгоритм оптимизации конструкционных параметров нестандартного оборудования и режимных параметров технологических процессов. ДЕКОМПОЗИЦИОННЫЙ АЛГОРИТМ
Предлагаемый алгоритм имеет трехуровневую структуру (рис. 2). Алгоритм верхнего уровня представляет структурную оптимизацию многопродуктовой системы, состоящую в поиске оптимальных значений структурных параметров X, являющихся булевскими переменными при фиксированных аппаратурном составе и значениях режимных параметров технологического процесса. Задача оптимизации являет собой задачу целочисленного программирования [1]. Средний уровень представляет задачу оптимизации определяющих размеров и производительности стандартного технологического оборудования, формулируемую как задача частично-дискретного программирования. Для ее решения разработан декомпозиционно-эвристический алгоритм с поиском оптимального режима согласования работы технологического оборудования, взаимодействующего через промежуточные емкости [4,6]. На нижнем уровне решается задача оптимизации режимных параметров технологических процессов и их продолжительности в аппаратах периодического действия. Алгоритм состоит в решении задачи Коши для совместных систем обыкновенных дифференциальных и алгебраических уравнений с нулевым индексом [12]. ОБОЗНАЧЕНИЯ в формулах A - множество типов аппаратов, назначаемых конкретному технологическому процессу, a - текущий номер индивидуальной химико-технологической системы, a* - количество индивидуальных химико-технологических систем в составе многопродуктовой химико-технологической системы, b - текущий номер аппарата в составе химико-технологической системы, b* - количество типоразмеров в составе индивидуальной химико-технологической системы, С - затраты, вызванные изменением структуры системы, C*- цена стандартного технологического аппарата, C’ - цена демпфирующей емкости, Ск - капитальные затраты, Сэ - эксплуатационные затраты, Сn - приведенные затраты, c - концентрация компонента химической реакции, D - множество размеров аппаратов, принадлежащих конкретному параметрическому ряду, E - множество стадий получения конкретного продукта, F - известные функции, F* - количество режимных параметров технологического процесса, f*- количество технологических операций, образующих стадию технологического процесса, G - производительность системы по продукту, g - массовый размер порции продукта, DH - тепловой эффект химической реакции, h - номер итерации, I - количество продуктов, I’- количество компонентов химической реакции, i - текущий номер продукта, J - количество технологических стадий, j - текущий номер технологической стадии, K - количество групп (серий) продуктов, k - текущий номер группы (серии) продуктов, l - текущий номер аппарата в параметрическом ряду, M - молекулярная масса компонента, N - количество единиц cтандартного оборудования, N’- количество единиц неcтандартного оборудования, n - количество порций продукта, O - технологическая операция, P - количество единиц оборудования в аппаратурном блоке, p - текущий номер аппаратурного блока, Q - количество аппаратурных блоков, Q* - количество конструкционных параметров нестандартного аппарата, q - текущий номер физико-химического процесса в составе технологической операции, q* - количество физико-химических процессов, составляющих технологическую операцию, r - скорость химической реакции, S - обозначение системы, s - материальный индекс, T - абсолютная температура, T’- температура теплоносителя или хладагента, T0 - фонд времени, t - время, U - объем демпфирующей емкости, u - объем реакционной массы в демпфирующей емкости, V - определяющий размер аппарата периодического действия, v - объем реакционной массы, содержащейся в аппарате периодического действия, W - массив режимных параметров технологических процессов, w - режимный параметр технологического процесса, X - массив структурных параметров, x = 0; 1 - структурный параметр (булевская переменная), Y - массив размеров стандартного технологического оборудования, y - определяющий размер стандартного технологического аппарата, Z - массив конструкционных параметров нестандартного оборудования, z - конструкционный параметр нестандартного оборудования, a - коэффициент в выражении критерия оптимальности, b - показатель степени в выражении критерия оптимальности, g - коэффициент в выражении критерия оптимальности, d - показатель степени в выражении критерия оптимальности, q - продолжительность технологического цикла подсистемы аппаратов, взаимодействующих через демпфирующую емкость, e - уравнения физико-химического процесса, c - координирующая модель, m - модель системы или ее подсистемы, p - натуральные числа, t - продолжительность технологического цикла, tL - продолжительность лимитирующей стадии процесса, Dt - интервал времени между моментами начала первой загрузки и разгрузки демпфирующей емкости, НОК (x1,x2,...,xn) - наименьшее общее кратное целых чисел (x1,x2,...,xn) , ½½- мощность множества, Ú - дизъюнкция в двузначной логике, Ç - пересечение множеств. Список литературы 1. Алексеев О.Г. Комплексное применение методов дискретной оптимизации. - М.: Наука, 1987.-248 с. 2. Лапидус А.Г. Экономическая оптимизация химических производств. - М.: Химия, 1986.- 208с. 3. Лэсдон Л.С. Оптимизация больших систем. - М.: Наука, 1975.- 432 с. 4. Макаров В.В. // Теоретические основы химической технологии. - т. 28.- № 5. - с. 453-464. 5. Первозванский А.А., Гайцгори В.Г. Декомпозиция, агрегирование и приближенная оптимизация.- М.: Наука, 1979.- 344 с. 6. Сбоева Ю.В., Макаров В.В., Круглик А.Е. Деп. в ВИНИТИ 13.10.93, № 2579, 10 с. 7. Цурков В.И. Декомпозиция в задачах большой размерности.- М.: Наука, 1981.-352 с. 8. Duran M.A., Grossman I.E. Math. Prog., 1986, V.96. p.307-339. 9. Floudas C.A., Aggarwal A., Ciric A.R. Comput. Chem. Eng., 1989, V.13. p.1117-1132. 10. Geoffrion A.M. Optim Theory Appl., 1972, V.10. p.237-260. 11. Kocis G.R., Grossman I.E. Ind. Eng. Chem. Res., 1987, V.96. p.1869-1880. 12. Pantelides C.C., Gritsis D., Morison K.R., Sargent R.W.H. Comp. Chem. Eng., 1988, V 12. p.449-454. 13. Papageorgaki S., Reklaitis G.V. Ind. Eng. Chem. Res., 1990, V 29. Р.2054-2062. 14. Papageorgaki S., Reklaitis G.V., Ind. Eng. Chem. Res., 1990, V 29.Р.2062-2073. |
http://swsys.ru/index.php?id=1014&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Оптимизация обработки информационных запросов в СУБД
- Методы восстановления пропусков в массивах данных
- Гибридная экспертная система проектирования ресурсосберегающих установок первичной нефтепереработки
- Системы баз данных и знаний, разработанные в Республике Куба

 в течение заданного интервала времени, например года T0. Пусть для этого имеется набор технологического оборудования, объединенного в параметрические ряды. Оборудование определенных размеров или производительности образует его тип, при этом оборудование каждого типа может быть представлено несколькими единицами. Заданы возможные технологические маршруты каждого продукта, предусматривающие последовательность технологических стадий, типы технологического оборудования для каждой стадии, а также продолжительность технологических операций и, следовательно, технологических стадий, которые будем считать функциями массового размера или объема порции продукта и типа применяемого оборудования. Пусть задан способ материального взаимодействия технологических аппаратов (непосредственно или через демпфирующие накопители), продолжительность их подготовки при изменении ассортимента продуктов. В качестве критерия оптимальности примем приведенные затраты. Допустим, что технологическое оборудование, оформляющее стадии технологического процесса, может объединяться в группы, в которые могут входить аппараты разных размеров, принадлежащие к одному параметрическому ряду и функционирующие как синхронно, так и со смещением во времени. В состав химико-технологических систем может при необходимости входить проектируемое нестандартное технологическое оборудование. Требуется найти оптимальные значения структурных параметров (количество одинаковых аппаратов в группе, количество групп, оформляющих стадии технологического процесса), размеры аппаратов периодического действия и объемы демпфирующих емкостей, производительность аппаратов полунепрерывного действия, продолжительность технологических операций, стадий производства отдельных групп продуктов, конструкционных параметров нестандартного технологического оборудования и режимных параметров технологических процессов.
в течение заданного интервала времени, например года T0. Пусть для этого имеется набор технологического оборудования, объединенного в параметрические ряды. Оборудование определенных размеров или производительности образует его тип, при этом оборудование каждого типа может быть представлено несколькими единицами. Заданы возможные технологические маршруты каждого продукта, предусматривающие последовательность технологических стадий, типы технологического оборудования для каждой стадии, а также продолжительность технологических операций и, следовательно, технологических стадий, которые будем считать функциями массового размера или объема порции продукта и типа применяемого оборудования. Пусть задан способ материального взаимодействия технологических аппаратов (непосредственно или через демпфирующие накопители), продолжительность их подготовки при изменении ассортимента продуктов. В качестве критерия оптимальности примем приведенные затраты. Допустим, что технологическое оборудование, оформляющее стадии технологического процесса, может объединяться в группы, в которые могут входить аппараты разных размеров, принадлежащие к одному параметрическому ряду и функционирующие как синхронно, так и со смещением во времени. В состав химико-технологических систем может при необходимости входить проектируемое нестандартное технологическое оборудование. Требуется найти оптимальные значения структурных параметров (количество одинаковых аппаратов в группе, количество групп, оформляющих стадии технологического процесса), размеры аппаратов периодического действия и объемы демпфирующих емкостей, производительность аппаратов полунепрерывного действия, продолжительность технологических операций, стадий производства отдельных групп продуктов, конструкционных параметров нестандартного технологического оборудования и режимных параметров технологических процессов.
 - модель a-той индивидуальной химико-технологической системы;
- модель a-той индивидуальной химико-технологической системы; - модель b-го технологического аппарата в составе a-той индивидуальной химико-технологической системы;
- модель b-го технологического аппарата в составе a-той индивидуальной химико-технологической системы; - модель f-той технологической операции в b-том аппарате в составе a-той системы;
- модель f-той технологической операции в b-том аппарате в составе a-той системы; - система уравнений математического описания q-го физико-химического процесса в составе f-той технологической операции в b-том аппарате в составе a-той системы;
- система уравнений математического описания q-го физико-химического процесса в составе f-той технологической операции в b-том аппарате в составе a-той системы; (2)
(2) (3)
(3) .
. ; p=
; p= ;
; jÎ Ei ;k=
jÎ Ei ;k= nij × gik ³ Gi ; i=
nij × gik ³ Gi ; i= ; i=
; i= ; (12)
; (12) xijkl ; i=
xijkl ; i= Vle ; lÎAij ; eÎ Df , (16)
Vle ; lÎAij ; eÎ Df , (16) pi ; lÎ Aij , (17)
pi ; lÎ Aij , (17) pi; i=
pi; i= £ Vjl £
£ Vjl £ ; (21)
; (21)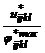 £ Ujl £
£ Ujl £  ; (22)
; (22) {uijkl (t, Dtijkl )}; (23)
{uijkl (t, Dtijkl )}; (23) (28)
(28) ; Tijkl(0)=T’ijkl , (29)
; Tijkl(0)=T’ijkl , (29)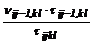 , (32)
, (32) , i=
, i= Cijkl × x’ijkl +
Cijkl × x’ijkl + Nj × Cj* × (
Nj × Cj* × ( ) + C’j(
) + C’j( ) +
) + Nj × gj ×
Nj × gj × , (36)
, (36)