Получение асимптотических разложений термодинамических функций методами компьютерной алгебры
| Николаев А.В. (elodssa@yandex.ru) - Чайковский технологический институт, кандидат технических наук, Вшивцев А.С. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Рассмотрены возможности приложения современных систем компьютерной алгебры для аналитического вычисления термодинамических функций в рамках теории возмущений. В качестве примера подробно изложена процедура получения высокотемпературных асимптотических разложений термодинамического потенциала идеального бозе-газа во внешнем магнитном поле в системе Mathematica версии 3.0. Как известно, в теоретической физике весьма ограниченный класс задач имеют точные аналитические решения, а большинство реалистичных моделей с трудом поддаются исследованию в точном виде. Существует два основных общепринятых подхода к изучению подобных задач. Один из них основывается на численных оценках с использованием вычислительной техники. К преимуществам этой методики относятся хорошо разработанный математический аппарат и наличие богатого количества широкодоступных эффективных программных библиотек. Основными недостатками численного подхода является трудность в анализе влияния различных параметров модели на ее поведение, и необходимость делать произвольные допущения относительно требуемой точности проводимых расчетов - что, конечно, затрудняет изучение физической сущности рассматриваемой теоретической модели. Другим традиционным подходом к исследованию реалистических моделей является метод теории возмущений, опирающийся на рассмотрение малых поправок к точно решаемым задачам. Эта методика обладает тем неоспоримым преимуществом, что позволяет выявить влияние параметров математической модели на ее поведение и их связь с сущностью физического явления. Основной трудностью подхода является то, что получение поправок уже второго порядка, как правило, приводит к весьма громоздким формулам, при работе с которыми очень легко допустить ошибку. Вычисление поправок более высоких порядков обычно вообще не проводится в виду их исключительной трудоемкости. В связи с этим автоматизация процесса работы с рядами теории возмущений является важной задачей [1]. Компьютерные средства аналитических вычислений, как отдельный класс программного обеспечения (удачное определение понятия “компьютерная алгебра” дано в [2]), появились уже сравнительно давно, еще в 1960-ых годах [3]. Однако в течение долгого времени они были технически несовершенны и имели ограниченную применимость - и поэтому в значительной степени игнорировались научной средой и находились в стороне от основного направления использования вычислительной техники в научных расчетах. (Детальный анализ требований, предъявляемых к практической системе символьных вычислений, приведен в [4]). Причин подобному положению дел было несколько, как технологического, так и экономического характера. Это, прежде всего, неэффективность известных тогда алгоритмов, а также недостаточность выразительности языковых средств для оперирования абстрактными математическими понятиями. Кроме того, большинство программного обеспечения писалось в те годы в расчете на конкретную аппаратную архитектуру, и поэтому возможности широкого распространения имеющихся пакетов были заранее ограничены. Даже такие системы, как Reduce, написанный на языке высокого уровня LISP, были труднопереносимы из-за наличия многочисленных несовместимых реализаций входного языка. Наконец, комплексность алгоритмов символьных операций предъявляет высокие требования к необходимому объему оперативной памяти и быстродействию вычислительной техники - и ввиду ее высокой стоимости пакеты аналитических вычислений были малодоступны для большинства научных работников. Обзор ранних работ по применению компьютерной алгебры содержится в [5], а ссылки на российские работы этого периода приведены в [6]. За последние годы, приблизительно с конца 1980-ых годов, положение резко изменилось. Бурное развитие микропроцессорной технологии, позволившее перейти к разработке переносимого программного обеспечения на языках высокого уровня, при резком снижении цен на вычислительную технику создало широкий рынок для систем символьных вычислений. Это привело к появлению пакетов математических вычислений, реализованных для широкого спектра компьютерной архитектуры - таких как, например, Reduce и Macsyma. В настоящее время на рынке имеется большой выбор средств компьютерной алгебры, как общего характера, так и специализированных: например, в [7] собраны подробные данные о 43 системах символьных вычислений. (Кратое введение в возможности применения в физике содержится в [8]. О приложении компьютерной алгебры для вычисления частных производных термодинамических функций см. [9,10].) Особое место среди компьютерных средств символьных вычислений принадлежит интегрированным системам Maple и Mathematica, получивших повсеместное распространение на рабочих станциях и персональных компьютерах. Эти системы отличаются высокой степенью универсальности, что делает их мощными инструментами для математических расчетов в широком диапазона научных и технических приложений. (Детальное сравнение двух этих систем с точки зрения использования в физике содержится в [11]). По мнению создателя системы Mathematica Стивена Вольфрама [12], причина гибкости и универсальности системы Mathematica заключается в выразительности ее входного языка, в основу которого положено небольшое число исходных понятий высокой степени общности. Повсеместное распространение и стандартизация средств аналитических вычислений уже привело к появлению научных работ (см., например, сборник [13] или [14]) и математических учебников [15], где вместо традиционной математической нотации используются алгоритмические языки конкретных систем аналитических вычислений. По мнению некоторые авторов, современные средства компьютерной алгебры в определенном смысле даже меняют смысл того, что, собственно говоря, и составляет “решение” физической проблемы [16]. (За порцией здорового скептицизма в этом отношении и об опасностях, подстерегающих неосмотрительных и чересчур доверчивых пользователей систем символьных вычислений, можно обратиться к [17]. Там же приведены поучительные примеры того, как понимание математической сути проблемы ведет к формулировке задачи для компьютера в более эффективной форме.) Несмотря на то, что в настоящее время работы, излагающие математическую сторону дела непосредственно на языке системы компьютерной алгебры, имеют узкоспециальный характер и, по-видимому, остаются некоторого рода курьезом, нельзя не обратить внимание на два важных преимущества такого стиля для публикации научных результатов - в частности, в области теоретической физики. Во-первых, алгоритмический язык обладает значительно большей выразительностью для описания математических преобразований, чем естественный "человеческий" язык, и в-отличие от последнего, точен и недвусмысленнен. Во-вторых, при наличии готовой процедуры, написанной на символьном языке и широкой доступности его реализаций на конкретных компьютерах читатель может сразу же повторить оригинальные вычисления - скажем, с большей степенью точности или для конкретного частного случая. Высокая степень абстрактности современных языков символьных вычислений и их близость к общепринятому способу математической записи делают их несравненно более приемлимыми для этой цели, чем, например, процедурные языки типа FORTRANа или С, или классические символьные языки, такие как LISP. Настоящая работа представляет собой нашу попытку публикации такого рода. Основной технической трудностью в использовании асимптотических методов является печально известная “громоздкость” получающихся выражений (не избежала этой участи и данная диссертационная работа). Однако серьезным достоинством описанных выше процедур является возможность естественно сформулировать их на алегбраическом компьютерном языке. В этой главе, в качестве примера, подробно изложена реализация в системе Mathematica 3.0 процедуры получения высокотемпературных асимптотических разложений термодинамического потенциала идеального бозе-газа во внешнем магнитном поле согласно предложенной нами методике [18]. Исследуемая задача, в силу своей трудоемкости, по-видимому, может служить хорошим примером для иллюстрации того, как современные средства автоматической обработки символьной информации позволяют по-новому взглянуть на место и сущность аналитических методов вычислений в аппарате теоретической физики. Энергетический спектр бесспиновой бозе (скалярной) частицы с зарядом, равном заряду электрона e и массой m в постоянном и однородном магнитном поле напряженностью H имеет следующий вид [19]: energy[m_, eH_][p_,n_] = Sqrt[m^2 + p^2 + eH(2n+1)]
и, следовательно, его термодинамический терминал W будет равен [20]: omega = eH/(4Pi^2 beta)* Log[1-Exp[beta(mu - energy[m,eH][p,n])]]
где b - это обратная температура, p - проекция импульса частицы на направление магнитного поля, а m - химический потенциал. В формуле подразумевается интегрирование в бесконечных пределах по p и суммирование по n от 0 до ¥, которые мы не стали выписывать явно во избежание громоздких формул - а просто "запомнили". Это мы будем делать и далее при работе с суммами и интегралами. Займемся приведением выражения для термодинамического потенциала к виду, удобному для получения асимптотических разложений. Прежде всего, разложим в ряд логарифмическую функцию и упростим внешний вид получившегося представления: omega = omega /. logSeries[k] /. (-x_)^n_:1 :> (-1)^n x^n /. (-1)^((2n_:1) + m_) :> (-1)^m /. Exp[x_]^k_ :> Exp[Distribute[k x]]
В приведенной выше последовательности преобразований мы объединили вместе несколько следующих друг за другом операций и пропустили промежуточные результаты, печатаемые Mathematic'ой. Так мы будем поступать и в дальнейшем в целях экономии места. Мы также воспользовались функцией logSeries[], определение которой, как и определения других вспомогательных функций, приведено в Приложении. Интеграл по проекции импульса частицы теперь можно вычислить точно. Отметим, что Mathematica не умеет самостоятельно брать гауссовы интегралы, и поэтому приходится обращаться к таблицам. (Здесь можно заметить, что судя по всему, С.Вольфрам все же поспешил с заявлением [21], что Mathematica уже превзошла способности человека в вычислении интегралов). Итак, воспользовавшись определенной нами функцией gauss[], получим: omega = omega /. Exp[a_ + x:(-b_ Sqrt[_])] :> Exp[a] (Exp[x] /. gauss[p])
Перейдем теперь к суммированию по n (по уровням Ландау). Прежде всего, чтобы избавиться от радикала, воспользуемся свойствами функций Макдональда, и представим функцию K1(z) в виде производной по b. Чтобы не дать Mathematic'е сразу же взять производную, заключим оператор дифференцирования D внутрь HoldForm[]: omega = omega /. z_ BesselK[1,beta k z_] :> -1/k HoldForm[D][BesselK[0,beta k z],beta]
Воспользовавшись интегральным представлением Зоммерфельда для функций Макдональда [22]: omega = omega /. sommerfeld[t]
где по t подразумевается интегрирование от 0 до ¥, возьмем сумму по уровням Ландау под знаком дифференцирования, после преобразования внешнего вида получим: omega = omega /. HoldForm[D][x_,y_] :> HoldForm[D][Sum[x,n,0,Infinity],y] //. (x_^y_)^z_ :> x^(y z) /. 1/x:(1-Exp[_]) :> -1/(-x) /. 1/(Exp[x_]-1) :> Exp[-x/2]/(2 Sinh[x/2])
Чтобы упростить вид последней формулы, сделаем замену переменных под знаком интеграла с помощью написанной нами функции substVar[] - таким образом, чтобы в аргументе гиперболического косеканса стояла просто переменная t. После этого, сняв HoldForm[] с оператора дифференцирования, продифференцируем по обратной температуре b, и придем к выражению, удобному для вычисления асимптотик: omega = omega /. HoldForm[D][x_,y_] :> HoldForm[D][substVar[x, Cases[x, Csch[z_] | Coth[z_] :> z][[1]] == t1, t -> t1], y] /. t1 -> t // ReleaseHold
Перейдем к получению разложения W в пределе высоких температур и сверхсильных магнитных полей, которое будем проводить по трем безразмерным параметрам c<<1, r<<1, g>>1 (таким образом, в изучаемом пределе "температура сильнее поля"): omega = omega /. Solve[chi == beta Sqrt[eH], beta][[1]] /. Solve[ro == mu/Sqrt[eH], mu][[1]] /. Solve[gamma == eH/m^2, eH][[1]]
Разложив экспоненту в ряд по малому параметру 1/g и перегруппировав сомножители, получим: omega = omega /. Exp[x_ + y:(-t/gamma)] :> Exp[x] (Exp[y] /. expSeries[n]) /. x:(_^_) :> Distribute[x,Times] /. (1/x_)^n_. :> x^(-n)
где подразумевается суммирование по n от 0 до ¥ (не забудем также про суммирование по k и интегрирование по t). Введя величину An(c,r), значение которой временно для краткости в записи последующих операций обозначим как aN: aN = Times @@ Cases[omega, x_ /; Not[FreeQ[x,chi] && FreeQ[x,t]]] /. n -> n+1
перепишем термодинамический потенциал W в виде степенного ряда по параметру напряженности поля, с коэффициентами, зависящими от двух других параметров: omega = HoldForm[Sum][replaceProduct[omega, (aN /. n -> n-1) :> HoldForm[a][n-1][chi,ro]], {n,0,1}]
Как видно из приведенной формулы, в сумме по n мы удержали только два первых члена ряда - и, таким образом, ограничились точностью до первого порядка по g. Что же касается технической стороны дела, то мы прибегли к функции HoldForm[], чтобы не дать Mathematic'е выписать сумму почленно. Мы также использовали нашу собственную функцию replaceProduct[] для замены произведения нескольких слагаемых по заданному образцу, поскольку встроенная функция Replace[] не всегда справляется с этим. Займемся нахождением асимптотического разложения коэффициентов полученного ряда по c и r. Разложение по r получается сразу же подстановкой ряда Тейлора вместо экспоненты: aN = aN /. Exp[x_ + y_] /; FreeQ[y,ro] -> (Exp[x] /. expSeries[j]) Exp[y] // expandPower
(Использованная здесь функция expandPower[] возводит в степень и упрощает произведения нескольких сомножителей.) Таким образом, величины An(c,r) выразятся в виде степенного ряда по r, с коэффициентами Anj(c), зависящими от c: aNJ = aN j!/ro^j; a[n_ ? NumberQ][chi_,ro_] = HoldForm[Sum][ deleteProduct[aN,aNJ] HoldForm[a][n,j][chi], {j,0,1}]
где мы ограничились линейными по r членами ряда, а Anj(c) определено как aNJ
Для вычисления асимптотик Anj(c) по параметру c сделаем преобразование Меллина по этой величине, возьмем интеграл по t от полученного образа, а затем произведем обратное преобразование Меллина и вычислим контурный интеграл по теории вычетов. Это легче сделать, предварительно произведя замену переменной: aNJ = substVar[aNJ, t == k chi t1, t -> t1] /. t1 -> t // expandPower
Mathematica почему-то не может непосредственно вычислить образ Меллина от последнего выражения, но тем не менее находит значение соответствующего табличного интеграла. Поэтому приходится идти обходным путем. Взяв интеграл в общем виде: integral = (# -> Integrate[#,t,0,Infinity][[2]])&[ Exp[p t] t^n Csch[c t]]
изготовив из него параметризованное правило для замены по образцу с помощью вспомогательной функции createRule[], произведя замену, и наконец, сняв суммирование по k, придем к следующему представлению Anj(c) в виде неявно подразумеваемого контурного интеграла: aNJ = chi^(-s) replaceProduct[aNJ chi^(s-1), createRule[integral /. t -> chi,p,n,c]] /. Zeta[x_,y_] :> Zeta[x,Expand[Simplify[y]]] // expandPower // Sum[#,k,1,Infinity]&
Вычислять интеграл по t от последнего выражения Mathematica также не умеет, и поэтому необходимо обращаться к таблицам. Сделав замену: aNJ = -substVar[aNJ, t == 1/Sqrt[t1], t -> t1] /. t1 -> t // expandPower
(отметим, что появление знака минус обусловлено перестановкой верхнего и нижнего предела интегрирования), подставив значение интеграла из таблиц [23], и воспользовавшись определением бета-функции, придем к следующему выражению: aNJ = Simplify[aNJ /. createRule[ t^(a-1) Zeta[s,c_. + d t] -> d^(-a) Beta[a,s-a] Zeta[s-a,c] /. a -> a+1, {a,d,s}]] /. Beta[x_,y_] :> Gamma[x] Gamma[y]/Gamma[Simplify[x+y]]
Вычислив контурный интеграл в последнем выражении с точностью до слагаемых, пророциональных c-3, получим асимптотическое разложение величин Anj(c): a[n_ ? NumberQ, j_ ? NumberQ][chi_] = HoldForm[asymptotic][aNJ, s, Cases[aNJ, chi^x_ :> Solve[x == 3, s]][[1,1,1,2]] ]
Здесь мы воспользовались написанной нами функцией asymptotic[], которая, анализируя полюсную структуру выражения, находит особые точках, лежащие на вещественной оси правее заданного предела точности, и вычисляет сумму вычетов на этом множестве точек. Итак, мы пришли к асимптотическому разложению термодинамического потенциала с выбранной нами степенью точности. Сняв три уровня скобок HoldForm[], выпишем результат в явном виде: Nest[ReleaseHold, omega, 3]
Для наглядности приведем также W в виде суммы: ReleaseHold[omega] /. HoldForm[Sum] -> Sum
и асимптотики величин Anj(c), входящий в нее: a[-1,0][chi] // ReleaseHold
a[-1,1][chi] // ReleaseHold
a[0,0][chi] // ReleaseHold
a[0,1][chi] // ReleaseHold
Описанная процедура пригодна для получения асимптотик с любой заданной точностью - конечно, до тех пор, пока объем вычислений не привысит возможности конкретного компьютера. Единственное, что необходимо для этого сделать - это изменить верхние пределы в выписанных нами суммах. Наши расчеты проводились в системе Mathematica 3.0 на персональном компьютере с процессором Pentium Pro частотой 200 MHz, с 64 Мб оперативной памяти, в операционной системе Windows NT 4.0. На все приведенные выше вычисления ушло 40,617 сек чистого времени, подсчитанного с помощью встроенной функции TimeUsed[], из которого на вычисление асимптотического разложения в (22) ушло 17,825 сек. Сходным образом выкладки можно провести и с предыдущей версией системы, Mathematica 2.2, однако новейшая версия имеет для нашей задачи несколько преимуществ. Это во-первых, более мощный блок интегрирования (который, как мы видели, все же не всегда справляется с табличными интегралами). Во-вторых, встроенная в новую версию ядра система аналитического вычисления сумм, пришедшая на смену стандартному пакету SymbolicSum, вычисляет суммы, приводящиеся к дзета-функциям, для оперирования которыми прежде приходилось пускаться на всевозможные ухищрения. Таким образом, мы видим, что средства компьютерной алгебры, и в частости, система Mathematica, являются весьма эффективным средством нахождения асимптотических разложений термодинамических функций. Основными достоинствами подобных систем для этого рода задач является возможность безошибочного оперирования громоздкими формулами и способность находить вычеты в особых точках при вычислении контурного интеграла обратного образа Меллина. Среди недостатков же аналитического ядра конкретной системы Mathematica (в ее последней версии 3.0) пока можно назвать невозможность прямого вычисления некоторых классов определенных интегралов, в особенности, содержащих специальные функции - например, гипергеометрические и дзета-функции Римана. (Несмотря на утверждения создателей Mathematic'и, авторы пришли к заключению, что время расстаться со старыми видавшими виды таблицами сумм и интегралов пока еще не пришло.) Неудобством является также отсутствие встроенной возможности производить выборочную подстановку по образцу в произведениях. Разумеется, представленный алгоритм немедленно переписывается в виде подгружаемого в среду Mathematica стандартного пакета. Однако в настоящей работе мы не стали этого делать по двум причинам. Во-первых, мы намеренно попытались приблизить стиль изложения к общепринятому в физико-математической литературе. Нам было интересно попробовать использовать формальный компьютерный язык для изложения проводимых преобразований вместо традиционного сочетания математических формул и словестных пояснений - причем не для описания реализации математической процедуры на компьютере, а для описания самой процедуры. Иными словами, нам хотелось посмотреть, как с помощью компьютерной алгебры можно в принципе по-иному подходить к изложению и публикации физических результатов. Во-вторых, при таком подходе можно проследить за получаемыми на каждом шагу результатами, и оценить, насколько хорошо данная конкретная система символьных вычислений справляется с делом. Как мы видели, Mathematica не всегда оказывается на высоте положения, и приходится пользоваться “подручными” средствами. Такие наблюдения естественно производить в диалоговом режиме. Итак, в результате значительного совершенствования средств компьютерной алгебры становится актуальным вопрос о месте, занимаемым асимптотическими методами в аппарате теоретической физики. Можно высказать предположение, что наряду с исследованиями поведения "возмущенных" систем в низших порядках приближения, получение высоких порядков асимптотических разложений с помощью компьютера позволит для определенных классов задач добиться степени точности, достаточной для количественных оценок. Список литературы 1. A.Hsieh, E.Yehudai, HIP: Symbolic high-energy physics calculations, Comp. Phys., v. 6, No 3, pp.253-261, 1992. 2. D.Hartley, Overview of computer algebra in relativity, in F.W.Hehl et al., ed., Relativity and scientific computing. Computer algebra, numerics, visualization, Springer, 1996. 3. J.H.Davenport, Y.Siret, E.Tournier, Computer algebra. Systems and algorithms for algebraic computation, 2nd Ed., Academic Press, 1993. 4. G.J.A.Schneider, Computer algebra systems. How do they change mathematics?, in J. Fleischer et al., ed., Computer algebra in science and engineering : 28-31 August 1994, Bielefeld, Germany, World Scientific, 1995. 5. H.I.Cohen, J.P.Fitch, Uses made of computer algebra in physics, J. Symbolic Comp., v. 11, pp. 291-305, 1991. 6. N.M.Glazunov, F.G.Karpinskii, V.V.Kornyak, Solving some problems of algebra, analysis, and mathematical physics using computer algebra systems, Cybernetics, v. 27, No 2, pp.189-198, 1991. (На русском языке статья опубликована в журн. Кибернетика, ¹ 2, с. 23-29, 1991). 7. S.M.Christensen, Resources for Computer Algebra, v. 8, No 3, pp.308-316, 1994. 8. D.Waxman, Impact of computer algebra in physics, Cont. Phys., v. 36, No 5, pp. 321-327, 1995. 9. N.Farah, R.W.Missen, The computer-derivation of thermodynamic equations. Part I: First and second derivatives for simple systems, Canadian Journ. Chem. Eng., v. 64, pp. 154-157, 1986. 10. N.Farah, R.W.Missen, The computer-derivation of thermodynamic equations. Part II: First and second derivatives for complex systems, Canadian Journ. Chem. Eng., v. 65, pp. 137-141, 1987. 11. W.J.Thompson, Mathematica and Maple: has Champaign met its Waterloo?, Comp. Phys., v.8, No 3, pp.269-278, 1994. 12. S. Wolfram, The Mathematica book, 3rd Ed., Wolfram Media/Cambridge University Press, 1996. 13. J. Fleischer et al., ed., Computer algebra in science and engineering : 28-31 August 1994, Bielefeld, Germany, World Scientific, 1995. 14. D.Dill, Implementing matrix mechanics in Mathematica: Determination of Clebsch-Gordan coefficients by matrix diagonalization, Comp. Phys., pp. 616-624, 1991. 15. A.Gray, Modern differential geometry of curves and surfaces, CRC Press, 1993. 16. R.E.Crandall, Symbolic software supports new adventures in physics, Comp. Phys., v. 5, No 6, pp. 576-624, 1991. 17. J.M.Aguirregabiria, A.Hernandez, Are we careful enough when using computer algebra?, Comp. Phys., v. 8, No 1, pp. 56-61, 1994. 18. А.С.Вшивцев, А.В.Николаев, В.Р.Халилов, Термодинамика скалярных и ферми- частиц в сильном магнитном поле, Ред. ж. "Известия вузов, Физика", Томск, 1990, Деп. в ВИНИТИ, рег. ¹ 3329-В90 от 16 июня 1990. 19. Wu-yang Tsai, Energy eigenvalues for charged particles in a homogeneous magnetic field - an application of the Foldy-Wouthuysen transformation, Phys. Rev., v. 7, No 6, pp.1945-1948, 1973. 20. Л.Д.Ландау, Е.М.Лифшиц, Статистическая физика, ч.1, М., 1995. 21. S.Wolfram, The vision of Mathematica, lecture at Columbia University, October 1, 1996, New York. 22. А.Ф.Никифоров, В.Б.Уваров, Специальные функции математической физики, Наука, 1984. 23. А.П.Прудников, Ю.А.Брычков, О.И.Маричев, Интегралы и ряды. Дополнительные главы. М., Наука, 1986. |
http://swsys.ru/index.php?id=1030&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Анализ российского и зарубежного рынков программных продуктов
- Интерактивная процедура построения модели тренда для экономических показателей
- Комплекс программных средств для аналитических иерархических процессов экспертного оценивания
- Потоковый анализ программ, управляемый знаниями

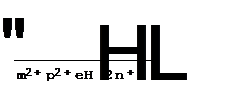 , (1)
, (1) , (2)
, (2)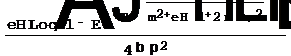 . (3)
. (3)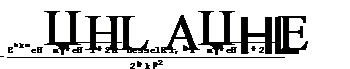 . (4)
. (4) . (5)
. (5)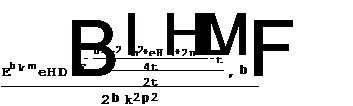 , (6)
, (6) . (7)
. (7) . (8)
. (8)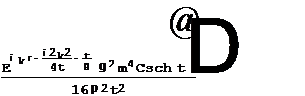 . (9)
. (9) , (10)
, (10) , (11)
, (11) . (12)
. (12) . (13)
. (13)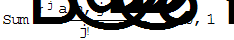 , (14)
, (14)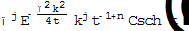 . (15)
. (15)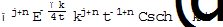 (16)
(16) , (17)
, (17) . (18)
. (18) , (19)
, (19) . (20)
. (20) . (21)
. (21) (22)
(22) , (23)
, (23) , (24)
, (24) , (25)
, (25) , (26)
, (26) . (27)
. (27)