Два алгоритма определения множества парето-оптимальных решений многокритериальной задачи линейного программирования
| Смирнов Д.В. () - , Берзин E.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
При проектировании, разработке и оценке качества любых сложных систем, к которым также относятся и системы программных продуктов, возникает необходимость выполнения системы весьма противоречивых требований. Если эти требования к системе удается выразить в виде некоторой совокупности частных количественных показателей (частных критериев – ч-критериев), то задача проектирования может быть формализована в виде многокритериальной векторной задачи математического программирования (ВЗМП):
где (1) означает, что увеличение любого из r ч-критериев улучшает качество системы;[1] X=(xj)n – (решение ЛПР) параметры, управляемые лицом, принимающим решение (ЛПР); Dx – область допустимых решений ЛПР. Далее будем считать, что ч-критерии линейны, а область замкнута и ограничена линейными неравенствами. Тогда многокритериальная (векторная) задача ЛП (ВЗЛП) запишется в виде:
где в записи справа ограничения представлены в виде неотрицательных линейных функций (переменных) ВЗЛП (3), (4) не является оптимизационной задачей, так как говорить об оптимальности решения можно только в смысле одного какого-то ч-критерия из их совокупности (3). Применительно ко всей совокупности (3) можно говорить лишь о некотором рациональном, в большей или меньшей степени практически приемлемом, компромиссном решении, при котором, возможно, ни один из r ч-критериев не примет максимальное значение. Предлагаются различные процедуры для поиска рациональных решений [1-8], однако необходимым условием для каждого такого решения является невозможность его улучшения хотя бы по одному ч-критерию, чтобы при этом ни один из оставшихся не ухудшил своего значения. Такое "неулучшаемое" решение принято называть оптимальным по Парето [1-3], или сокращенно П-оптимальным. Таким образом, решение любой многокритериальной задачи или начинается с поиска всего множества П-оптимальных решений (П-множества), где должно находиться и окончательное, компромиссное решение, или заканчивается проверкой предварительно полученного решения на П-оптимальность и, если потребуется, его последующим улучшением по каким-то ч-критериям без ухудшения значений остальных. Основной целью данной работы является формулировка достаточно простого и легко формализуемого алгоритма, позволяющего определить: – все множество Парето-оптимальных решений ВЗЛП (Dpx); – является ли решение X¢ П-оптимальным и, если потребуется, найти ближайшее к нему П-решение. В основу предлагаемого метода положено формальное условие П-оптимальности решения X¢[1;2]: решение X¢ÎDx П-оптимально, если не существует такого другого решения XÎDx, при котором бы выполнялись условия: "k: Lk(X)³Lk(X¢), т.е.Dk=Lk(X)-Lk(X¢)³0, (5) при этом хотя бы одно из них – строго (Dk1>0). Для формулировки алгоритма условия (5) удобно представить в виде задачи ЛП (ЗЛП):
Условия (7) в геометрическом смысле – это некоторая область, образованная пересечением r n-мерных полупространств, заданных неравенствами (7). В случае совместимости система (7) образует некоторое пространство – конус с вершиной X¢. Каждая точка этого конуса является улучшенным, по сравнению с X¢, решением (в дальнейшем этот конус именуется конусом доминирования, д-конусом). К определению p-множества На рисунке часть этого конуса, расположенная в области Dx, показана отрезком X¢, Xp для следующей ВЗЛП: L1(X)=x1+x2, e1=-5x1+7x2+8, L2(X)=-x1+x2+10, ® max e2=-x1-4x2+34, Dx L3(X)=-x1-x2+16, X e3=2x1-x2-5, L4(X)=-2x1-x2+30, (8) "i,j: xj,ei³0. (9) Примечание Вырожденность д-конуса обусловлена полной противоположностью ч-критериев L1 и L3 – их вектор-градиенты отличаются только знаками. Физически такой случай не может иметь места, т.к. если, например, L1 требует максимизации надежности системы, то L3 – минимизации той же надежности. Однако формальное рассмотрение такой системы ч-критериев не теряет смысла. Смещая точку X¢ внутрь д-конуса, получим улучшенное решение. Такое улучшение (в данном случае по ч-критерию L2) возможно вплоть до смещения в точку Xp, когда весь д-конус, кроме его вершины, окажется вне области Dx. Поскольку выбор точки X¢ никак не влияет на форму и ориентацию д-конуса (соответствует его параллельному переносу в n-мерном октанте), то можно, выбирая X¢ в различных точках Dx, заметить, что все П-множство составят точки, расположенные на ребрах (гранях) АВ и ВС рисунка. Таким образом, из решения ЗЛП (6), (7) при любом выборе вершины д-конуса X¢ в положительном октанте[3] следуют выводы: если Dmax>0, то д-конус существует, а П-множество составят некоторые грани множества Dx; если Dmax=0, то система (7) совместима только в точке X¢, а значит, любая точка X¢ÎDx П-оптимальна (Dpx=Dx). В случае Dmax>0 точка X¢ должна последовательно выбираться на каждой из граней области Dx. Это равносильно добавлению к системе (7) еще одного неравенства, соответствующего i-ой грани (ei³0). Если в ходе решения ЗЛП критерий D(6) увеличится, то данная грань не является П-оптимальной, а если Dmax=0 – грань войдет в множество Dpx. Проверив все m граней симплекса Dx, найдем П-множество Dpx. Перенос множества (6) на грани Dx связан с дополнительными расчетами, поэтому вершину X¢ д-конуса целесообразно выбрать в фиксированной точке X¢=(1)[4] и в эту же точку переносить грани симплекса Dx. Тогда, опуская элементарные преобразования, приведенную к точке X¢=(1)n ЗЛП (6), (7) запишем в виде:
Преобразованные грани симплекса при этом запишутся:
Проиллюстрируем процесс решения на примере (8), (9). Согласно (10)–(11) запишем ЗЛП в систему (12) в алгебраическом и табличном виде T1: T1 x1 x2 1 T2 x1 D1 1 T3 e2 D1 1
D1=x1+x2-2, D1 1 1 -2 x2 -1 1 2 x2 1 D2=-x1+x2, D2 -1 1 0 D2 -2 1 2 D2 0 D3=-x1-x2+2, D3 -1 -1 2 D3 0 -1 0 D3 0(13) D4=-2x1-x2+3, D4 -2 -1 3 D4 -1 -1 1 D4 0 e1=-5x1+7x2-2, e1 -5 7 -2 e1 -12 7 12 e1 0
e3=2x1-x2-1. e3 2 -1 -1 e3 3 -1 -3 e3 0 Методом последовательного улучшения планов [6;7] решается ЗЛП, отчеркнутая в T1 двойной линией. Ограничения ei, записанные под двойной линией просто пересчитываются по формулам обыкновенных жордановых исключений (ОЖИ). После шага ОЖИ (замена D1«x2, T1) получено оптимальное решение. Так как Dmax¹0 (Dmax>0), то д-конус существует и, следовательно, p-множество составят некоторые грани области Dх. Эти грани {eip} определяется путем исключения тех граней, которые не могут войти в Dх. Для них при D>0 имеем ei³0 (грань e1). Номера i оставшихся граней образуют множество I-={i½ei<0,"i}. Последовательная проверка граней iÎI- выявляет грани epi. Так, например, добавив к системе (11) грань e2<0, после шага ОЖИ (e2«х1,Т2) получим решение X0=(1;1) и Dmax=0, из чего следует p-оптимальность грани e2 области Dх. То же для e3 (см.рис.). Чтобы Dpх уберечь от ложных решений, из системы (4) должны быть исключены грани, не образующие границ области Dх. Для этого последовательно "ei³0 заменяется границей ei=0. Если при этом система (4) становится несовместимой, то неравенство ei³0 исключается. Исключаются и линейно зависимые неравенства (см. рис., e4, e5)[5]. Полагая, что такой отсев выполнен, запишем порядок решения задачи. Алгоритм 1 определения p-множества 10. Читать ||aij||, ||ckj| 20. Решить ЗЛП (10), (11), попутно пересчитывая (12) 30. Если Dmax=0, писать Dpх=Dх, идти к 110 40. Исключить из (12) ограничения ei³0, записать (уточнить) множество I--={i | ei<0,"i} 50. Если I-=0, идти к (100) 60. Включить грань ei, iÎI- в систему (11) и решить ЗЛП (10), (II) + ei 70. Если Dmax¹0, i исключить из I-, идти к 40 80. Включить грань ei в Dpх (ei=epi), i исключить из I- 90. Если I-¹0, идти к 60 100. Писать Dpх={epi} 110. Конец Если Dpх найдено, то вопрос о принадлежности ему некоторой произвольной точки Х¢ сводится к подстановке ее компонент х¢j в (9) и вычислению невязок ei. Если при неотрицательности всех невязок хотя бы одна из них, соответствующих П-множеству, равна нулю, то Х¢ÎDpх. Однако для проверки П-оптимальности Х¢ нет необходимости строить все П-множество. Достаточно решить ЗЛП (6), (7), (4). Если Dmax=0 - точка Х¢ П-оптимальна. При Dmax¹0 будет найдено улучшенное решение (см. рис., Х¢ и Хp). В [8] показано, что П-множество ВЗЛП может быть найдено как множество решений ЗЛП при ограничениях (4) и с целевой функцией, полученной как линейная комбинация ч-критериев:[6]
при всевозможных значениях весовых коэффициентов ч-критериев – ak. Недостаток такого подхода заключается в том, что могут быть обнаружены только П-решения, лежащие на границах области Dх. В [2] для случая Dpх=Dх предлагается выбор такого вектора коэффициентов ao=(ak), который все коэффициенты cj в "свертке" (14) обращает в нуль. Такой подход может ввести ложные П-решения. Например, взяв ao=(0,5; 0; 0,5; 0) для системы (8), следовало бы сделать вывод, что Dpх=Dх, но из рисунка видно, что это не так. Укажем вычислительную процедуру, реализующую принцип "свертки" и позволяющую устранить отмеченный недостаток. Суть метода состоит в том, что для обнаружения П-решений, расположенных на i-ой грани (4), необходимо путем выбора вектора ai выполнить два условия: коэффициенты cj (14) и aij i-ой грани должны быть пропорциональны при каждом j; эти коэффициенты должны иметь разные знаки, что обеспечит экстремальное значение "свертки" на i-ой (i=1;m) грани. Полагая коэффициент пропорциональности hi положительным, эти условия с учетом (14) запишутся в виде:
Для i-ой грани далее составляется система равенств (16), решение которой позволяет установить, существует ли при hi>0 вектор ai=(aik), реализующий требуемые условия для этой грани. Отмеченная ранее некорректность формально связана с тем случаем, когда hi=0 в (16). Для ее устранения достаточно случай Dpх=Dх связать с той ситуацией, когда все m граней симпекса Dх будут включены в П-множество. Это выявится после проверки всех m граней. Таким образом, определение П-множества при данном подходе сводится к m-кратному решению системы (16), или, точнее, к решению ЗЛП:[7]
где Oj – переменные, которые должны быть обращены в нуль (нулевые переменные); hi – коэффициент пропорциональности. Следует отметить, что как в первом, так и во втором случае доводить решение ЗЛП до конца, как правило, не имеет смысла. Достаточно лишь убедиться, что D>0 (1-ый алгоритм) или hi>0 (2-ой алгоритм), что гарантирует от ошибочного заключения о неоптимальности проверяемой грани. Алгоритм 2 определения p-множества 10. Читать ||aij||, ||ckj||, m 20. Для i=1 k n 30. Решить ЗЛП (17), (18) (maxh) a 40. Если hmax£0, исключить грань ei, идти к 60 50. Писать ei=epiÎDpх 60. Следующий i 70. Писать Dpх={epi} 80. Если |Dpх|¹m, идти к 100 90. Писать Dpх=Dх 100. Конец Полученные в соответствии с приведенным алгоритмом решения следующие: a1=(1/2,0,1/2,0),a2=(2/5,0,0,3/5),a3=(4/7,0,0,3/7), h1max=0,(АС); h2=0,1,(ВС); h3=1/7,(АВ). (19) Как видно из (19), грань АС не входит в П-множество (h1max>0). При одинаковой вычислительной несложности обоих алгоритмов, только первому подходу присущи следующие три особенности: – существует возможность проверить П-оптимальность любого решения Х¢ÎDх, а для ВЗЛП и найти ближайшее П-оптимальное, не прибегая к поиску всего П-множества; – случай Dpх=Dх обнаруживается в самом начале расчетов, после чего необходимость в последующих вычислениях отпадает; – без дополнительных сложностей существует возможность проверить П-оптимальность некоторой произвольной точки Х¢ÎDх в общей задаче МП (1), (2). В последнем случае достаточно в качестве массива исходных данных ||Сkj|| использовать матрицу значений производных в точке Х¢ÎDх (аппроксимация):
Ответ, получаемый в форме "да", "нет", не содержит указаний (в случае "нет") о направлении дальнейшего поиска П-оптимального решения. В случае "да" можно говорить только о локальной П-оптимальности решения вместе с проблемами, свойственными поиску глобального экстремума или П-множества. Тем не менее остается возможность поиска П-решений путем упорядоченного перебора точек ХÎDх, например по узлам числовой решетки или методом случайного поиска. В заключение отметим, что если в исходной ВЗЛП имеется m1 ограничений-равенств, то, записав их в каноническом виде Список литературы 1. Дубов Ю.А., Травкин С.И., Якимец В.Н. Многокритериальные модели формирования и выбора вариантов систем. – М.: Наука, 1986. – 295 с. 2. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. – М.: Наука, 1982. – 256 с. 3. Ларичев О.И., Поляков О.А. Человеко-машинные процедуры принятия решений многокритериальных задач МП: (Обзор). Экономика и математические методы. – 1980. – Т.16, вып. 1. – С. 127-145. 4. Гермейер Ю.Б. Введение в теорию исследования операций. – М.: Наука, 1972. – 383 с. 5. Катулев А.Н., Михно В.И., Виленчик Л.С. Современный синтез критериев в задачах принятия решений. – М.: Радио и связь, 1992. – 120 с. 6. Юдин Д.Б., Гольштейн Е.Г. Задачи и методы линейного программирования. – М.: Сов. радио, 1969. – 736 с. 7. Берзин Е.А. Оптимальное распределение ресурсов и теория игр. – М.: Радио и связь, 1983. – 183 с. 8. Карлин С. Математические методы в теории игр, программировании и экономике. – М.: Мир, 1964. – 838 с. |
http://swsys.ru/index.php?id=1106&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Использование матричных квадродеревьев для хранения площадных картографических объектов
- Инструментальные и программные средства построения сетевых моделей
- Информационная система оптимизации расписания доставки грузов от производителей сырья
- Система моделирования и оценки эффективности торговых стратегий
- Потоковый анализ программ, управляемый знаниями








 или
или 
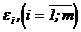 [2].
[2].



 D=-3x1+3®max, D -3 0 3 D -3 0 3 D -1 -4 0
D=-3x1+3®max, D -3 0 3 D -3 0 3 D -1 -4 0 e2=-x1-4x2+5, e2 -1 -4 5 e2 3 -4 -3 x1 1
e2=-x1-4x2+5, e2 -1 -4 5 e2 3 -4 -3 x1 1
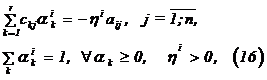


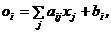 не более чем за m1 шагов ОЖИ (могут оказаться линейно зависимые), ВЗЛП приводим к виду (3), (4), но с уменьшенным на m1 числом свободных переменных.
не более чем за m1 шагов ОЖИ (могут оказаться линейно зависимые), ВЗЛП приводим к виду (3), (4), но с уменьшенным на m1 числом свободных переменных.