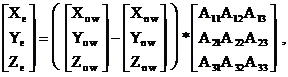Программный комплекс синтеза изображений моделируемых событий
| Левин Б.И. () - | |
|
|
|
Задача построения перспективного изображения объектов и местности по заранее известному трехмерному описанию находит широкое применение в системах моделирования событий, отображения полученной от датчиков информации и системах визуализации геоинформационных систем. Разработанный программный комплекс исходно предназначался для моделирования поведения динамических объектов в пространстве с целью получения реалистичного изображения без проведения реальных дорогостоящих экспериментов. Однако без каких-либо изменений эти же программные средства могут быть использованы для визуализации любых (например геоинформационных) данных и объектов, пространственное описание которых известно заранее. В основе комплекса находятся четыре компоненты, позволяющие провести все ступени подготовительной работы и получить последовательность изображений моделируемой сцены в реальном режиме времени. Этими компонентами являются: универсальный многооконный редактор трехмерных объектов и элементов сцены, компилятор статических и динамических объектов, компилятор сценариев поведения объектов и наблюдателя и собственно программа визуализации модели в реальном режиме времени. Для рассмотрения функционирования комплекса предварительно рассмотрим математический аппарат и базовую иерархию данных, положенные в основу проекта. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОСТРОЕНИЯ ПЕРСПЕКТИВНОЙ ПРОЕКЦИИ ТРЕХМЕРНОГО ИЗОБРАЖЕНИЯ Задача получения перспективной проекции трехмерного объекта сводится теоретически к трем умножениям расширенного вектора точки на матрицы поворота вокруг осей локальных координат и масштабирующему преобразованию полученной ортогональной проекции. Практическая реализация алгоритмов усложняется несколькими причинами. К ним относятся: ограниченность разрядности вычислителя; необходимость выполнения отсечения на границах реального экрана; необходимость расчета областей невидимости или Z-ордера точек, граней и объектов. Рассмотрим последовательность этапов, необходимых для получения реалистического изображения пространства, заданного трехмерной картой. где [Xе,Ye,Ze] – вектор объекта в системе координат наблюдателя, [Xow,Yow,Zow] – вектор объекта в мировых координатах, [Xnw,Ynw,Znw] – вектор наблюдателя в мировых координатах, A – матрица трансформации. Таким образом, коэффициенты матрицы преобразования мировых координат точки при известных координатах наблюдателя и углах направления взгляда выглядят следующим образом: А11 = Cos(g)Cos(o)+Sin(g)Cos(j)Sin(o); A21 = Sin(g)Sin(j)Cos(o)-Cos(g)Sin(o); A31 = -Sin(g)Cos(j); A12 = Sin(g)Cos(o)-Cos(g)Sin(j)Sin(o); A22 = -Sin(g)Sin(o)-Cos(g)Sin(j)Cos(o); A32 = Cos(g)Cos(j); A13 = Cos(j)Sin(o); A23 = Cos(j)Cos(o); A33 = Sin(j). Матрица трансформации образуется последовательным умножением матриц поворота на углы, характеризующие систему координат наблюдателя. В качестве характеризующих углов были выбраны три: угол o – курсовой угол, отсчитывается от оси Y по часовой стрелке, угол j – угол тангажа, между вектором взгляда и его проекцией на плоскость XY, отсчитывается от проекции вектора взгляда, на плоскости, угол g – угол крена, отсчитывается по часовой стрелке от оси Y в локальной системе координат. При этом в коэффициентах матрицы отражен факт замены осей Z и Y таким образом, чтобы ось Z была направлена по оси взгляда, ось Y вверх, а ось X вправо.
ПЕРСПЕКТИВНАЯ ПРОЕКЦИЯ ТОЧКИ Пусть необходимо получить перспективную проекцию точки A с координатами (X0,Y0,Z0) в мировой системе координат. Предполагается, что наблюдатель находится в точке B(Xn,Yn,Zn), а его взгляд направлен под углами: j – к оси Z; o – к оси Y; g – к оси X в локальной системе координат. Иными словами, j – тангаж, o – рысканье и g – крен. Тогда перевод координат точки A в координаты локальной системы осуществляется следующими действиями: P = ( A - B) * Mt; X=Xp*d/Zp ; Y=Yp*d/Zp, где Мt – матрица трансформации, d – фокусное расстояние камеры. ПЕРСПЕКТИВНАЯ ПРОЕКЦИЯ ВЫПУКЛОГО МНОГОУГОЛЬНИКА Перспективная проекция выпуклого многоугольника рассчитывается исходя из полученных координат ортогональной проекции его вершин на плоскость экрана с дальнейшим масштабированием сторон исходя из удаленности (локальной Z-координаты) его вершин. Для получения правильных проекций принимаются во внимание следующие параметры: расстояние до экрана, размеры физического экрана, размеры экрана в пикселах. Для того, чтобы избежать переполнения при расчете и получения на экране мнимой проекции объектов, находящихся за экраном, предварительно выполняется отсечение в пространстве полученного многоугольника плоскостью экрана. Для каждой грани, пересекающей экран, вычисляется точка пересечения и корректируется общее число точек многоугольника, которое может измениться после рассечения его плоскостью. После этого можно с абсолютной точностью утверждать, что координаты полученной перспективной проекции правильны и не могут вызвать переполнения заранее выбранной разрядной сетки вычислителя.
ОТСЕЧЕНИЕ МНОГОУГОЛЬНИКА НА ГРАНИЦАХ ЭКРАНА После получения корректной перспективной проекции образа необходимо произвести двойное рассечение его вертикальными и горизонтальными границами экрана с тем, чтобы избежать обработки лишних частей изображения, которые в общем случае могут значительно превышать искомое изображение по размерам. Для этого полученный многоугольник рассекается четырьмя прямыми – границами экрана, – точки пересечения с которыми, а также и их друг с другом (углы экрана), образуют новые вершины многоугольника (число его вершин также может измениться). После этого полученная проекция многоугольника готова к отображению на экран.
ПЕРСПЕКТИВНАЯ ПРОЕКЦИЯ ТРЕХМЕРНОГО ОБЪЕКТА Полный трехмерный объект, описанный полигонами его поверхностей, отображается на экран следующим образом. Вначале рассчитываются все проекции описывающих объект полигонов. При этом считается, что нормаль полигона определяется направлением описания его вершин. Так, в описываемой модели принято описание вершин по часовой стрелке. Это позволяет сразу по получении ортогональной проекции отбросить полигоны, невидимые с точки зрения наблюдателя, путем расчета Z-проекции его нормали по любым двум его сторонам. Таким образом, если нормаль окажется отрицательной, то это свидетельствует о полной невидимости полигона. Если Z-проекция нормали равна нулю, то мы видим в лучшем случае ребро полигона. Если же проекция положительная, то полигон является видимым. После расчета всех видимых полигонов выполняется специальная процедура иерархической сортировки, необходимая для определения Z-последовательности вывода полигонов на экран, что приводит к автоматическому удалению невидимых частей объекта и получению его реалистического изображения. Суть ускоренной сортировки состоит в определении конфликтующих полигонов, то есть полигонов, частично закрывающих друг друга, и в распределении их в разные группы в соответствии с Z-удаленностью ближайшей к наблюдателю точки. Таким образом, на выходе получается N групп, содержащих погруппно полигоны, не конфликтующие друг с другом, и соотношение групп, определяющее между собой порядок их вывода на экран. Такая процедура неполной сортировки позволяет получить значительный выигрыш во времени по сравнению с полной сортировкой в Z-последовательности и гарантирует правильный порядок вывода плоских полигонов при их сложном взаимном расположении. Но так как общее число полигонов, описывающих один объект, не очень велико, то в большинстве случаев могут быть успешно использованы стандартные процедуры сортировки (HeapSort, QuickSort).
ПРЕДСТАВЛЕНИЕ ТРЕХМЕРНОЙ КАРТЫ И МЕТОДЫ ОПТИМИЗАЦИИ ВЫЧИСЛЕНИЙ Формат хранения данных, представляющих собой карту поверхности, чрезвычайно важен для решения этой задачи. Правильное распределение большого массива данных позволяет не только ускорить доступ и произвольную выборку отдельных массивов, но и ускорить расчет. В описываемой модели принято иерархическое построение карты. То есть карта представляет собой сетку, состоящую из квадратов одинакового размера. Каждый квадрат содержит необходимые поля, определяющие его свойства, и ссылки на содержащиеся в квадрате объекты. Объекты представляют собой объединенные в группы кластеры, описывающие в совокупности некий пространственный объект, а кластеры – группы полигонов, обладающие определенными свойствами, расположенные либо в одной плоскости, либо имеющие малое отклонение от нее. Каждый кластер сопровождается набором специфических полей, отображающих его координаты и свойства. На самом нижнем уровне иерархии располагаются полигоны, имеющие в свою очередь специфические флаги (цвет, прозрачность и т.д.) и описываемые в общем случае обычными полигонами. Такая модель позволяет резко сократить поиск объектов, попадающих в поле зрения, и определить для них наиболее эффективные процедуры расчета. То есть первоначально определяются квадраты, находящиеся в поле зрения наблюдателя. При этом сразу фиксируется полное либо частичное попадание квадратов в зону видимости, что приводит к перераспределению объектов и кластеров, содержащихся в квадратах по специализированным процедурам, выполняющим или не выполняющим отсечение полигонов на границах экрана. После определения видимых квадратов производится их обработка в порядке удаленности от наблюдателя. Для ускорения расчета все узлы, содержащиеся в объектах, рассчитываются сразу, если проверки показали необходимость его отображения на экране, а полигоны, многократно базирующиеся на этих узлах, оперируют индексами точек. Таким образом, повторных перерасчетов одних и тех же данных не производится. При расчете одного квадрата, объекты и кластеры сортируются в Z-ордере по обычному алгоритму сортировки. Так как иерархическое разбиение уменьшает число элементов в каждой группе, то сортировка занимает не более 3% общего времени вычислений. После этого полигоны, содержащиеся в кластерах, рассчитываются и выводятся на экран. Такой подход позволяет, с одной стороны, получить перекрытие рассчитываемых точек только на границах квадратов, что составляет не более 2% от общего числа точек. И с другой – отсеять все невидимые или частично видимые объекты на возможно ранней стадии расчетов, что значительно повышает производительность системы. Кроме этого, в параметрах объектов и кластеров задается ряд дополнительных флагов и значений, позволяющих резко оптимизировать расчет. Например, к таким параметрам относятся минимальное расстояние до наблюдателя, начиная с которого полигон или кластер изображаются точкой или превращаются в линию, и максимальный размер объекта. Если учесть, что объекты в квадратах, кластеры в объектах и полигоны в кластерах отсортированы по размеру, то мы получаем простой и эффективный алгоритм прекращения расчета кластеров и объектов в связи с их удаленностью от наблюдателя. Применяется также, целый ряд вспомогательных алгоритмов, позволяющих ускорить векторный расчет взаимосвязанных узлов, расчет по вызову, углубленный предварительный анализ объектов. Следует отметить, что реальный объект, описываемый в карте, в зависимости от сложности его структуры может быть представлен как одним полигоном и отдельным кластером, так и группой кластеров или группой объектов. ИСПОЛЬЗОВАНИЕ ОСВЕЩЕННОСТИ, ТЕНЕЙ И ФАКТУРЫ ПОВЕРХНОСТЕЙ На этапе подготовки карты в описанном формате производится несколько дополнительных преобразований, выполняемых один раз и позволяющих повысить реалистичность изображения. В число расчетов входят дополнительные проверки на непересекаемость объектами границ квадратов, расчет дистанций невидимости и сортировка кластеров и полигонов согласно этой дистанции. На этапе загрузки производится перерасчет и коррекция цветов объектов с учетом цвета и положения источника освещения и ориентации полигонов в пространстве. В специальных случаях допускается образование специальных объектов, представляющих собой тени, и дополнение их к существующей карте. Так как такой расчет производится только один раз при загрузке системы, то время решения этих задач не критично, хотя и не является большим. Таким образом, общая цветовая палитра карты пополняется новыми цветами в зависимости от освещенности полигонов. Для отображения неравномерной поверхности используется чередующаяся композиция цветов. Это становится возможно благодаря ориентации на 32-битную архитектуру и свойства алгоритмов заполнения полигонов, для которых выгоднее использовать 4-байтное цветовое слово. Наиболее скоростным в данном случае остается использование монохромной палитры, позволяющей оперировать индексами цветов как самими цветами, то есть имеющей однозначное соответствие между индексом цвета и его RGB-компонентами. ПОСТРОЕНИЕ ДИНАМИЧЕСКИХ ОБЪЕКТОВ При построении изображений динамических объектов следует учитывать также его собственное местоположение и ориентацию в пространстве. Иными словами, перед расчетом точек объекта необходимо произвести предварительный перерасчет их из локальной системы координат объекта в мировую систему. Матрица трансформации для динамического объекта образуется аналогично описанной, но учитывая, что повороты необходимо совершать в обратном направлении и не следует заменять оси координат, так как в отличие от системы координат наблюдателя оси динамического объекта не изменяются. После получения предварительно рассчитанных точек остается определить квадрат, которому в данный момент принадлежит этот объект, и включить его в множество объектов данного квадрата, подлежащих сортировке в Z-порядке. Совокупность перечисленных выше алгоритмов и методов дает возможность получить реалистичное изображение местности при относительно малом объеме расчетов. Это позволяет производить такие расчеты в реальном масштабе времени с частотой 20-25 кадров в секунду и применять описанный алгоритм в системах моделирования, эмуляции и системах управления движущимися объектами. К достоинствам описанного решения следует в первую очередь отнести гибкость алгоритмов, позволяющую в зависимости от требования и наличия вычислительных мощностей производить построение изображения с разной степенью детализации вплоть до очень высокой. По сравнению с алгоритмами масштабирования фактуры поверхности данный метод не имеет недостатков, связанных с ухудшением качества изображения на малых расстояниях до объекта, при том, что является гораздо более скоростным. Качество аппроксимации объекта выбирается исходя из требований к изображению и мощностей имеющихся вычислительных средств и может варьироваться в очень широких пределах. Для большей универсальности последние версии программ ориентированы также и на использование фактуры поверхности, хотя ее применение связано с рядом негативных эффектов, проявляющихся на малом расстоянии до объекта. Кроме этого, к достоинствам данного алгоритма следует отнести очевидную легкость его распараллеливания, так как каждый квадрат, объект, кластер и полигон считаются на своем уровне независимо от других одноуровневых элементов, что позволяет использовать многоуровневое распараллеливание расчетов. Последнее свойство активно исследуется с целью переноса программного комплекса на параллельные высокопроизводительные транспьютерные системы.
РЕАЛИЗАЦИЯ АЛГОРИТМОВ ПОСТРОЕНИЯ ИЗОБРАЖЕНИЙ Совокупность описанных алгоритмов послужила базисом для создания версии программного комплекса визуализации. В состав комплекса вошли следующие компоненты. 1. Многооконный редактор трехмерных объектов. 2. Компилятор статических и динамических объектов. 3. Редактор палитры. 4. Компилятор сценариев поведения объектов. 5. Программа визуализации. Таким образом, посредством перечисленных программ становится возможным проведение моделирования событий и получение изображений требуемого сценария. Редактор MAPEDIT предназначен для создания трехмерных объектов и элементов сцены и для записи полученных объектов в текстовом формате, совместимом с входным языком компилятора объектов. Требования к аппаратуре, предъявляемые редактором: IBM PC/AT 386 или выше, мышь. Редактор управляется командами с клавиатуры и мышью. Программа MAP2BIN предназначена для получения файлов данных статических сцен и динамических объектов в формате, используемом в программе визуализации сценария. Компилятор входного языка описания поведения SCENARY позволяет получать ко- мандные файлы поведения объектов, используемых программой визуализации. Программа визуализации VISUAL предназначена для получения динамического изображения эксперимента. В ходе визуализации возможно как автоматическое (по сценарию), так и ручное управление положением точки наблюдения. При построении изображения обрабатываются дополнительные эффекты, повышающие реалистичность изображения, такие как градации освещенности неба, земли, учет кривизны земной поверхности, сокрытие в дымке удаленных объектов, перерасчет освещенности динамических объектов и ряд других. Проведенные эксперименты показывают высокую эффективность разработанных алгоритмов. Так, достаточно загруженная сцена размером 18´18 километров, с находящимися на ней 40 статическими и 5 динамическими объектами, суммарным весом более 7000 узлов и 3000 полигонов обрабатывается на машине 386DX/40 со скоростью 14 кадров в секунду, а на машине 486DX2/66 –38 кадров в секунду. |
http://swsys.ru/index.php?id=1118&lang=%2C&page=article |
|