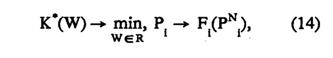Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование и оптимальное проектирование обучающих курсов
Аннотация:
Abstract:
| Авторы: Палюх Б.В. (pboris@tstu.tver.ru) - Тверской государственный технический университет (профессор), г. Тверь, Россия, доктор технических наук, Чохонелидзе А.Н. (444595@pochtf.ru) - Тверской государственный технический университет, г. Тверь, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 13529 |
Версия для печати |
Традиционные формы обучения — лекции, практические и лабораторные занятия, курсовые, дипломные работы и так далее - хорошо отработаны в течение длительного времени и имеют огромное значение в учебном процессе. Они доказали свою надежность при подготовке научных кадров [1]. Однако дальнейшее развитие нашего общества приводит к бурному росту количества информации и к ее качественному переосмыслению. В связи с этим необходима коренная перестройка всех учебных программ, компьютеризация всех звеньев образования [2]. Это позволит существенно повысить эффективность учебного процесса за счет улучшения управления процессами усвоения и использования знаний. Среди большого арсенала разнообразных форм и средств обучения особое место занимает обучение с использованием средств вычислительной техники. Данный подход дает следующие основные преимущества: - позволяет проводить обучение широкой аудитории слушателей; - ведет к сокращению затрат времени на внедрение новых учебных курсов; - позволяет наглядно иллюстрировать новые понятия; - развивает навыки работы со средствами вычислительной техники (СВТ); - позволяет восполнить нехватку достаточного количества квалифицированных преподавателей. К сожалению, из-за несовершенства теории автоматизированного обучения сейчас трудно однозначно установить место обучающих систем в учебном процессе. Требуется проведение специальных исследований различных аспектов компьютерного обучения, в том числе их классификации. Рассмотрим классификацию автоматизированных обучающих систем (АОС) по функциональному признаку (рис.1). На базе предлагаемой классификации опишем основные преимущества и недостатки распространенных в наше время АОС и коротко остановимся на их функциональных характеристиках. . Обучающие системы предназначены в основном для обучения понятиям и навыкам на базе информационно-справочных сред [2]. В основе систем подобного типа лежит интеллектуальный, учебный курс, обладающий широким языком запросов и богатым набором ассоциативных связей в базе данных. В качестве изъянов в подобных системах можно отметить их недостаточную гибкость и чувствительность к настройке. Системы консультирующего типа чаще всего предназначены для оказания контекстной помощи или выдачи требуемой информации по запросу пользователя, при этом возможно демонстрационное решение задач с их последующим решением для каждого шага [3]. Чаще всего системы подобного типа включают в себя информационно-справочную подсистему, подсистему контекстной подсказки и модель обучаемого. К недостаткам можно отнести сложность наполнения подобных систем неквалифицированным пользователем. Системы диагностирующего типа являются дальнейшим развитием систем консультационного типа. Они дополнены расширенным интерфейсом, фиксацией знаний и умений обучаемого и диагностикой ошибок обучаемого [4]. На практике эти системы часто называют интеллектуально-тренирующими или экспертно-тренирующими. В качестве слабого места в таких системах можно отметить невозможность генерации знаний самой системой. Обычно генерация осуществляется преподавателем при настройке системы, что усложняет индивидуализацию знаний. Управляющие системы являются наиболее сложными из существующих типов АОС и предназначены в основном для управления процессом обучения с помощью средств вычислительной техники [5]. Она содержит в себе все компоненты рассмотренных ранее систем, но дополнена в свою очередь диагностирующей экспертной системой знаний о целях функционирования системы с учетом стратегии обучения. В качестве недостатков систем подобного типа можно отметить их громоздкость и сложность в эксплуатации. Системы сопровождающего типа отслеживают деятельность обучаемого при работе в некоторой инструментальной среде, содержащей все компоненты реальной системы, с оказанием помощи при обнаружении ошибочных действий обучаемого [6]; сопровождающая система содержит все компоненты экспертной системы, но, в отличие от нее, не знает конечной цели деятельности пользователя и должна ее прогнозировать.
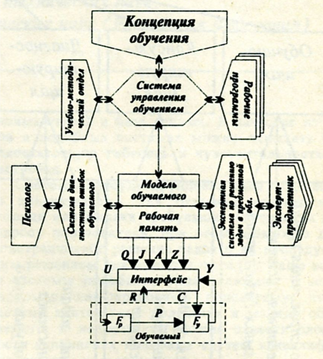
Рис.1. Классификация АОС по функциональному признаку Интегрированные обучающие системы (ИОС) в основном свободны от указанных выше недостатков и, несмотря на некоторую структурную сложность, позволяют значительно расширить функции АОС по диагностике ошибок и прогнозированию целей деятельности пользователя [5]. В плане генезиса интегрированные системы можно рассматривать как дальнейшее развитие систем управляющего, консультирующего и сопровождающего типов [1]. При этом интегрированной обучающей системой мы будем называть программную среду, реализующую ту или иную педагогическую цель на основе знаний в некоторой предметной области, в области диагностики знаний обучаемых и в управлении обучением и демонстрирующую поведение на уровне экспертов. При этом в научном плане можно выделить следующие основные задачи: - анализ существующих в настоящее время обучающих систем с точки зрения возможности их использования в динамически изменяющейся структуре высшей школы; - разработка структуры интегрированных обучающих систем; - математическое моделирование процесса обучения в высшей школе; - представление и обработка знаний в предметной области, составляющей предмет обучения; - разработка методов контроля и диагностики ошибок обучаемого; - разработка методов управления процессами обучения. В основе структурной организации интегрированных обучающих систем лежит математическая модель процесса обучения. На понятийном уровне ее можно сформировать следующим образом: - на основании текущего состояния обучаемого и методики обучения генерируется очередная задача, требующая ответных действий обучаемого; - ответ обучаемого сравнивается с эталонным решением, и на основании различий диагностируются ошибки обучаемого; - по результатам диагностики корректируются текущие характеристики обучаемого. В соответствии с данной моделью процесса обучения ИОС можно рассматривать как совокупность трех взаимодействующих обучающих сред: - по решению задач в изучаемой предметной области; - по диагностике ошибок обучаемого; - по планированию процесса управления обучением. На рисунке 2 представлена формализованная структурная схема ИОС подобного типа. Введем основные предпосылки и упрощения, принятые при формализации модели. Будем считать объект обучения специфическим запоминающим устройством, обладающим рядом свойств, которые проявляются лишь в процессе его обучения [7]. Само обучение представим в виде процесса управления в обстановке неопределенности, для чего используем методы адаптации. Такой подход требует применения методов теории управления к процессу обучения и возможен лишь при условии формализации объекта обучения.
Рис.2. Структурная схема ИОС где: U, С - каналы управления, обучения и контроля соответственно; Y - канал обратной связи в виде результатов контроля; R - канал управления обучаемым; A - алгоритм управления; Z - цель обучения; Q - относительный вес обучающей информации; J - обучающая информация; P - состояние обучаемого; Fy, Fp - операторы состояния и результатов контроля обучаемого соответственно. Поэтому начнем рассмотрение вопроса с обоснования необходимости разработки модели обучающего процесса. Пусть при этом предметом обучения являются п +1 заданных порций обучающей информации: J = (j1, …, jn-1, jn. …, jn+1) (1) у которых известны их относительные веса:
Q = (q1, …, qn-1, qn. …, qn+1) (2) причем:
где q1 - априорная мера частоты использования знаний в практической деятельности обучаемого, q = 0, 1. На основании принципов декомпозиции сложной системы представим процесс обучения состоящим из двух повторяющихся этапов. Первый этап: передача ученику порции обучающей информации
N= 1,2…n Второй этап: контроль за обучением
Результаты контроля представлены в виде двоичного вектора для канала обратной связи:
Модель обучаемого, представленная на рисунке 2, задается в виде операторов Fp и Fy , а состояние обучаемого оператором Р: P=Fp(U), (7) Y= Fy(P,C). Определим цель обучения исходя из состояния объекта обучения:
то есть необходимо знание порций информации с вероятностью не меньше заданной (1-εi). С прикладной точки зрения наиболее важной оказывается другая цель: где К - интегральный критерий эффективности знаний обучаемого;
Где Pi – вероятность незнания порции информации на N-том шаге обучения, qi – частота использования знаний. В Этом случае знание характеризует вероятность незнания, обнаруживаемого обучаемым а практической деятельности. Это цель задается числом ε. Наилучшие результаты дает комбинация двух форм целей (9) и (10), например в виде
то есть заданное множество V порций информации следует знать с заданной вероятностью и одновременно с заданным ограничением на вероятность незнания в практической деятельности. Алгоритм обучения должен обеспечивать минимум шагов обучения, необходимых для достижения цели Z. Для этого цель представим в виде: K*(P,Q)<ε, (12) где
α – коэффициент штрафа ψ(х) - функция знаний, х - значение аргумента в наперед заданном интервале. Минимизируем значение К* в рамках выделенного ресурса R на каждом шаге обучения:
где U - порция обучающей информации. Ее решение образует порции информации, которые выдаются обучаемому за один шаг. Эту задачу целесообразно решать простой заменой для такого множества W, при котором значение минимально W€R, то есть
где W - множество обучающей информации. Эта комбинаторная задача при линейной функции f1 решается упорядоченным перебором J1, то есть не зависит от n. Эффективность такого решения прямо зависит от адекватности модели. Более того, в процессе обучения сама модель может изменяться. Неопределенность факторов заставляет обращаться к процедуре корректировки модели на базе получаемой при контроле информации. Процесс адаптации осуществляется рекуррентным способом: FN+1 = FN + ∆FN+1 (15) Где ∆ FN+1 – изменение функции на (N+1)-м шаге обучения, которое зависит от результатов контроля (8): ∆ FN+1 = J(YN, FN) (16) В заключение следует отметить, что адаптация системы обучения к индивидуальным свойствам обучаемого дает возможность минимизировать время обучения. Таким образом, использование интегрированных обучающих систем дает возможность с минимальными затратами преодолеть порог трудности обучения и приспособление процесса обучения к особенностям каждого конкретного обучаемого. При этом сначала определяется индивидуальный объем обучающей информации I. Ее можно пропустить, считая РNi =0, i=l, ..., n, то есть считать абонента полностью необученным (удлиняет обучение). Обучение состоит в том, что на каждом шаге система строит согласно алгоритму для каждого конкретного обучаемого информационное поле, по которому впоследствии определяются промежутки между сеансами обучения и коррекции вектора вероятностей незнания, а также время Тn, затраченное на заучивание предыдущей порции и свой ресурс, то есть время, планируемое на выполнение следующего задания Т N+1плановая. Далее осуществляется контроль по критериям качества обучения К. Когда этот критерий достигает требуемого уровня Е, обучение заканчивается и обучаемый получает протокол с информацией о результатах тестирования. Предлагаемый в работе подход к проблеме создания автоматизированных обучающих курсов доведен до логического конца: разработано программное средство универсального назначения (ПС "Экзамен"). ПС "Экзамен" состоит из трех независимых модулей - учебника, задачника и экзаменатора - интегрированных в рамках единой оболочки. Объектная ориентация осуществляется самим пользователем путем наполнения системы конкретной предметной областью. Зависимость между знаниями обучаемых и численной оценкой, не имеющая явно выраженной закономерности, может быть скоррелироваина путем введения бальной оценки ответов экзаменуемых, зависящих в свою очередь от весовых коэффициентов, учитывающих сложность предлагаемого вопроса для респондентов с различной степенью подготовки. ПС не накладывает никаких ограничений на объемы обучающих курсов, кроме как возможностей вашего компьютера. Список использованной литературы 1. Петрушки В.А. Экспертно-обучающие системы. - Киев: Наук, думка, 1992. - 196 с. 2. Control for Intelligent Tutoring Systems: A Blackboard-Based Dynamic Instructional Planner // Blerman D., Breuker J., Sandberg J. Artificial Intelligence and Education. Proc. 4th Int. Conf. on AI and Education (24-26 May 1989, Amsterdam: IOS, 1989. - P. 150-168. 3. Программированное обучение (Анализ зарубежного опыта). - М.: Наука, 1992. - 208 с. 4. Основы статической теории обучения и контроля знаний. - М.: Высш.шк., 1981. - 262 с. 5. Инструментальные средства для создания экспертно-обучающих систем // Интеллектуальные системы в задачах проектирования, планирования и управления в условиях Казань: НПО "Волга", 1990 неполноты информации. С. 112-115. 6. Свиридов А.П. Основы статистической теории обучения и контроля знаний. - М.: Высшая школа, 1986. — 176 с. 7. Растригин Л.А. Обучение как управление // Методы школы. - Рига: Изд-во РПИ, 1985. - С. 13-36. 8. Тарасеико Т.С., Эренштейн М.Х. Исследование сходимости одного процесса обучения // Проблемы случайного поиска. - Рига, Г978, Вып. 6. - С.267-274. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=1154&page=article |
Версия для печати |
| Статья опубликована в выпуске журнала № 2 за 1994 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Учебный банк: технологии изучения банковских систем и телекоммуникаций
- Оптимизация обработки информационных запросов в СУБД
- Алгоритмы и процедуры построения билинейных моделей непрерывных производств
- Вычислительный интеллект: немонотонные логики и графическое представление знаний
- Зарубежные базы данных по программным средствам вычислительной техники
Назад, к списку статей