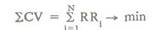Проблемы расширения пакета прикладных программ для решения задач моделирования на основе МГУА
| Ивахненко А.Г. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Алгоритмы для четких объектов с постоянными параметрами Программы моделирования на основе метода группового учета аргументов (МГУА) предназначены для решения задач прогнозирования случайных процессов и событий и задач восстановления закономерностей. Число переменных обычно превышает число строк (точек) таблицы в несколько раз. Практика показывает, что именно задачи обработки коротких выборок являются наиболее актуальными. Несмотря на малую длину выборки, в результате перебора множества моделей-кандидатов должна быть выбрана достаточно сложная, оптимальная по критерию модель [7]. Результаты вычислительного эксперимента
На рис. 1 представлены кривые изменения критерия регулярности Выбор подхода к моделированию Качественно рис. 1 остается действительным для всех известных критериев; более того, кривая изменения критериев (при отсутствии помех) при 62 = 0 для всех критериев остается одинаковой. Таким образом, в случае неточных или неполных данных выбор критерия перебора сказывается только на выборе прогнозирующих моделей. Кривые на рис. 1 достаточно пологие (минимум — не острый), поэтому все критерии дают практически приблизительно один и тот же выбор оптимальной прогнозирующей модели. При этом имеет значение только то, что для прогноза применялась бы модель более простая, чем физическая. Поэтому удивляет все возрастающее количество предложений новых критериев, особенно со стороны японских ученых [9]. Разрабатываются критерии информационного типа для того, чтобы дать тот же результат выбора модели, что и точностные критерии математической статистики, не требующие разделения выборки на части. При короткой выборке данных нет проблемы ее оптимального разделения на части; есть проблема априорного выбора подхода к моделированию. В случае отсутствия любой информации, кроме выборки данных, единственно возможным является точностной подход, при котором модель должна как можно более точно отражать выборку данных. Точностной подход, основанный на применении точностных и информационных критериев, доминирует во всех научных разработках. Если известно, что данная короткая выборка данных не очень достоверна, а следующая может нести в себе изменения информации, то следует применить робастный подход, основанный на применении критериев дифференциального типа, например критерия непротиворечивости:
Этот критерий требует, чтобы модель, полученная на подвыборке А, как можно меньше отличалась от модели, полученной на подвыборке В. Это гарантирует устойчивость результатов моделирования на последующих выборках данных. При робастном подходе оптимальная модель более проста, чем при точностном подходе, особенно при больших помехах. Комбинированный подход означает выбор оптимальной модели по критериям дифференциального типа из множества моделей, отобранных по точностным и информационным критериям. В качестве ограничения часто используется критерий вариации: Рис. 1. Результаты вычислительных экспериментов АВ — критерий регулярности S — сложность полиномиальной модели - (число н степень слагаемых) Кривые построены экспериментально при постепенном изменении сложности полиномиальной модели S и интенсивности помех 8 -Точка S отвечает истинной физической модели, а минимумы кривых О , О , О , О определяют оптимальную сложность прогнозирующих моделей: при увеличении помех оптимальной становится более простая модель.
где С — экзаменационная часть выборки (две-три строки), у — фактические данные, у — прогноз по модели, у — среднее значение (исключая точку прогноза). Прогнозы, для которых RR>1,O, считаются недостоверными, и соответствующие им модели исключаются из перебора, выполняемого по основному критерию дифференциального типа. Задача оптимального разделения выборки данных для расчета значения критериев Проблема разделения выборки данных на две лодвыборки (при коротких выборках данных) полностью решена. При точностном подходе в подвыборку А входят все точки, кроме одной, а в подвыборку В — только одна точка: А = N-1 В = 1 Моделирование повторяется N раз при выделении в подвыборку В всех точек по одной, и результаты усредняются (точностной критерий перекрестного определения cross validation criterion). При робастном подходе выборка делится на А = N/2 и В = N/2. Точки ранжируются в ряд по дисперсии. При решении задач прогнозирования и восстановления зависимостей в подмножество А поступают точки с большей дисперсией, а в подмножество В — с меньшим ее значением. При решении задач кластеризации и распознавания образов точки поступают в А или В через одну по очереди, чтобы получить близкие по дисперсии подмножества. Критерии дифференциального типа, не требующие разделения выборки на части А и В Отказ от разделения выборки на части позволяет получить достаточно сложные модели (даже при короткой выборке) при наиболее экономном ее использовании. Во время решения задачи прогноза процессов выборка данных может быть подвергнута некоторой математической обработке с сохранением основных частот процесса (главные собственные числа), хотя соотношение амплитуд частотных составляющих может меняться. Переменные, получаемые в результате такой обработки, называются инструментальными. При робастном подходе можно не делить выборку на две равные части, а преобразовать ее в равные по размерности bi борки двух инструментальных переменных. Один из способов — использование под выборку первых разностей и первых сумм значений переменных выходной выборки. В подвыборку А включают первые разности переменных, а в подвыборку В — первые суммы. В настоящее время наиболее разработан способ, при котором используется дискретизация (ранжирование) переменных на N и на N/2 уровней (рангов) [12]. Учет особенностей прогноза многомерных процессов Основные алгоритмы МГУА ("Комби", "СМЛ" и др.) можно назвать одномерными в том смысле, что в результате их применения находится модель в виде одного уравнения, в котором выходную величину указывает человек (эксперт). В отличие от этого алгоритм объективного системного анализа (ОСА) [4, 8, 12] направлен на поиск модели в виде системы уравнений, причем все переменные, указанные в выборке данных, считаются выходными по очереди, с тем чтобы по критерию найти оптимальное их множество. Алгоритм ОСА использует так называемые неявные шаблоны, при которых в число возможных регрессоров включаются не только запаздывающие аргументы, но и будущие значения всех переменных. Это значительно расширяет эффективность моделирования. Тем не менее в алгоритме ОСА еще требуется: ■ расширение множества регрессоров-кандида- тов с одновременным переходом к использова нию многорядных алгоритмов МГУА вместо комбинаторного алгоритма для сокращения объема перебора. В пределах заданной глубины учета предыстории должны быть просмотрены все прошлые, текущие и будущие значения на блюдаемых переменных, особенно внешних воздействий (последнее является аналогом уче та производных в правой части уравнений дина мика систем управления в соответствии с тео рией инвариантности); • введение вариации глубины учитываемой предыстории с возможным варьированием для каждой переменной отдельно; • принятие комбинированного подхода, т.е. применение дифференциальных критериев не противоречивости или баланса переменных при ограничении на вариацию прогнозов RR<1,O, подлежащих перебору; • применение критерия баланса дискретизаций, не требующего деления выборки на две части; применение многократного повторения алго ритма ОСА с исключением выделенных эффек тивных переменных при каждом последующем применении алгоритма [5] и возможное получе ние при этом многомерного прогноза, т.е. прог ноза многих переменных; ■ введение перебора моделей от более слож ных к более простым с целью исключения "эф фекта первого ряда". Он заключается в том, что при малой сложности моделей (когда еще не образована система уравнений) плавный ха рактер кривых (рис.1) часто нарушается, что может привести к ошибке при выборе модели оптимальной сложности. С учетом указанных обстоятельств алгоритм ОСА будет наиболее эффективным при решении задач многомерного прогноза, но только для хорошо определенных технических (промышленных) объектов. Программу ОСА можно легко приспособить для решения задач в реальном масштабе времени на машинах, допускающих параллельную обработку информации. Решение задач» поиска глобального экстремума Многомерная экстремальная характеристика может быть результатом действия генератора случайных чисел или отражать некоторую закономерность. В первом случае корреляции меж- ду значениями функции нет и алгоритмы МГУА применить нельзя. Во втором случае при помощи алгоритмов МГУА по части точек может быть восстановлена скрытая в них зависимость — следовательно, можно найти все ее точки, в том числе и глобальный экстремум. Моделирование логико-динамических систем Сказанное откосится к задачам обработки данных одной короткой выборки наблюдений; при этом от разработчика модели не требуется никаких детальных указаний, он должен только выбрать подход, т.е. указать критерий перебора. 8 логико-динамических системах наблюдения представлены несколькими выборками данных, связанными логическими переходами. Перебор множества моделей-кандидатов таков, что в процесс выбора моделей требуется более активное вмешательство человека. Чем мощнее компьютер, тем меньше потребность в интерактивных (диалоговых) алгоритмах моделирования. Алгоритмы для нечетких объектов с изменяющимися параметрами Как следует понимать Викеровскую идею кибернетики? Так случилось, что идея Н.Винера [1] об общем подходе к математическому исследованию биологических и технических систем попала в руки тех, кто воспитывался на материалах математической физики, имеющей дело с так называемыми детерминированными (или четкими) законами. Первое, что они сделали, — это применили алгебраические и дифференциальные уравнения математической физики (уравнение маятника, диффузии и др.) к биологическим и природным системам. Но оказалось, что эти уравнения хорошо описывают технические системы, но не совсем подходят для описания природных объектов [11]. Идею Винера теперь следует понимать так: природные, биологические объекты можно исследовать при помощи математики, но язык (аппарат) математики должен быть выбран соответственно закону адекватности. Применительно к четким объектам: для M:N = l:10 (M — число переменных) выбираются метод наименьших квадратов (регрессионный анализ), комбинаторный алгоритм МГУА; для M = N — классические методы математической физики, метод избранных точек; для M:N = S:1 — многорядные (итерационные) алгоритмы МГУА. Для нечетких объектов: при M:N^5:1 выбирается алгоритм многорядной теории статистических решений; при M:N>10:l — Паттерн- и кластер-анализы, алгоритмы МГУА с комплексированием аналогов для прогноза процессов и событий. Закон адекватности описания объекта и математического языка его исследования впервые был дан в работе английского ученого Стаффорда Бира [6, 11]. Природные, экологические объекты относятся к нечетким (размытым) объектам с изменяющимися параметрами. Адекватный математический аппарат для очень размытых объектов, называемый паттерн-анализом [11], предложен проф. В.В.Налимовым. Кластер-анализ [2] можно рассматривать как развитие паттерн-анализа: он учитывает размытый характер объекта, так как использует переменную ширину паттернов. Выбор математического языка моделирования по форме матрицы выборки данных Будем называть многомерными нечеткими (размытыми) объекты, которые не удается наблюдать достаточное время для того, чтобы получить алгебраический минимум точек (квадратную матрицу) и у которых в то же время нельзя сократить множество выходных переменных без потери интересующей нас информации. Например, погоду не удается наблюдать больше трех-четырех суток без существенного изменения структуры и параметров системы уравнений, при этом нельзя исключить ни одну из семи переменных совокупности признаков: температуру, давление, влажность, две составляющие направления и силы ветра, а также облачность (число часов солнечного сияния). Мера нечеткости объекта и выбор адекватного математического аппарата Размер минимального шага измерения данных определяется многими причинами, среди которых немалую роль играет организация мониторинга и уровень развития измерительной техники. Практикой уже установлен этот размер: в экономике им является квартал, в экосистеме — сезон, в демографии — год и т.д. Бесконечно большая выборка данных означала бы бесконечно долгое время наблюдения за объектом, что не было бы эффективным, И все-таки в технических системах часто можно считать выборку бесконечно длинной: например, колебания маятника можно наблюдать бесконечно, так как его структура и параметры, подлежащие определению, быстро не изменяются. Для описания маятника или системы маятников нет ничего лучше дифференциальных уравнений или их разностных аналогий [3], но в практике моделирования все чаще используется поступление заказов на модели нечетких объектов с изменяющейся структурой или параметрами при большом числе наблюдаемых и выходных переменных, которые компьютер должен выбрать без помощи эксперта. Степень нечеткости объекта Нечеткий (размытый) объект — это в большинстве случаев с изменяющимися во времени параметрами. Обозначим число шагов наблюдения, при котором параметры объекта можно считать достаточно постоянными, N, а число переменных — М. Тогда выборка данных может быть представлена матрицей размером NxM элементов. При N Асимптотические исследования. В связи с направленностью МГУА на решение задач моделирования при короткой выборке данных ис- следования изменения вида кривых (рис.1) в асимптотике, т.е. при увеличении числа строк выборки, не представляют большого интереса. Тем не менее интересен результат исследований В.С.Степашко [15]: при увеличении выборки все кривые сходятся в узкий пучок, почти совпадающий с нижней кривой, полученной при отсутствии помех 82 = 6. Можно сделать вывод, что при длинных выборках данных оптимальной прогнозирующей моделью является точная физическая модель, при коротких выборках нужна более простая модель, адекватная заданному объекту. Выбор адекватного математического языка моделирования Математический аппарат, как и объект, может иметь разную степень нечеткости. Регрессионный анализ применим для матриц размером IV > М, причем по требованию метрологии число строк N должно превышать число столбцов М не менее чем в пять-десять раз. Классические понятия дифференциальных уравнений и их разностных аналогов оперируют с квадратными матрицами, где M = N. Многорядньге (итерационные) алгоритмы МГУА, использующие поликомы, могут обрабатывать матрицы, где N Многорядные алгоритмы МГУА, использующие формулы Байеса (или статистической теории Вальда), позволяют обрабатывать еще более короткие выборки, например, при числе строк в десять и более раз меньшем числа переменных. Это послужило основанием построения многорядной теории статистических решений. Соответствующие алгоритмы МГУА успешно применяются для прогноза уровня концентрации пестицидов в почве (N = 4 точки, М = 22 переменных) и для идентификации процессов шинного производства (N = 5 точек, М = 20 параметров). В случае зависимых переменных х и х. используются так называемые переменные парных взаимодействий х = \/х х.. Для соблюдения закона адекватности при недостаточной степени нечеткости аппарата и еще большей размытости объекта следует применить алгоритмы МГУА на основе паттерн-анализа В.В. Налимова или кластер-анализа. Обратное превращение ослабленного прогноза в детальный происходит при помощи поиска и комплексирования аналогов в предыстории. Комплексирование означает аппроксимацию короткой выборки, точек пространства прогнозов аналогов. Паттерн- и кластер-анализы используют технику скользящего окна наблюдения многомерных процессов, где число наблюдаемых переменных не ограничено, а оптимальная ширина окна (т.е. паттерна или кластера) легко выбирается при помощи индуктивного (переборного) метода. Эта задача не решается дедуктивными, аналитическими методами [13]. Программы МГУА на основе паттерн- и кластер-анализов разработаны не только для прогноза случайных многомерных процессов, но и для прогноза многомерных событий (например для выяснения результатов лечения больных). Таким образом, в арсенале исследователя должны быть все алгоритмы и программы МГУА, чтобы для каждой задачи найти адекватный математический аппарат. Алгоритм объективной компьютерной кластеризации (О К К) Динамической кластеризацией называется разделение выборки данных на полосы-кластеры, точки которых имеют некоторую общность. Такое разделение представляет интерес для изучения процессов в объекте на размытом языке перехода одного кластера в другой. Так, благодаря применению ОКК при выборке данных об экономике ГДР выяснилось, что до 1975 года размеры кластеров увеличивались, а затем стали уменьшаться, т.е. экономика стала более нестабильной [14, 15]. Структура алгоритма ОКК во многом похожа на структуру алгоритма ОСА [2], отличаясь лишь тем, что вместо полиномов используется размытый язык кластеров. Учет размытости характера природных, экономических и других объектов и переход к непараметрическим алгоритмам МГУА Алгоритмы МГУА, включая ОСА, основаны на переборе решений дифференциальных и интегральных уравнений [10] либо их разностных полиномиальных аналогов, что часто противоречит закону адекватности. Кроме того, значительные трудности возникают при оценке коэффициентов разностных уравнений: требования регрессионного анализа (полный набор регрес-соров и действие помех только на выходную величину) при переборе полиномиальных моделей удоалетворить нельзя, и оценки получаются неточными, смещенными. Поэтому, особенно в случае "размытых" объектов, в качестве математического описания лучше всего отказаться от полиномов и использовать саму выборку данных и аппроксимацию (комплекси-рование) некоторых точек пространства прогнозов. Перебор множеств переменных и числа комплексируемых аналогов, по алгоритму и критериям комбинаторного алгоритма МГУА, повышает эффективность паттерн-анализа при решении задачи детального прогноза многомерных случайных процессов в указанных объектах.
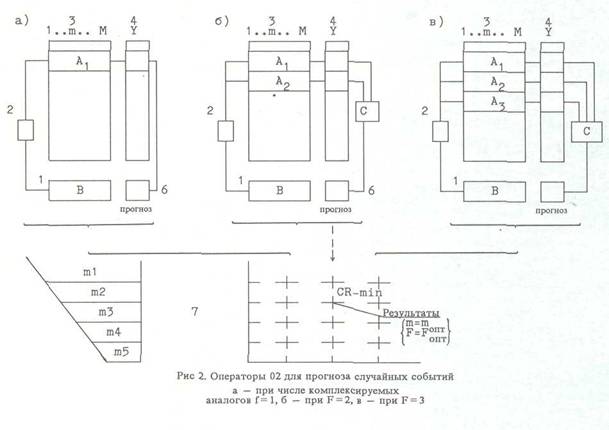
На рис.2 представлен комбинаторный алгоритм МГУА с комплексированием прогнозов аналогов при точностном критерии перекрестного определения
б) ранжирование паттернов (строк) по корреля ционному критерию и выбор аналогов F, в) самоорганизация (перебор) множеств пере менных m и числа комплексируемых аналогов F, г) комплексирование прогнозов по сплайну (или по комбинаторному алгоритму МГУ А) и выдача прогноза. Нетрудно составить аналогичную схему комбинаторного алгоритма МГУА с использованием комплексирования аналогов, реализующую робастный подход, т.е. критерий баланса дискретизации. Разрабатываются алгоритмы многорядных (итерационных) алгоритмов МГУА с использованием комплекскрования прогнозов аналогов — как точностной, так и робастный. Прогноз процессов и событий При поступлении абитуриента в ВУЗ имеется выборка данных о его успеваемости в школе. Как он будет успевать в ВУЗе? Чтобы ответить на этот вопрос, достаточно найти его аналог в предыстории, т.е. в банке данных тех абитуриентов, которые по всем показателям и оценкам были к нему ближе всех. Этот пример показывает особенности задач, в которых нас интересует не будущее значение регрессоров (прогноз процесса), а будущее событие, зависящее от них. Такие важнейшие задачи, как прогноз урожая, выбор оператора для управления процессом, выбор промышленного агрегата или машины и многие другие относятся к задачам прогноза случайных событий. Для решения задач подобного типа разработаны алгоритмы МГУА на основе комплексирования аналогов. Список литературы 1. Винер Н. Кибернетика, или управление и связь в живот ном н машине. М.: Сов. радио, 1968. 326 с. 2. Жамбю М. Иерархический кластер-анализ и соответст вия. М.: Финансы н статистика, 1988. 342 с. 3. Зинчук Н.А. Взаимное преобразование непрерывных и дискретных моделей // Автоматика. 1989. N 1. С.19-31. 4. Ивахненко А.Г. Метод последовательного опробования (перебора) кластеризация - кандидатов по критериям дифференциального типа // Распознавание. Классифнка- ция. Прогноз / Ред. Ю.И.Журавлев (чл.-корр. АН СССР). 1989. N2. С. 126-158. 5. Ивахненко А.Г. Переборные методы самоорганизации моделей и кластеризации: Обзор основных идей // Авто матика. 1989. N 4. С. 82-93. 6. Ивахненко А.Г. Самообучающиеся системы распознава ния и автоматического управления. Киев: Техника. 1969. 39S с. 7. Ивахненко А.Г., Степашко B.C. Помехоустойчивость моделирования. Киев: Наук, думка, 1985. 200 с. 8. Ивахненко А.Г., Чаннская В.А., Ивахненко Н.А. Комби наторный алгоритм МГУА на основе комплексирования прогнозов аналогов // Автоматика. 1990. N 3. С. 10-20. 9. Коэубовский С.Ф., Юрачковскнй Ю.П. Информацион ные критерии селекции моделей // Автоматика. 1981. N 2. С. 80-89. 10. Мюллер И.А. Развитие переборных методов моделиро вания в ГДР // Автоматика. 1989. N 2. С. 18-29. 11. Налимов В.В. Анализ основ экологического прогноза. Человек и биосфера // М.: МГУ. 1985. Вып.8. С. 115-140. 12. Непараметрические модели МГУА. Часть 2 / Ивахнен ко А.Г., Ивахненко Н.А., Костенко Ю.В. н др. // Автома тика. 1989. N 3. С. 3-16. 13. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. М.; Мир, 19S2. 428 с. 14. Стаффорд Е. Кибернетика н управление производст вом. М.: Мир, 1956. 200 с. 15. Степашко B.C. Асимптотические свойства выбора мо делей // Автоматика. 1988. N 6. С. 65-70. |
http://swsys.ru/index.php?id=1307&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Целесообразность применения web-служб в распределенных автоматизированных системах военного назначения
- Эволюционная модель формирования структур виртуальных предприятий
- Система визуализации реального времени на основе программируемых сигнальных процессоров
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике