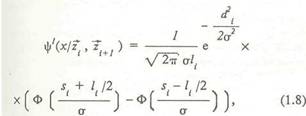Автоматизированная система анализа плоских точечных изображений методом скелетизации как инструмент решения задач прикладной статистики
| Бухштабер В.М () - , Кляцкин В.М. () - , Моттль В.В. () - , Щепин Е.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Методы скелетизации растровых изображений занимают важное место в задачах сегментации и распознавания изображений [2, 5, 18, 25]. Так как понятие скелета распространяется на точечные изображения, мы предлагаем методы и алгоритмы построения скелетов плоских точечных изображений и их программную реализацию. Автоматизированная система анализа плоских точечных изображений (АСАТИ) использует методы скелетизации для решения ряда важных задач прикладной статистики. Среди оригинальных применений системы АСАТИ выделяется скелетизация точечных изображений как средство контрастирования двухмерных проекций многомерных данных в разведочном анализе данных (РАД), значение которого как раздела прикладной статистики все более возрастает. Под скелетом точечного изображения понимается некоторый плоский многосвязный граф. Первый из предлагаемых методов скелетизации является развитием методов главных компонент [17] и главной кривой [26]. Он основан на подходе теории автоматической классификации к описанию массива многомерных данных и является эталоном, в качестве которого используется скелет. Второй метод используется тогда, когда механизм генерации наблюдаемого точечного изображения можно интерпретировать как применение процесса размывания к некоторому скелету. Фактически на этапе РАД методами скелетизации эта гипотеза проверяется на анализируемой выборке, а на этапе подтверждающего анализа скелетизация служит языком информативного описания точечных изображений. Мы рассматриваем две вероятностные модели генерации точечного изображения как совокупности независимых испытаний двухмерной случайной величины, распределение которой определяется скелетом как обобщенным параметром. Такой подход позволяет использовать классические результаты теории вероятностей для конструирования процедур построения скелета и оценки числа его вершин (наш алгоритм основан на методе максимума правдоподобия и критериях х2 [16, 17, 20] и Акаике [10]. Метод скелетизации применяется для решения таких статистических задач, как средство информативного описания в задачах анализа точечных изображений на диаграмме рассеивания и на вероятностной бумаге и при построении статистического портрета динамического процесса; как инструмент автоматизации процесса анализа большого числа изображений в методах целенаправленного проецирования многомерных данных. ОПИСАНИЕ МЕТОДОВ СКЕЛЕТИЗАЦИИ Скелетизация как обобщение метода главных компонент Основное назначение РАД - краткое и точное описание структуры данных. Наиболее наглядным способом описания является визуализация данных, под которой понимается некоторое отображение исходной матрицы данных в двухмерное евклидово пространство, так что исследователь может путем непосредственного визуального анализа этого изображения (например на экране дисплея) подобрать подходящую модель данных. Ниже в качестве модели данных на плоскости рассматривается скелет точечного изображения (ТИ). Под ТИ понимается конечная совокупность точек плоскости Е — {х , к — 1, и}. Термин "скелет изображения" широко используется в теории цифровой обработки растровых изображений [2, 28], однако принятые определения скелета носят геометрический характер и не могут быть непосредственно использованы для анализа ТИ, возникающих в задачах РАД. Всякое непрерывное двухмерное изображение естественно рассматривать как некоторую
плотность распределения на плоскости: высоким значениям плотности соответствует высокое значение эачерненности (яркости). При переходе от непрерывного изображения к растровому, заданному на дискретной сетке, такая'интерпретация изображения полностью сохраняется, поскольку совокупность значений зачер-ненности в отдельных точках растра можно рассматривать как двухмерную гистограмму, отражающую ту же непрерывную плотность. С этой точки зрения точечное изображение отличается от яркостного так же, как выборка из генеральной совокупности отличается от плотности ее распределения. Если рассматривать линию или совокупность линий на плоскости как протяженный "центр" некоторого двухмерного распределения вероятностей, а отдельные точки - как независимые реализации двухмерной случайной величины, определяемой этим распределением, то при таком понимании структуры данных скелет ТИ следует искать как линию, проходящую через явно выраженные сгущения точек. Если моделью носителя данных является линейное многообразие, то задача скелетизации ТИ решается классическим статистическим методом главных компонент. Главная компонента ТИ, которая является прямой, минимизирующей сумму квадратов отклонений точек изображения от нее, называется главной прямой. Иногда в данных объективно присутствует нелинейная структура, т.е. носителем ТИ является некоторое одномерное нелинейное многообразие. В этом случае прямая, получаемая по методу главных компонент, недостаточно объясняет дисперсию точечного множества и поэтому не может служить статистической моделью структуры данного множества. Естественным обобщением метода главных компонент в этом случае может служить метод главной кривой. Под главной кривой в [25] понимается кривая L, минимизирующая остаточную дисперсию точечного множества расстояние от точки *л до кривой L. Здесь d(.,.) -евклидово расстояние. В качестве носителя точек, объясняющего структуру точечного множества Е на плоскости, предлагается использование скелета ТИ [11, 12], что является развитием метода главных компонент и идей построения главной кривой Хасти [26]. Под скелетом L понимается конечный граф ка плоскости, то есть конечное множество точек на плоскости, соединенное регулярными кривыми без пересечений. Скелет ТИ выступает как конечный граф на плоскости, минимизирующий остаточную дисперсию скелетизации. Под остаточной дисперсией скелетизации понимается сумма квадратов расстояний от точек множества до скелета. Расстояние D от точки х до скелета L понимается как расстояние от данной точки до ближайшей точки скелета (1.1). Ограничимся рассмотрением класса кусочно-линейных скелетов, что обусловлено следующими соображениями: - универсальностью как возможностью кусоч но-линейной аппроксимации любой кривой; - универсальностью в смысле возможности представления в кусочно-линейной форме лю бого сложного соответствия двух переменных; - простотой описания и манипулирования ку-
сочно-линеинои моделью и возможностью реализации эффективной вычислительной процедуры; - естественностью данного представления во многих ситуациях (например смеси распределений вида (2.1) на вероятностной бумаге). Формально скелет; L описывается парой (Z,ff), где Z — {T, i = I, m} - множество вершин скелета; HQ{1, .... т}х{1, .... т) - множество пар индексов вершин, связанных ребрами. Алгоритм, разработанный для оценивания положения вершин скелета при фиксированной матрице смежности (эквивалентной множеству Н), реализует процедуру минимизации функционала на множестве допустимых скелетов. Функционал был выбран по аналогии с критерием метода главных компонент, но С учетом более сложной формы носителя точек:
В этом критерии первое слагаемое обеспечивает условие минимизации остаточной дисперсии скелетизации, второе представляет собой штраф на сумму квадратов длин ребер скелета, у — весовой коэффициент частных критериев, представляющий параметр регуляризации алгоритма. Параметр у введен для обеспечения устойчивости процедуры скелетизации и скорости сходимости итерационного процесса (рис.1,2). Отметим, что функционал (1.2) представляет собой типичный функционал автоматической классификации. Оценка положения вершин скелета выводится исходя из условия минимизации данного критерия:
Критерий (1.2) может быть использован и для полной задачи построения скелета, включая и задачу выбора матрицы смежности вершин:
В этом случае алгоритм может состоять из последовательного циклического выполнения двух шагов: — оценивание положения вершин при фиксиро ванной матрице смежности (задача 1.3); - выбор матрицы смежности при фиксирован ном положении вершин:"
Предлагаемый алгоритм решения задачи (1.3) является итерационным. На каждой итерации решается система линейных алгебраических уравнений размерности 2т. Для важного частного случая односвязного скелета без ветвлений (условно названного цепочечным) удалось получить эффективную вычислительную процедуру типа прогонки решения блочно-трехдиагональной системы уравнений. Метод скелетизации, основанный на вероятностной модели точечного изображения Рассмотренный подход к построению скелета ТИ можно назвать аппроксимационным. В качестве критерия аппроксимации данных использована остаточная сумма квадратов отклонений точек от скелета. Такой критерий является оптимальным для визуальной оценки соответствия скелета анализируемому ТИ. В [25] приведено экспериментальное обоснование такого критерия для главной кривой. В рамках вероятностной модели задача построения скелета ТИ рассматривается как задача оценивания обобщенного параметра некоторого распределения вероятностей на плоскости по совокупности наблюдений. При таком подходе скелет трактуется как первичный объект, лежащий в основе порождающей модели изображения. Изображение рассматривается как совокупность независимых реализаций двухмерной случайной величины х, распределение которой f(x/L) определяется скелетом L как обобщенным параметром. С каждой точкой y^L скелета свяжем некоторое параметрическое семейство двухмерных радиальных распределений вероятностей [17] ^(x"jy*jo), например круговое нормальное распределение с математическим ожиданием у и среднеквадратическое отклонение (СКО) о" (в качестве модельного распределения может быть выбрано другое распределение из класса радиальных, в частности равномерное распределение в круге фиксированного радиуса). Пусть на одномерном многообразии, образованном совокупностью линий скелета, определено некоторое распределение вероятностей iji(jj), y^L в предположении, что суммарная длина линий скелета конечна. Со скелетом в целом связывается распределение вероятностей на плоскости f(xjL, <]>(y), а), являющееся непрерывной смесью распределений у(х/у, а) со смешивающим распределением <\>(у). Скелет точечного изображения предполагается как оценка максимального правдоподобия:
где L - априори заданное множество допустимых скелетов, — рассматриваемый класс смешивающих распределений. При итерационном алгоритме построения скелета множество допустимых скелетов L~IL состоит из всех кусочно-линейных графов, имеющих фиксированное суммарное число вершин, равное т. В этом случае скелет L полностью определяется положением своих вершин 7 , .... ~z и матрицей смежности между вершинами. Смешивающее распределение полагается равномерным в пределах каждого прямолинейного отрезка, причем каждый отрезок скелета характеризуется неизвестной смешивающей вероятностью. Метод построения скелета основан на представлении распределения f(xjL) как дискретной смеси распределений, связываемых о каждым прямолинейным отрезком скелета [Т , T..J (без ограничения общности для простоты обозначений предположим, что скелет не имеет вершин с кратностью более двух):роятностеи с такой.плотностью назовем непрерывной смесью нормальных распределений (НСНР). На рис.13 представлены реальные данные, которые можно описать моделью НСНР. Возможна упрощенная форма задания рас пределения, связанного с отрезком либо скеле том в целом — так называемое модифицирован ное нормальное распределение (МНР). Обыч ное круговое нормальное распределение веро ятностей на плоскости полностью определяется выбором центра распределения >> и СКО от. Плотность распределения есть экспоненциаль ная функция от квадрата евклидова расстояния от текущей точки плоскости до центра, нор мированного относительно дисперсии аг-1\~х-у\\2/а2- Плотность МНР определим как экспоненциальную функцию от квадрата евкли дова расстояния от текущей точки плоскости до некоторого отрезка D2(x, [z , z~J) = min\\x-y\\2. Можно показать, что плотность МНР имеет следующий вид:
В формуле (1.8) qt - априорная вероятность распределения, связанного с j-тым отрезком. В качестве распределения, связанного с отрезком /Г Т ), возьмем непрерывную смесь круговых нормальных распределений со смешивающим равномерным распределением вдоль отрезка. Можно показать, что плотность этого распределения имеет следующий вид:
где *,= 1|?ш-?,|| - Длина отрезка (рис.3), с^=|,_ - расстояние от х до прямой, проходящей через данный отрезок, s = \\S.\\ - расстояние от проекции ~хп- точки х на данную прямую до центра отрезка, Ф(х) - функция Лапласа, о- -среднеквадратическое отклонение кругового нормального распределения. Распределение ве- Модели, основанные на плотностях НСНР и МНР, являются достаточно универсальными описателями механизма генерации точечных изображений на вероятностной бумаге (ВБ), диаграмме рассеивания (ДР) и статистическом портрете (СП) некоторого процесса. Алгоритм осуществляет разделение смеси распределений вида (1.8) либо (1.9) по методу максимального правдоподобия [17]. На каждом шаге итерационной процедуры для каждой точки изображения jc вычисляется апостериорная вероятность ее принадлежности к каждому отрезку скелета. Затем, полагая эти апостериорные вероятности константами, алгоритм находит новые значения смешивающих вероятностей и новое расположение вершин, что приводит к решению системы линейных уравнений. Алгоритм особенно эффективен для случая цепочечного скелета. В этом случае каждый шаг итерационного процесса сводится к решению линейной системы векторных уравнений с блочно-трехдиагональной матрицей методом прогонки. Заметим, что в случае графического анализа смеси распределений на вероятностной бумаге искомый скелет представляет собой обычную ломаную на плоскости, что позволяет реализовать эффективную вычислительную процедуру. Во всех случаях неявно предполагалось, что количество вершин скелета m заранее известно; иногда это действительно так, а иногда пользователь сам может задать это число. Но в неко- торых задачах число вершин скелета т само является важным искомым параметром. Для автоматизации процесса оценивания числа т используется критерий, основанный- на понятии сложности скелета. Для выбора сложности скелета т используются информационный критерий Акаике [10] и критерий х [16> 17, 20], для которых последовательно наращивается число ребер скелета. Критерий Акаике состоит в максимизации логарифма функции правдоподобия минус число оцениваемых параметров (вершины скелета и смешивающие вероятности). При использовании критерия х2 тестируется логарифм отношения функций правдоподобия для разного количества вершин скелета. Обозначим через
значение функции правдоподобия при соответствующих оценках параметров q ,..., q z , ..., Решающее правило для оценки сложности скелета при использовании критерия Акаике имеет следующий вид:
При использовании критерия \ в качестве оценки сложности скелета т выбирается такое минимальное число j, для которого справедливо следующее неравенство при выбранном уровне значимости ot:
В методе скелетизации как обобщении метода главных компонент определение сложности (числа вершин) скелета производится на основе анализа последовательности остаточных дисперсий о- „ ст,, ■■■ о-2,,, вычисленных для наилучших аппроксимации ломаной с (-степенями свободы (и ). При этом используется подход, принятый в решении задач автоматической классификации с неизвестным числом классов [14, 17]. Для обоснования этого способа проанализируем поведение ряда остаточных дисперсий в теоретическом случае, когда ТИ генерировано посредством равномерной смеси нормальных распределении вдоль ломаной с к звеньями с заданным параметром а ■ В этом случае типичная последовательность о2., о2, ... О"м ведет себя так: дисперсии а2, при i<2k (число степеней свободы ло-маной} как минимум на порядок превосходят а2, в то время как при n>i>2k величины сгг( имеют тот же порядок, что и ст , т.е. теоретическое значение для и2 равно в этом случае сгг (2n-i)l2rt (поскольку нормированная остаточная дисперсия в данном случае распределена по закону ■% с (2n-i) степенями свободы). Таким образом, при априори известном а число степеней свободы можно определить, вычисляя последовательность о~2 и наращивая / до тех пор, пока не получится неравенство сг <3а. В этом случае именно это / является оценкой сложности. Если же а априори неизвестно, то в качестве критерия останова можно выбрать одновременное выполнение следующих двух неравенств: 2а. <3о\<о\ . В этом случае m — i. Еслн же ни при каком i оба эти неравенства не выполняются одновременно, то вычисляется весь ряд а , с , ... ст м до максимально допустимой сложности М, а потом в качестве оденки сложности берется, например, такое i, при котором максимально отношение сг к среднему арифметическому чисел a ,j>i. В рассматриваемой системе реализованы алгоритмы решения задач скелетизации при наличии априорных линейных ограничений на вершины искомого скелета. Так, некоторые из вершин скелета могут быть заданы априори, а о других может быть известно, что они располагаются на заданных прямых. При наличии линейных ограничений применяется следующее правило для подсчета числа степеней свободы ломаной: число степеней свободы ломаной складывается из степеней свободы ее вершин. При этом фиксированным вершинам приписывается 0 степеней свободы, концевым вершинам и вершинам, расположенным на известных прямых, приписывается одна степень свободы, а всем остальным - по 2 степени свободы. Приписывание концевой вершине только одной степени свободы обосновано тем, что лишь направление конечного ребра влияет на остаточную дисперсию. В частности, для А-звенной ломаной без ограничений данное правило дает 2к степеней свободы. Для того, чтобы сделать процедуру робаст-ной, достаточно применить ее к ряду робаст-ных остаточных дисперсий о2,, а2, .--, ст [17]. В силу итерационного характера алгоритмов скелетизации возникает потребность формирования некоторого начального приближения, причем от качества начального приближения зависят устойчивость и скорость работы алгоритма (рис.5). Робастность итерационных процедур скелетизации обеспечивается наличием встроенной в АСАТИ развитой подсистемы начального оценивания скелета. Начальное приближение для итерационных процедур скелетизации формируется с использованием процедуры "дифференцирования" минимальных остовных деревьев и методов прямолинейного, криволинейного и кусочно-ли-нейного упорядочения точек на плоскости. Под "дифференцированием" минимального остовно-го дерева понимается процесс последовательного усечения его висячих ребер. Критерием
для выбора того или иного исходного приближения является минимум длины ломаной, образованной соединением точек изображения в соответствующем порядке. ПРИМЕНЕНИЕ МЕТОДА СКЕЛЕТИЗАЦИИ НА ЭТАПЕ РАЗВЕДОЧНОГО АНАЛИЗА ДАННЫХ Использование метода скелетизации для графического анализа распределений на вероятностной бумаге Во многих системах анализа данных для проверки гипотезы о виде распределения применяется графический анализ распределений на вероятностной бумаге [1] (например нормальная бумага, логнормальная бумага). Отметим, что ВБ по своей природе является частным случаем ДР, в которой по осям отложены значения эмпирического и теоретического интегральных распределений вероятностей. В случае, когда в качестве теоретического распределения используется некоторая смесь, задачей графического анализа на ВБ является разделение смеси. В качестве примера приведем задачу из области экологии, использующую графический анализ смеси распределений на ВБ [4, 6, 8, 9]. На станциях мониторинга производится регистрация уровней концентрации загрязняющих веществ в атмосфере. К настоящему моменту имеется уже обширная база данных уровней концентраций по ряду регионов страны и по различным типам загрязняющих веществ (двуокись серы, окислы азота, свинец, ртуть и т.д.) [7, 15]. Задача обработки таких данных и выявление фоновых уровней компонент загрязнения атмосферы являются актуальными. Однако сравнивать данные, полученные в разных регионах или в разное время, затруднительно из-за изменчивости данных, связанной с тем, что концентрация загрязняющих веществ определяется совместным воздействием разнообразных физических, метеорологических и географических факторов. В [8, 9] предложена следующая статистическая модель для описания выборки, состоящей из логарифмированных значений уровня концентрации:
где р , р — константы, а — точка переключения действия законов, "размытая" нормальным шумом с дисперсией ет, а Ф(1) — функция распределения нормального закона N(0,1). Предлагаемая модель приближает эмпирические плотности распределения сезонных рядов наблюдений [29]. Предпочтение смеси специального вида (2.1) классической смеси распределений было отдано в связи с особенностями механизма формирования концентраций, заключающегося в раздельном действии факторов (компонент смеси) в различных областях на оси концентраций (с помощью таких смесей удобно описывать процессы типа разладки [13]). Одной из задач статистической обработки данных фонового мониторинга является декомпозиция смеси распределений вида (2.1) с последующей оценкой параметров смеси. В этом случае с помощью метода скелетизации на ТИ можно выделить линейные фрагменты, соответствующие компонентам смеси, дать классификацию наблюдений по ребрам скелета и сформировать оценку параметров смеси. Скелетизация как средство контрастирования структур данных на диаграмме рассеивания Диаграмма рассеивания - одно из наиболее эффективных средств разведочного анализа данных [17, 25, 26], используемых для визуализации зависимостей между переменными в статистике. Парная ДР (в дальнейшем просто ДР) представляет собой ТИ на плоскости двух исследуемых признаков. При исследовании многомерных данных диаграмма рассеивания предстает как визуальная форма представления результатов некоторого отображения исходной матрицы многомерных данных в двухмерное евклидово пространство [17]. Диаграмма рассеивания является одним из наиболее мощных и универсальных средств описания непараметрической связи двух признаков. Отсутствие требования параметризации - основное преимущество ДР. Анализ связей между признаками на ДР заключается в выявлении некоторой регулярной структуры на двухмерном точечном изображении. Программы построения диаграмм рассеивания как средства разведочного анализа данных включены в большинство современных пакетов статистической обработки данных (BMDP, 1MSL, StatGraph, ППСА). На рис.4 представлена упрощенная модель механизма генерации данных на ДР.
Предположим, что для наблюдения доступны два признака (переменные) / и g, формируемые под воздействием некоторого общего доминирующего латентного фактора X и некоторых индивидуальных (мешающих) факторов е и е . Без потери общности для простоты изложения принята аддитивная модель воздействия индивидуальных факторов е; и я на признаки / и g
Таким образом, возникает задача выявления скрытого фактора X, определяющего формирование процессов/и g, посредством анализа ДР. С помощью ДР можно отобразить и провести непараметрический анализ самых сложных видов взаимосвязи переменных / и g - не только взаимосвязи типа /— ty(g) или g = Первая из рассмотренных моделей генерации ТИ может быть легко переформулирована на ДР в терминах предложенной модели (2.2) генерации ТИ. Пусть F(X) и G(X) - некоторые ломаные. Тогда в предположении, что е =0 и е =0, изображение f-g на ДР будет представлять некоторую ломаную L при непрерывном изменении фактора X. Предположим, что латентный фактор X представляет собой одномерную случайную величину, равномерно распределенную вдоль линии L. Положив е и е центрированными нормально распределенными одномерными случайными величинами, получим первую модель генерации ТИ. Для повышения эффективности анализа ДР в интерактивном режиме применяют различные графические дополнения, получаемые посредством обработки ДР различными статистическими методами [17, 25, 26, 29]: - выделение графическими средствами выбро сов (outliers) на изображении [17]; - кодирование уровня концентрации точек (двухмерной плотности распределения) с помо щью специальных графических примитивов — "подсолнечников", число линейных сегментов ("лепестков") которых пропорционально числу точек в различных областях ТИ [26]; - сглаживание (графическое суммирование) (smoothing) ДР - наложение на ДР некоторой средней линии ТИ. Кливленд [25, 26] предло жил несколько алгоритмов сглаживания ТИ: среднее, верхнее и нижнее, сглаживание двух мерных распределений с помощью пары сред них сглаживаний, сглаживание шкалы отноше ний и полярное. Алгоритм среднего сглаживания ДР. Пусть имеется ТИ E — {z—(x. у), /=/,«} на ДР признаков X и У. Алгоритм состоит из следующей последовательности шагов: а) выбирается некоторое число 0 б) для каждой точки z определяется q ближай ших к ней по оси х точек Е, затем через эти q точек методом взвешенных наименьших квад ратов проводится кривая y — g^x). Вес точек подбирается так, чтобы наибольший вес имели ближайшие к точке z no оси X точки; в) вычисляется величина У,=8/х.)1 г) вычисляются остатки г = у —у. и вес точек, возрастающий с уменьшением остатков; д) шаги б) и в) повторяются, но в качестве ве сов используются произведения весов, вычис ленных на шагах б) и г). Последние два шага служат для придания процедуре свойств робасткости. Все способы предназначены для контрастирования структуры представленных на ДР данных и, следовательно, для облегчения последующей содержательной интерпретации взаимосвязи признаков на ДР. Нами предлагается метод скелетизацяи ТИ [11, 12] для информативного описания ДР, поскольку скелет (остов, срединная линия) - достаточно естественный и вместе с тем универсальный язык, в терминах которого удобно описывать структуру данных на ТИ. Скелет ТИ - графическое дополнение ДР, сходное с линией сглаживания Кливленда. Предпочтение методам скелетнзации отдается по следующим соображениям: - с помощью скелета можно описывать соот ветствия признаков любой степени сложности (многосвязные, разветвляющиеся, замкнутые кривые), а с помощью линии сглаживания - лишь соответствия типа функциональной зави симости либо простого цикла; - управляя степенью сложности скелета, мож но синтезировать экономное, сжатое описание структуры ДР (линия сглаживания Кливленда имеет сложность, равную сложности исходного множества точек); - реализованы эффективные численные процедуры построения цепочечных скелетов. Благодаря применению ДР были получены важные результаты в некоторых статистических задачах геофизики. 1. Анализ взаимосвязи двух природных про цессов - индекса активности зеленой биомассы и концентрации СО; в атмосфере и выявление скрытого доминирующего фактора, определяю щего формирование обоих процессов [29]. 2. Определение степени соответствия мате матической модели углеродного цикла реаль ным измерениям концентрации СО на станци ях мониторинга [27]. 3. Проверка гипотезы связи роста концент рации атмосферного СО с ростом эмиссии СО за счет сжигания топлива [27]. 4. Задача синхронизации двух процессов при условии справедливости гипотезы, что су ществует некоторый скрытый фактор, влияю щий на формирование обоих процессов с некоторым фазовым сдвигом. Все эти задачи могут быть решены с использованием диаграммы рассеивания с наложенным на нее скелетом ТИ. Скелет как язык описания статистического портрета процессов Статистический портрет представляет собой более общее понятие по отношению к диаграмме рассеивания. Когда говорят о ДР, предполагается, что зафиксированы оси координат, в которых формируется ТИ. Идеология построения СП процесса не зависит от привязки к конкретной системе координат и заключается а поиске общих закономерностей в исследуемом процессе путем наложения большого числа его реализаций на одно ТИ и поиска мест сгущения точек на изображении (которые соответствуют общим чертам в различных реализациях исследуемого процесса в отличие от разреженных областей, характеризующих индивидуальные особенности отдельных реализаций). В частности, при решении задачи прослеживания динамики взаимосвязи между двумя характеристиками возникает двухкомпонентный процесс - динамическая ДР, - реализациями которого являются мгновенные ДР. Статистический портрет искомой динамики взаимосвязи получается путем наложения большого числа мгновенных ДР на одно ТИ. Классическим примером применения метода СП может служить метод Бокажа анализа рентгеновских томограмм [21]. Скелетизация ТИ — один из способов информативного описания СП исследуемого динамического процесса, так как скелет выделяет распределение двухмерной плотности данного процесса. Скелетизация как инструмент целенаправленного проецирования многомерных данных Целенаправленное проецирование (ЦП) -один из наиболее современных методов разведочного анализа данных, состоящий в снижении размерности многомерных данных посредством поиска их информативных линейных проекций в пространстве малых размерностей. Скелетизация ТИ в сочетании с многооконными и динамическими формами диаграммы рассеивания [17] может служить хорошим дополнением к традиционным методам ЦП. Рассмотрим задачу поиска наиболее выразительных двухмерных проекций многомерных данных. Примем в качестве критерия выразительности двухмерной проекции качество ее скелетизации, под которым будем понимать остаточную дисперсию скелетизации (при фиксированном допустимом классе скелетов). В [3, 17] алгоритм поиска наиболее выразительной проекции описан как процедура оптимизации некоторого критерия (проекционного индекса) на многообразии возможных направлений проецирования. Применив этот алгоритм для критерия остаточной дисперсии скелетизации, получаем возможность решать задачи РАД для МД, модель структуры которых определяется набором пересекающихся гиперплоскостей в исходном пространстве. Так достигается высокая степень наглядности и автоматизации процесса поиска наилучшей двухмерной проекции, что особенно важно в интерактивных графических системах анализа данных. Описание автоматизированной системы анализа точечных изображений АСАТИ предназначена для интерактивного графического анализа взаимосвязей между характеристиками климатических систем, в том числе для информативного описания непараметрической связи между характеристиками климатических систем на парной диаграмме рассеивания характеристик [22-26, 29] (задача 1) и для анализа точечных изображений на вероятностной бумаге, возникающих при построении статистической модели загрязнения атмосферы [4, 6-9, 19] (задача 2). В АСАТИ используются следующие алгоритмы анализа данных: - алгоритмы предварительной обработки данных, в том числе: алгоритм построения гистограмм, алгоритм преобразования данных на вероятностную бумагу, алгоритм построения изображения на ДР, алгоритмы вычитания тренда из данных, четыре алгоритма фильтрации ТИ (с использовани-
ем анализа минимальных остовных деревьев; с использованием метрики "ближайшего соседа"; по критерию минимума концентрации; по критерию изолированности); - алгоритмы скелетизации; — алгоритмы классификации наблюдений по компонентам смеси и оценки параметроз сме си; - алгоритмы визуализации многомерных дан ных в виде графиков, гистограмм, данных на вероятностной бумаге и на диаграмме рассеи вания и внешних/внутренних (оболочки/скеле ты) описаний двухмерных изображений; — алгоритмы графического редактирования изо бражений. ППП реализован на ЭВМ типа PC/AT (ми нимальная конфигурация - процессор IN- TEL-286, терминал EGA) на языке FORTRAN MicroSoft версии 5.0 (базовые процедуры взаимодействия с драйвером "мыши" написаны на ассемблере). В качестве базовой графической библиотеки использовалась библиотека GRAPHICS фирмы MicroSoft. Пакет состоит из более чем 80 модулей. Описание сценария функционирования АСАТИ Приведем пример функционирования АСАТИ в режиме решения задачи 2. На рис 6. представлен типичный отрезок временного ряда измерений концентраций сернистого газа на станции фонового мониторинга Березина (1983 г., теплый сезон). Рис. 7 представляет преобразование данных на вероятностной бумаге. Рис. 8 иллюстрирует процесс удаления из данных линейного тренда. На рис. 9 представлен процесс классификации наблюдений по компонентам смеси и анализа окрестностей точек переключения частных законов с использованием критерия отношения собственных чисел. На рис. 10 приводятся итоги анализа смеси распределений на ВБ. На следующих трех рисунках представлен процесс решения задачи анализа диаграммы рассеивания с помощью системы АСАТИ. На рис. 11 и 12 изображены отрезки временных рядов измерений концентраций углекислого газа на Гавайях и Южном полюсе, а рис. 13 представляет парную диаграмму рассеивания этих данных. Список литературы 1. Айвазян С,А., Енюков И.С., Мешалкнн ЛЛ. Прикладная статистика. Исследование за в иен мосте й, М.: Финансы и статистика, 1985, 2. Борисенко В.И., Златопольский А.Л„ Мучник И.Б. Сегментация изображения (состояние проблемы)//Автоматика и телемеханика. - М.; АН СССР. Вып. 7. 19S7. С. 3-56. 3. Бучштабер В.М., Енюков И.С. Методы и алгоритмы це ленаправленного проецирования в разведывательном анализе многомерных данных // Многомерный статистический анализ и вероят ностное моделирование реальных процессов / Под. ред. СА. Айвазяна, СЕ. Кузнецова. - М.; Наука, 1990. С. 16-30. 4. Букшгабср Б.М., Зеленюк Е.А., Зубенко А.А. Конструирование ннтеракгнвних систем анализа дакнык. Мг: Финансы и статистика, 1989. 5. Грановская P.M., Березная И.Я. Целостное представление формы ь виде скелета // Сб.: Проблемы бионики. - Харьков: Изд. ХГУ, 1983. Внп. 30. С. 30-25. 6. Зеленюк Н.А. Построение и исследование статистической модели фонового загрязнения атмосферы: Автореф. дне. ... канд. фнз.-мат. наук: ОТК 519.2S4:502.5/203/ М.:1986. 22 о. 7. Израэль Ю.А. Экология и контроль состояния природной среды. М.: Гидромстеоиздат. Моск. отд-ние. 1984. 8. К проблеме выявления и оценки фоновых уровней компонент загрязнения атмосферы / Ю.А. Израэль, М.Я. Антоновский, В-М. Бучш- тэбер, Е.А. Зеленюк // ДАН. М, 19S7. Т.292. N 2. 9. К статистическому обоснованию компонент регионального загряз нения атмосферы в фоновом районе / Ю.А. Израэль, Ф.Я. Ровинский, М.Я. Антоновский и др. // ДАН. М., 1984. Т.276. N 2. 10. Кашьяп Р.Л., Рао А.Р. Построение динамических стохастических моделей по экспериментальным данным. М.: Наука, 1*77. И. Кляцкин В.М„ Моттль В.В., Щепин Е.В. Статистический подход к скелетизации точечный изображений // Комбинаторно-статистически* кдегоды анализа н обработки информации, экспертное оценивание: 3-ий Всесоюз. шк.-семинар, Одесса, 10-15 октябре 1990 г. Одесса, 1990. С 75-7п. 12. Кляцкнн В.М, Моттль В.В., Щепнн Е.В. Статистический подход к скелетнзации точечных изображений // Обработка изображений и дистанционное зондирование ОИДИ-90: Междунар. конф-, Новосибирск, 19--21 августа 1990 г, Новосибирск, 1990. С. 1М-1М. 13. Колмогоров А.П., Прохоров Ю.В., Ширяев А.Н. Вероят- ностностатистические методы обнаружения спонтанно возникающих эффектов // Тр./Мат. нн-т им. В.А. Стеклова. CLXXXII. Теория вероятностей, теория функций, механика; Сб. ст. - М.: Наука, 1988. 14. Методы анализа данных / Под ред. Э. Дидэ / Пер. с франц.; Под ред. СА. Айвазяна, В.М. Бухштабсра. - М.: Финансы и статистика, 1985. 356 с. 15. Осзор состояния окружающей природы в СССР / Под ред. Ю.А. Израэля, Ф.Я. Ровинского. - М.: Гидрометеоиздат. Моск. отд-ние. 1990. 114 с. 16. Орлов А,И. Некоторые вероятностные вопросы теории клас сификации // Прикладная статистика. М.; Наука, 1983. С. 166-179. 17. Прикладная статистика. Классификация и снижение размерности I СА. Айвазян, В.М. Буяштабер, И.С. Енюков, Л.Д. Мешалкин. - М.: Финансы и статистика, 1989. 18. Садыков С,С, Самандров И.Р. Скелетнзацня бинарных изображений // Зарубежная радиоэлектроника, М.: Радио и связь. Вып. 11, 1985. С. 30-35. 19. СВИС для распознавания образов и обработки изображений / Под. ред. К. Фу / Пер. с англ.; Под ред. В.А, Абрамова. - М.; Мир, 19S8. MS с. 20. Уилкс с. Математическая статистика / Пер. с англ. - М.: Наука, 1967. 633 с. 21- Харман Г. Восстановление изображения по проекциям. Основы реконструктивной томографии многомерных данных. М.: Мир, 1983. 349 с. 22. Antonovski M.Ya, Buchslabcr V.M. and Zubenko A.A., 1988. Statistical Analysis of Long-Ttrm Trends [n Atmospheric CO Concentration at Baseline Stations. WP-BS-122. International Institute Tor Applied Systems Analysis, Laxenburg, Austria. 23. Antonovski M.Ya, Buchstaber V.M. and Zubenko A.A- 1989. Exploratory analysis of trends In the series of concentrations of CO in almosphere. In Problems of Ecological Monitoring and Ecosystem Modeling, Volume XII, Hidromcteotedat, Leningrad. 24. Antonovskl M.Ya, liuchslaoer V.M., 1989, Exploratory analysis of tendency in CO concentration data In the atmosphere. Third international conference on analysis and evaluation of atmospheric CO data, present and past, Hirterzarten, 16-20, October, 1989, WMO. 25. Cleveland WS. and McOIII R. The Many Faces of a scatterplot // Journal of the American Statistical Association, December 1984, Volume 1% N 388, Theory and Methods Section. 26. Cleveland VJS. ind McOill R. Graphical Perception Theory, Experimentation and Application to the Development of Graphical Methods // Journal of the American Statistical Association, September 1984, Volume 79, N 387, Application Section. 27. CD1C Numeric data collection Atmospheric CO Concentration, The NOAA/GMCC, Flask and Continuous. Sampling Network, September 1984, NDP-005. 28. Serra J. Image analysis and mathematical morphology. N.Y.:Acad. Press. 1981. 29. Tucker CJ, Fung I.Y., Keeling C.D. and Gammon R.H. Relationship between atmospheric CO variations and a satellite-de rived vegetation Index // Nature international weekly Journal of science, Volume 319, N 6050 16-22 January 1986. |
http://swsys.ru/index.php?id=1337&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics: