Программные продукты и системы

Среди множества задач, возникающих при анализе трафика в корпоративных компьютерных сетях, весьма важной является задача прогнозирования возникновения критических ситуаций в функционировании сети, связанных с ограниченной пропускной способностью отдельных ее элементов. Для решения указанной задачи прогнозирования (в первую очередь долгосрочного) предлагается использовать математический аппарат статистики экстремальных значений.

Как известно, статистика экстремальных значений представляет собой определенную ветвь классической математической статистики, достаточно интенсивно развивавшуюся в 50–60-е годы прошлого века. В наиболее законченной форме ее основные теоретические результаты нашли свое отражение в монографии [1].

Только сравнительно недавно интерес к статистике экстремальных значений снова возрос, в первую очередь в прикладном плане. Появились интересные публикации отечественных авторов, в которых наглядно демонстрируются ее возможности для получения новых важных результатов в различных предметных областях.

В качестве характерных примеров можно указать такие области, как гидрология [2,3], анализ сейсмоопасности и сейсмостойкости [4] в материаловедении и строительстве [5].

Представляется достаточно перспективной возможность использования данного подхода и для анализа трафика в компьютерных сетях.

Как отмечалось еще Э. Гумбелем, использование статистики экстремальных значений наиболее продуктивно при выполнении следующих двух условий.

1.   Наблюдаемый процесс обладает свойством цикличности, то есть определенной повторяемостью своего поведения через некоторый фиксированный интервал времени (интервал цикличности); желательно также, чтобы этот интервал задавался естественным путем, определяясь самой природой процесса, а не вводился искусственно. В частности, в гидротехнике, метеорологии этот интервал цикличности равен одному году.

2.   Наибольший интерес с точки зрения исследователя (пользователя) представляют именно экстремальные значения, имеющие место в каждом цикле, поскольку они могут привести к серьезным последствиям, скачкообразно возрастающим потерям и т.п. (прорыв дамбы или плотины с последующим катастрофическим наводнением, обрушение зданий и др.).

Такого рода ситуация имеет место, когда речь идет о трафике, контролируемом в различных точках компьютерной сети. В данном случае интервал естественной цикличности равен одним суткам.

Математические основы метода анализа данных с использованием статистики экстремальных значений. Метод базируется на предварительном получении информации о значениях наблюдаемой случайно изменяющейся переменной X в течение N циклов повторяемости. Применительно к анализу интенсивности трафика это могут быть, например, ежесуточные наблюдения общей длительностью N суток. Пусть каждая из отдельных реализаций содержит L наблюдений xln (l=1,2,…,L; n=1,2,…,N). Зафиксируем для каждой реализации максимальное значение Xn и образуем новую выборку, содержащую N максимальных значений. Если N не слишком мало, можно использовать некоторые общие асимптотические результаты.

Известно, что существует всего три типа асимптотических распределений для рассматриваемых максимальных значений. Можно показать, что для рассматриваемых величин xln имеет место экспоненциальный характер затухания соответствующих функций плотности. Асимптотической функцией распределения вероятностей экстремальных значений для этого случая является так называемое первое предельное распределение, или распределение Гумбеля: . Здесь a и u – соответственно параметры формы и положения кривой интегральной функции распределения вероятностей.

Эмпирический анализ экстремальных значений и формирование различного рода заключений обычно проводятся с помощью так называемой вероятностной бумаги [1]. На этой бумаге наблюдаемые значения Xn, размещенные в порядке возрастания в точках, соответствующих ординатам , будут лежать с некоторым разбросом около прямой линии , где  – приведенная переменная. Для распределения Гумбеля .

Пусть имеется выборка из N экстремальных значений. Упорядочим их в порядке возрастания (неубывания) значений, то есть образуем вариационный ряд, состоящий из элементов X(j), j=1,2,…,N. Зафиксируем положение каждой из точек (pj , X(j)), где , на плоскости (X, y). Если экстремальные значения подчиняются распределению Гумбеля, то все они с некоторыми отклонениями должны располагаться вблизи некоторой прямой.

Шаблон для нанесения точек вариационного ряда с координатной сеткой, где в качестве одной из координат используются значения самой наблюдаемой случайной величины X, а в качестве другой – приведенная переменная y, и принято называть вероятностной бумагой. В большинстве случаев наряду с приведенной переменной или даже вместо нее указываются и соответствующие вероятности p, но уже, конечно, в нелинейном масштабе. В верхней части шаблона размещается еще одна нелинейная шкала – шкала периода повторяемости T.

Период повторяемости вводится с помощью соотношения:

.                (1)

Он показывает, через какой промежуток времени в среднем будет наблюдаться событие, заключающееся в превышении фиксированного уровня x. При этом единицей измерения времени является интервал цикличности наблюдаемого процесса.

Анализ трафика с использованием статистики экстремальных значений. Изложение для наглядности будет вестись на модельном примере.

Моделировался трафик, представляющий собой пуассоновский поток с интенсивностью 3,8*107 бит/сек. Фиксировались усредненные за 1 минуту значения трафика. Интервал цикличности составлял одни условные сутки, в течение которых фиксировалось L значений интенсивности: L=1440. Общая длительность эксперимента – 30 дней (N=30).

Для каждой суточной реализации найдены максимальные значения Xn. Соответствующие экспериментальные точки описываются распределением Гумбеля:

.                         (2)

Из (2) следует, что оценками параметров положения и масштаба являются: ; . Рассмотрим более конкретно результаты по анализу и прогнозированию трафика, которые могут быть получены с помощью статистики экстремальных значений.

Анализ и прогнозирование событий, связанных с превышением заданного уровня интенсивности трафика. Имеется в виду получение информации о средней длительности интервалов между превышениями фиксированного уровня интенсивности трафика. Такая информация получается очень просто: пользователь задается некоторым интересующим его уровнем интенсивности и для точки, соответствующей этому уровню, находит по оси абсцисс искомое значение периода повторяемости T.

Если, например, пользователя интересует уровень 3,4*108 бит/сек., можно прогнозировать, что он будет превышаться в среднем примерно 1 раз в 7 суток. Аналогичным образом для уровня B (интенсивность 3,4*108 бит/сек.) получим =91, то есть превышение данного уровня будет происходить примерно 1 раз в 3 месяца.

Если первый результат носит справочный характер, так как выбранный уровень уже неоднократно превышался ранее, второй результат может иметь существенное прогностическое значение. Если, например, уровень B соответствует предельной пропускной способности данного элемента компьютерной сети, то можно оценить частоту появления сбоев, связанных с его перегрузкой.

Рассмотрение может быть дополнено интервальным анализом. Граничные значения можно использовать в качестве пессимистической  (верхняя граница) и оптимистической  (нижняя граница) оценок интервала повторяемости T. Для рассмотренных двух уровней получим соответственно = 5, = 16 и = 28, = 258.

Прогнозирование последствий увеличения интенсивности трафика. Очевидно, что при увеличении интенсивности трафика значения периодов повторяемости будут уменьшаться. На практике важно количественно оценить, насколько сильным будет уменьшение. Для ответа на этот вопрос найдем зависимость интервала повторяемости  от коэффициента увеличения интенсивности трафика k для некоторого уровня интенсивности трафика C.

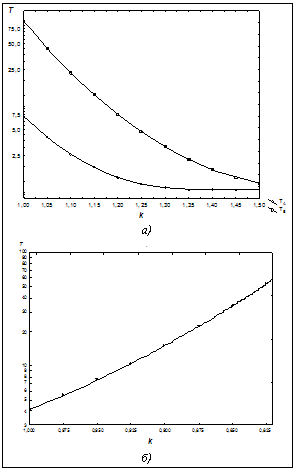
На рисунке  в части а) представлены найденные с помощью (1), (2) зависимости периода повторяемости  от коэффициента k для двух уровней: C=А и C=B. Очевидно, что даже относительно небольшое увеличение трафика приводит к существенному уменьшению интервала повторяемости.

Анализ перегруженной сети. Рассматривается ситуация, когда интенсивность трафика, проходящего через анализируемый элемент сети, настолько велика, что достаточно часто имеет место его перегрузка, то есть достижение уровня предельно допустимой пропускной способности. В этом случае важно оценить возможности исправления такого положения.

Будем считать, что уровень предельной пропускной способности анализируемого элемента сети составляет величину 3,2*108 бит/сек. Предельному уровню =3,2*108 бит/сек. будет соответствовать период повторяемости T=4,1 единицы интервала цикличности. Это значение может оказаться неприемлемым с точки зрения пользователей, и тогда возникнет задача увеличения периода T. Этого можно добиться путем определенного снижения интенсивности трафика в k раз за счет переключения части пользователей на другие маршруты сетевой структуры.

Можно найти достаточно простую формулу, отражающую зависимость интервала повторяемости T от коэффициента k для перегруженного трафика. На рисунке в части б) представлена соответствующая зависимость. Если задаться желательным значением интервала повторяемости, то с помощью данного графика можно найти соответствующий коэффициент необходимого уменьшения трафика k. Отметим, что даже относительно небольшое снижение интенсивности может существенно увеличить интервал повторяемости.

Предложенный подход при всей своей относительной простоте может оказаться полезным при долгосрочном прогнозировании поведения компьютерных сетей.

Список литературы

1.   Гумбель Э. Статистика экстремальных значений./ Пер. с англ. – М.: Изд-во МИР, 1965.

2.   Писаренко В.Ф., Болгов М.В., Осипова Н.В., Рукавишникова Т.А. Применение теории экстремальных событий в задачах аппроксимации распределений вероятностей максимальных расходов воды. // Вопросы инженерной гидрологии. – Вып. 180. – Л.: Гидрометеоиздат, 1970.

3.   Найденов В.И., Кожевникова И.А. Почему так часто происходят наводнения? // Природа. – 2003. – № 9.

4.    Embrechts P., Kluppelberg C., Mikossch T.// Modellingextreme events for insuranceand finance. / Berlin, 1997.

5.   Нерсесов И.Л., Сыдыков А., Нурмагамбетов А., Михайлова Н.Н. Сейсмический режим Северного Тянь-Шаня…// Физика Земли. – 1981. – № 5.