Моделирование и верификация программ как элемент контролируемого выполнения
| Галатенко В.А. (galat@niisi.msk.ru) - НИИСИ РАН, г. Москва (зав. сектором автоматизации программирования), г. Москва, Россия, кандидат физико-математических наук, Костюхин К.А. (kost@niisi.msk.ru) - Научно-исследовательский институт системных исследований РАН (НИИСИ РАН) (старший научный сотрудник), Москва, Россия, кандидат физико-математических наук, Малиновский А.С.;Шмырев Н.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Использование модели дает возможность не только контролировать работу приложения, но и доказывать некоторые его свойства, такие как корректность указателей, отсутствие блокировок или планируемость. Высокоуровневое описание приложения в распределенной системе позволяет эффективно организовать управление системой, локализовать ошибку или наглядно отобразить состояние работоспособности системы. Подобные возможности критичны для полной реализации концепции контролируемого выполнения распределенных систем. Наиболее трудная задача – выбор формализма для описания приложения. В настоящее время предложены различные способы описания работы распределенного приложения – конечные автоматы, сети Петри, исчисления предикатов со временем и ряд других. Свойства модели могут проверяться быстрым алгоритмом, однако зачастую выразительности модели не хватает для описания даже простейших распределенных приложений, тем более тех, в которых нужно учитывать требования по ресурсам, причем не только время выполнения задач и планируемость – на приложения часто накладываются ограничения по используемой памяти или загрузке сети. Моделирование приложений В качестве примера формализма, широко применяемого в моделировании систем реального времени, в том числе систем управления физическими объектами, можно рассмотреть гибридные автоматы, как правило, описываемые с помощью пакета HyTech [1]. Гибридный автомат состоит из набора состояний с условиями на некоторые переменные, обычно соответствующие физическим величинам (время, количество и т.д.). Для каждого состояния определены скорости изменения переменных и границы, при которых происходит переход. Такое описание позволяет не только доказать утверждения о том, что исследуемая характеристика не превышает некоторого значения, но и получить значения параметров, при которых работа автомата будет корректной. Например, рассмотрим описание гибридного автомата для описания работы цистерны с водой: var x: clock; y: analog; automaton water synclabs:; initially on_0 & y=1; loc on_0: while y<=10 wait {dy=1} when y=10 do {x' = 0} goto on_1;
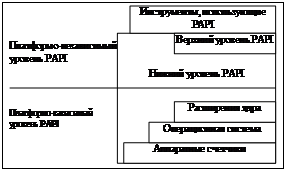
loc on_1: while x<=2 wait {dy=1} when x=2 goto off_0; loc off_0: while y>=5 wait {dy=-2} when y=5 do {x' = 0} goto off_1; loc off_1: while x<=2 wait {dy=-2} when x=2 goto on_0; end Переменная x отражает время, а y – уровень воды в цистерне. В зависимости от уровня воды открываются и закрываются заслонки, и он изменяется. Используя описание, можно доказать, что уровень воды не превысит критического значения. Несмотря на то, что гибридные автоматы позволяют удобно описывать класс систем управления, применение их на практике затруднительно [2]. Накопление вычислительной ошибки усложняет применение доказанных утверждений. Создание исходного кода, соответствующего автомату, – также достаточно непростая задача. Другой подход к решению исходной задачи можно продемонстрировать на примере Blast [3]. Используя механизмы отложенной абстракции для доказательства утверждений о достижимости заданной метки в исходном коде на языке Си, Blast позволяет доказывать утверждения о корректности приложения, отслеживать принадлежность переменных интервалу или проверять наличие блокировок в коде. Строя простейшую модель приложения и в дальнейшем уточняя ее для доказательства достижимости метки в исходном коде, Blast позволяет также получить схему вызовов, приведших к ошибочной ситуации, и может использоваться для создания автоматических тестов. Например, для функции int foo(int x, int y) { if(x>y) { x=y-x; assert(x>0); } } Blast позволяет не только доказать невыполнимость утверждения x>0, но и определить последовательность вызовов функций, приводящую к нештатной ситуации: Size:5 4 :: 4: Pred(x@foo>y@foo) :: 5 5 :: 5: Block(x@foo = y@foo - x@foo;) :: 6 6 :: 6: Pred(Not (x@foo>0)) :: 6 6 :: 6: FunctionCall(__assert("foo.c",6,"x>0")) :: -1 К сожалению, не всякое утверждение может быть легко выведено из исходного кода. Так, в представленном далее примере утверждение x==y приходится проверять во время выполнения приложения. Подобные дополнительные утверждения, проверяемые на стадии выполнения, позволяют значительно расширить класс доказанных утверждений. Рассмотрим метод из [4], который применяется для проверки корректности указателей: void main ( ) { int x = 0, y = 0; while (foo( )) { x++;y++; } runtime_assert (x == y); while (x > 0) if (x!=y) { x--; y--; } assert (y= =0); } Исходное приложение оснащается проверками указателей, причем некоторые из них выполняются с помощью Blast. Такие проверки отбрасываются, позволяя оптимально, без введения дополнительных затрат инструментовать приложение для проверки указателей. Вместе с тем Blast имеет и серьезный недостаток – современные алгоритмы отложенной абстракции неэффективны при проверке распределенных приложений. С помощью механизмов доказательства достижимости метки сложно описать взаимодействие распределенных процессов. Более того, полученные модели обладают слишком большим числом состояний и проверяются неэффективно. Наилучшим, по мнению авторов, подходом, комбинирующим механизмы для описания моделей и их связи с исходным кодом, является подход, выбранный создателем инструмента MAGIC [5]. Используется модель на основе системы с отмеченными переходами (Labelled Transition System, LTS), позволяющая описывать конечные автоматы. Важно, что описанная модель может проверяться не только на наличие некоторых свойств (достижимости), но и на соответствие исходному коду с помощью отложенной абстракции. Приведем фрагмент кода, описывающий вычисление с условиями в терминах LTS: int my_proc(int x) { int y; if(x==0) { y=foo(); if (y= =0) return 10; else return 20; } } cprog my_prog=my_proc { abstract abs_5, {($1= =0)}, S1; } cproc my_proc { abstract { abs_1 , ($1 == 0) , S1 }; } S1=(call_foo->S2), S2=(return {$0==10}->STOP | return {$0==20}->STOP). MAGIC позволяет описывать распределенные системы и применяется для проверки корректности таких приложений, как, например, совместное взаимодействие клиента и сервера по протоколу SSL [6]. Применение MAGIC для описания ресурсов системы, в том числе систем реального времени, требует дополнительных модификаций. Важным компонентом подобной системы должен стать высокоточный инструмент измерения времени и производитель- ности. PAPI-интерфейс средств профилирования Современные процессоры из семейств x86, IA-64, Power, MIPS и др. поддерживают профилирование приложений посредством использования аппаратных счетчиков – специальных регистров, фиксирующих аппаратные события определенного типа. В качестве примера аппаратных событий можно привести общее число процессорных тактов и выполненных команд, число выполненных операций с плавающей точкой, число промахов при обращении к виртуальной и кэш-памяти, а также ряд других. Целью проекта PAPI – Perfomance Application Programming Interface (http://icl.cs.utk.edu/projects/ papi/) являются разработка, стандартизация и реализация переносимого и эффективного прикладного программного интерфейса для доступа к аппаратным счетчикам. Проект PAPI поддерживается консорциумом Parallel Tools Consortium (http://www.ptools. org) и является стандартом для разработчиков программного обеспечения, осуществляющего профилирование кода. В PAPI выделяются два основных уровня: платформо-независимый и платформо-зависимый, скрывающий от пользователя детали реализации доступа к аппаратным счетчикам конкретного процессора. Для этого функции PAPI на платформо-зависимом уровне могут использовать расширения ядра, функции целевой операционной системы или непосредственно язык ассемблера. На рисунке представлена архитектура PAPI. В проекте PAPI впервые предложено стандартизованное переносимое решение для профилирования кода посредством управления аппаратными счетчиками событий. Существуют реализации PAPI в виде библиотек для многих современных платформ. Следует отметить также хорошую документированность проекта и простоту использования предлагаемых интерфейсов. На основе библиотеки PAPI в рамках инструментального комплекса СОМ создана библиотека профилирования. Функции этой библиотеки ориентированы на получение информации о времени выполнения отдельных участков кода прикладных программ программируемых процессоров сигналов, а также потоков операционной системы реального времени, выполняющейся на MIPS-совместимых процессорах. Программируемый процессор сигналов представляет собой многопроцессорную ЭВМ, состоящую из отдельных плат – модулей обработки сигналов. На каждом из модулей располагаются 4 или 8 процессоров цифровой обработки сигналов, имеющих как локальную память, так и память, разделяемую с остальными процессорами модуля. Собранная информация может затем обрабатываться независимыми программами-профилировщиками. MAGIC с ресурсами Эффективным способом создания надежной системы поддержки и разработки приложений является расширение инструментального комплекса MAGIC для работы с системами, потребляющими ресурсы. Этот комплекс не только позволяет доказывать свойства планируемости, но и предоставляет возможность использования полученных моделей для проверки корректности выполнения приложений. Большая часть компонентов, необходимых для реализации комплекса, уже описана. С помощью библиотеки PAPI можно точно измерить время, затраченное на выполнение переходов. Описание стандартных вызовов функций выделения памяти позволяет контролировать расход динамической памяти в приложении. Простое расширение синтаксиса MAGIC дает возможность учитывать потребление некоторого ресурса в системе с переходами: S1=(call_foo->S2, +10), S2=(return{$0==10}->STOP, -20| return{$0==20}->STOP, +30). Для каждого состояния задаются не только условия переходов, но и затраты ресурса на его выполнение, например, расход памяти после обработки запроса, поступившего к приложению.
К сожалению, не все примитивы, используемые в системах реального времени, просто описываются в терминах LTS. Легко покрывается только класс систем, взаимодействующих с помощью синхронных сообщений. Тем не менее, этот класс достаточно широк для описания большого спектра распределенных приложений. Однако следует учитывать, что значительное усложнение модели может сделать недостижимым доказательство утверждений о ее свойствах. Оптимизация работы приложений, выполняющихся под управлением систем реального времени, является трудной и актуальной задачей. Для верификации поведения систем существует достаточное количество средств моделирования. Различные варианты использования высокоуровневых моделей при контролируемом выполнении программ, рассмотренные выше, позволяют с разной степенью точности представлять приложение, контролировать соответствие приложения составленной модели. Важной работой, которую еще предстоит выполнить, является использование построенных моделей в различных компонентах отладочного комплекса. Кроме традиционных проверок на корректность указателей и генерации тестов, перспективным направлением исследований является визуализация производительности программы с помощью модели, использование сигнатур ошибок, взаимодействие со средствами мониторинга. Список литературы 1. Henzinger T.A., Ho P., Wong-Toi H. HyTech: the next generation. In Proc. TACAS'95, LNCS 1019, pp. 41–71, 1995. 2. Anand Madhukar, Kim Jesung, Lee Insup. Code Generation from Hybrid Systems Models for Distributed Embedded Systems. In Proc. ISORC'05, pp. 28–36, 2005. 3. Beyer D., Henzinger T.A., Jhala Ranjit, Majumdar Rupak. The Software Model Checker BLAST: Applications to Software Engineering. Int. Journal on Software Tools for Technology Transfer, 2007. 4. Beyer Dirk, Henzinger Thomas A., Jhala Ranjit, Majumdar Rupak. Checking Memory Safety with BLAST, In. Proc. FASE'05, 2005. 5. Chaki Sagar, Clarke Edmund, Groce Alex, Jha Somesh, Veith Helmut. Modular Verification of Software Components in C, Transactions on Software Engineering (TSE), Vol. 30, Nb. 6, pp. 388–402, 2004. 6. Chaki Sagar, Clarke Edmund, Groce Alex, Ouaknine Joel, Strichman Ofer, Yorav Karen. Efficient Verification of Sequential and Concurrent C Programs, Formal Methods in System Design (FMSD), Vol. 25, pp. 129–166, 2004. |
http://swsys.ru/index.php?id=1603&lang=.&page=article |
|
| Статья находится в категориях: Моделирование, Разработка программных приложений | |
Perhaps, you might be interested in the following articles of similar topics:
- Схемотехнические САПР для персональных компьютеров
- Календарные расчеты на калькуляторе
- Программное обеспечение АРМ медицинского специалиста в области сосудистой патологии
- Прогнозирование эффективности систем хранения информации
- Учет когнитивных и поведенческих особенностей человека-эксперта при построении систем искусственного интеллекта

 По полученному описанию можно вывести статические свойства системы – максимальное используемое значение ресурса. MAGIC позволяет связать подобное описание с исходным кодом приложения, используя описания только небольшого числа стандартных функций, таких как функция выделения памяти. Когда подобное связывание вызывает затруднения, проверки на стадии выполнения с использованием функций PAPI и дополнительных библиотек дают возможность упростить задачу связывания, обеспечив проверку соответствия приложения заданной модели.
По полученному описанию можно вывести статические свойства системы – максимальное используемое значение ресурса. MAGIC позволяет связать подобное описание с исходным кодом приложения, используя описания только небольшого числа стандартных функций, таких как функция выделения памяти. Когда подобное связывание вызывает затруднения, проверки на стадии выполнения с использованием функций PAPI и дополнительных библиотек дают возможность упростить задачу связывания, обеспечив проверку соответствия приложения заданной модели.