Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм метода повышения адекватности модели для специализированных тренажеров
Аннотация:
Abstract:
| Автор: Григорьев И.А. () - | |
| Ключевые слова: рекурсивный алгоритм корректировки состояния системы, метод повышения адекватности модели общекорабельных систем, искажения численных решений, моделирование процессов массо- и теплопереноса |
|
| Keywords: , , , |
|
| Количество просмотров: 9916 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
Для разработки ряда специализированных тренажерных комплексов [1] была предложена методика моделирования общекорабельных систем (ОКС). При моделировании процессов массо- и теплопереноса по предлагаемой методике возникают нежелательные эффекты. Они проявляются в виде искажений решений численного моделирования, которые происходят при использовании в таких системах емкостей малого объема. Емкости, обладающие малым объемом, в большинстве моделируемых систем применяются в качестве трубопроводов, соединяющих емкости системы между собой. Искажения приводят к увеличению времени переходных процессов, то есть ухудшается адекватность модели ОКС.
Рис. 1 Для уменьшения искажений численных решений разработан метод повышения адекватности модели ОКС. Суть его заключается в корректировке численных решений (состояния емкостей/трубопроводов), получаемых численным методом на шаге интегрирования номер k, на основании введенных ограничений [2]. Рассмотрим алгоритмическую реализацию метода повышения адекватности модели ОКС.
Рис. 2 Введем обозначения: На рисунке 1 графически представлены ограничения массы жидкости и газа в емкости номер i на шаге интегрирования номер k при решении системы дифференциальных уравнений численным методом Эйлера [3]. На рисунке 2 представлены ограничения жидкости и газа в трубопроводе номер i. Область допустимых значений массы жидкости В качестве допустимых значений массы жидкости Корректировка состояния некоторой емкости/трубопровода номер i влечет за собой корректировки соседних с ней емкостей/трубопроводов с номерами
Рис. 3 Пусть
Рассмотрим рекурсивный алгоритм корректировки состояния системы на шаге интегрирования номер k. Блок-схема алгоритма корректировки изображена на рисунке 3. Для емкостей системы корректировка осуществляется только при нарушении граничных условий в отличие от трубопроводов, состояние которых корректируется на каждом шаге интегрирования в силу специфики предлагаемых для трубопроводов ограничений [2]. После завершения работы алгоритма корректировки состояния системы на k-м шаге осуществляется массоперенос вещества между емкостями и трубопроводами. Затем численным методом рассчитываются новые состояния емкостей/трубопроводов, которые корректируются предлагаемым рекурсивным алгоритмом, и т.д. В результате использования предлагаемого рекурсивного алгоритма корректировки состояния системы на каждом шаге интегрирования при численном моделировании ОКС в составе компьютерного тренажера повышена адекватность модели ОКС. Литература 1. Шукшунов В.Е., Циблиев В.В., Потоцкий С.И. и др. Тренажерные комплексы и тренажеры. Технологии разработки и опыт эксплуатации. – М.: Машиностроение, 2005. – 384 с. 2. Григорьев И.А. Метод повышения адекватности модели общекорабельных систем для тренажеров. // Программные продукты и системы. – 2008. – № 4. – С. 128–129. 3. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. – М.: Мир, 1980. – 279 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=1728&like=1&page=article |
Версия для печати Выпуск в формате PDF (8.40Мб) |
| Статья опубликована в выпуске журнала № 4 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



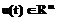

 (1)
(1)
 , (2)
, (2) , (3)
, (3)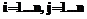 , (4)
, (4) . (5)
. (5)