Активная идентификация автоматизированных систем на основе вычислительного эксперимента
| Барщевский Е.Г. () - , Зубарев Ю.Я. () - , Солдатенко С.А. () - | |
| Ключевые слова: полиномиальные модели, вычислительный эксперимент, идентификация автоматизированных систем |
|
| Keywords: , computing experiment, |
|
|
|
|
Одной из важнейших проблем, возникающих при исследовании и оптимизации автоматизированных систем (АС), является их идентификация. Ее решение вызывает ряд трудностей, связанных со сложностью математического описания большинства АС и с большим числом противоречивых требований, предъявляемых к ним. Для повышения эффективности исследования и оптимизации перспективных АС необходимо создать комплекс согласованных и информационно совместимых математических моделей, в которых высокая точность и оперативность расчетов должны сочетаться с простотой реализации. При создании комплекса моделей АС целесообразно использовать концепцию активной идентификации сложных систем, основанную на планировании вычислительного эксперимента (ВЭ). Планирование ВЭ с помощью ПК на основе вычислительных моделей и обработка полученных результатов в соответствии с принятыми критериями оптимальности позволяют активно идентифицировать процессы в АС, то есть получить комплекс согласованных моделей АС, представляющих собой полиномиальные зависимости различных показателей качества процессов от параметров исследуемых АС и приложенных к ним внешних воздействий. Для повышения точности полиномиальных моделей (ПМ) необходимо выбирать планы ВЭ (ПВЭ) таким образом, чтобы минимизировать интегральную оценку ошибки аппроксимации, усредненную по заданным областям изменения параметров АС с учетом закона распределения этих параметров. Поэтому учет частоты проведения ВЭ при разработке осуществляется с помощью обобщенного критерия наименьших квадратов, предусматривающего минимизацию суммы взвешенных квадратов отклонений:
где Приравнивая к нулю произведение от суммы (1) и переходя к матричной форме записи, выражения для векторов коэффициентов ПМ можно представить в виде:
где Q – информационная матрица ПВЭ; Симметричные ПВЭ, как правило, состоят из отдельных симметричных конфигураций, которые представляют подмножества точек спектра плана, соответствующие характерным точкам правильных геометрических фигур, в частности, вершинам или центрам граней гиперкуба, звездным или центральным (нулевым) точкам. Задача синтеза непрерывных симметричных планов заключается в выборе типовых конфигураций, определении их размеров и частоты проведения экспериментов в точках спектров отдельных конфигураций, исходя из условий оптимальности, определяемых выбранным критерием. При этом предполагается, что точки спектра одной конфигурации имеют одинаковую частоту проведения экспериментов. Вместо необходимых и достаточных условий в работах по планированию эксперимента рекомендуется использовать достаточные условия оптимальности, что ужесточает требования к оптимальным планам. Поэтому определим в явном виде необходимые и достаточные условия оптимальности, которые представляют собой соотношения между моментами плана эксперимента и закона распределения параметров исследуемой системы. Для ПМ четвертого порядка указанные соотношения имеют следующий вид:
где По указанным соотношениям были составлены уравнения для моментов законов распределения параметров, решение которых позволило определить характеристики ПВЭ третьего и четвертого порядков, минимизирующих интегральную оценку аппроксимации. Синтез оптимальных планов четвертого порядка. Построим оптимальный план на четыре фактора для полинома четвертого порядка, который по точности максимально приближался бы к полиному пятого порядка. Используем для этого план, содержащий следующие конфигурации: два гиперкуба, ядро плана Бокса–Бенкина и три комплекта звездных точек. По условиям пропорциональности моментов плана и законов распределения параметров получаем следующую систему уравнений:
где Для удобства решения системы уравнений (3)–(8) разбиваем ее на 2 подсистемы уравнений: (3)–(5) и (6)–(8). В подсистеме уравнений (3)–(5) содержится только шесть неизвестных (
Из уравнений (3)–(5) численным методом определяются а1, а2, а3 с учетом положительности приведенных частот. В результате получено несколько решений. Из них берем вариант, основываясь на том, что размер одной из конфигураций должен быть близким к единице: а1=0,52; а2=0,75; а3=0,95. Приведенные моменты в уравнениях (3)–(5) представим следующим образом:
Тогда уравнения (6)–(8) принимают вид:
Решив систему уравнений (9), получим приведенные частоты:
Используя ранее полученные приведенные частоты проведения эксперимента В итоге получим характеристики оптимального ПВЭ четвертого порядка, которые приведены в таблице 1. Для сравнительной оценки точности полученных ПМ произведен расчет коэффициентов искажения кривой напряжения судовой электроэнергетической системы с трехфазными статическими выпрямителями. Сравнивались ПМ четвертого и третьего порядков, полученные на основе оптимального и традиционных планов. Таблица 1
Сравнение результатов расчетов коэффициентов искажения методом статистических испытаний позволило получить значения вероятностных характеристик ошибок, определяемых величинами коэффициентов испытаний моделей (табл. 2). Как видно из таблицы 2, использование оптимальных планов четвертого порядка значительно повышает точность полиномиальных моделей. Таблица 2
Полученные оптимальные планы эксперимента были использованы для определения ПМ показателя качества электромагнитных процессов при исследовании и оптимизации судовых электроэнергетических систем. Литература 1. Зубарев Ю.Я. и др. Планирование вычислительного эксперимента в электроэнергетике. – СПб. Энергоатомиздат, 2000. – 327 с. 2. Солдатенко С.А., Барщевский Е.Г. Сравнительная оценка планов вычислительного эксперимента третьего и четвертого порядка. // Сб. науч. тр.: Информационные технологии и системы: управление, экономика, транспорт, право. – Вып. 1. – СПб: Андреевский издат. дом. – 2008. – С. 21–24. | |||||||||||||||||||||||||||||||||||||||||||
http://swsys.ru/index.php?id=2004&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Методика оценки точности нейросетевых моделей
- Построение архитектуры САПР одношнековых экструдеров с применением элементов искусственного интеллекта
- Использование программного обеспечения для определения и прогнозирования показателей качества экструдированной продукции
- Прогнозирование времени обработки изображений детерминированными методами

 , (1)
, (1) и
и  – значения показателей в u-м спектре плана, полученные соответственно в результате ВЭ и на основе ПМ.
– значения показателей в u-м спектре плана, полученные соответственно в результате ВЭ и на основе ПМ. , (2)
, (2) – вектор-столбец значений показателей в точках спектра ПВЭ;
– вектор-столбец значений показателей в точках спектра ПВЭ;  – диагональная матрица частот проведения эксперимента.
– диагональная матрица частот проведения эксперимента.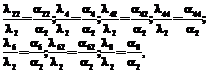
 ,
, ,
, ,
, ,
, ,
, – моменты плана;
– моменты плана;  – четные моменты законов распределения параметров. Эти соотношения – необходимые и достаточные условия минимизации интегральной оценки аппроксимации, положенные в основу синтеза непрерывных ПВЭ.
– четные моменты законов распределения параметров. Эти соотношения – необходимые и достаточные условия минимизации интегральной оценки аппроксимации, положенные в основу синтеза непрерывных ПВЭ.
 – размеры конфигураций;
– размеры конфигураций;  – приведенные частоты в отдельных конфигурациях проведения эксперимента
– приведенные частоты в отдельных конфигурациях проведения эксперимента  ,
,  , где h – коэффициент пропорциональности;
, где h – коэффициент пропорциональности;  – четные моменты второго, четвертого и шестого порядков законов распределения параметров.
– четные моменты второго, четвертого и шестого порядков законов распределения параметров. ), и ее аналитическое решение не представляется сложным. С этой целью выразим приведенные частоты проведения эксперимента в отдельных конфигурациях плана
), и ее аналитическое решение не представляется сложным. С этой целью выразим приведенные частоты проведения эксперимента в отдельных конфигурациях плана  через размеры конфигураций плана а1, а2, а3:
через размеры конфигураций плана а1, а2, а3: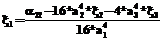 ,
, ,
, .
. ,
, ,
, .
. ,
, , (9)
, (9) .
. ,
, ,
, .
.