Оптимизация расписаний последовательно-параллельных обслуживающих систем
| Мезенцев Ю.А. (mesyan@yandex.ru) - Новосибирский государственный технический ун (профессор,), Новосибирск, Россия, доктор технических наук | |
| Ключевые слова: дерево решений, алгоритмы поиска кратчайшего расписания, смешанная сетевая модель, обслуживающие системы |
|
| Keywords: decision tree, , , |
|
|
|
|
Задачи календарного производственного планирования хорошо изучены и являются предметом исследования теории расписаний [1–3]. Однако до сих пор на практике точные методы их решения, обеспечивающие разработку наилучших по быстродействию или по другим критериям календарных планов, используются крайне редко. Одна из причин этого – чрезвычайная сложность логико-математического описания объектов управления. Другая серьезная проблема – отсутствие универсальных средств решения подобных задач в основном из-за их NP-полноты и значительных размерностей [4]. Особенно сложны задачи управления параллельно-последовательными обслуживающими системами. Тем не менее, общие подходы к их точному и приближенному решению существуют. Одному из таких подходов и посвящена данная статья.
Рис. 1 Рассмотрим обслуживающую систему, обладающую следующими характеристиками. Множество L={1,2,…,n} приборов разбито на P попарно непересекающихся непустых подмножеств L1,L2, …,Lp (групп, типов) приборов. Каждое подмножество Lp состоит из np идентичных (необязательно одинаковых) взаимозаменяемых приборов. На обслуживание поступает множество требований, обслуживаемых в течение планового периода в количестве m. Дисциплина обслуживания – без прерываний, то есть не позволяется прерывание обслуживания одного требования в пользу другого. Одним прибором одновременно может обслуживаться только одно требование. Технология обслуживания всех требований задается с помощью матрицы технологических маршрутов Необходимо определить такую очередность обслуживания требований приборами, при которой суммарное время обслуживания всех требований было бы минимальным. Возникают две взаимосвязанные задачи: 1) выбор очередности обслуживания каждого k-го (k= Данную ситуацию можно графически интерпретировать с помощью смешанной сетевой модели специального вида (рис. 1). При выполнении операций, отображаемых вершинами сети на рисунке 1, должен осуществляться выбор единственного варианта из альтернатив, определяемых множествами приборов Lp. Это отражено на рисунке с помощью сцепленных вершин. Каждой подобной сцепке соответствуют альтернативные варианты выполнения операции. Опишем модификацию вычислительной схемы метода ветвей и границ для решения представленной задачи. Пусть A – множество операций, включая фиктивные; U – множество логических условий предшествования-следования операций; V – множество логических условий неодновременности выполнения операций; G=(A,U,V) – некоторый оператор над множествами операций и логических условий, которым должен удовлетворять процесс обслуживания. В частности, G=(A,U,V) можно интерпретировать как смешанный граф с множествами вершин A, дуг U и ребер V. IG – множество индексов операций и логических условий, определяемых на G=(A,U,V). Для прозрачности нумерации обозначим тройкой (k,lp,q) операцию обслуживания требования k прибором lp в q-й по очереди раз. А для краткости будем полагать i=(k1,l1,q1), j=(k2,l2,q2) – номера операций из A. Через Uij обозначим дугу из U, соединяющую операции i и j (i предшествует j). Через Vij обозначим ребро из V между операциями i и j (Vij=Vji). Через Wij и Алгоритм ветвей и границ поиска кратчайшего расписания 1. Все ребра из V ранжируются по убыванию конфликтности, которая определяется количеством конкурирующих относительно одного и того же прибора требований в каждый интервал времени. Очевидно, что, чем меньше требований соотносится с некоторым Lp и (или) чем больше элементов содержится в Lp, то есть чем больше np, тем ниже конфликтность соответствующих ребер. Отбрасываются все ребра дизъюнктивной сети G=(A,U,V). Получаемый при этом граф G0= =(A,U,Æ) является временной моделью. Расписание, определяемое графом G0=(A,U, Æ), не является допустимым относительно исходных условий, но с его помощью можно получить первоначальную оценку нижней границы решения исходной задачи. 2. В соответствии с присвоенным рангом из множества V выбирается ребро Vij и в случае, когда соответствующее множество Lp состоит из одного элемента (np=1), заменяется парой дуг Wij и 3. Если же Vij опирается на прибор из множества Lp, которое содержит более одного элемента, то есть np>1 (сцепленные операции на рисунке 1), то из множества ребер Vij, ассоциируемых с приборами из Lp, формируются все возможные комбинации из двух ребер (рис. 2), каждое из которых заменяется дугой. Дуги при этом должны быть противоположной направленности. Каждая из дуг добавляется к текущей ослабленной (релаксированной) подзадаче, образуя новую подзадачу. Очевидно, что число порождаемых такой операцией альтернативных подзадач составляет величину 4. Методом критического пути (МКП) определяются нижние оценки решений каждой из вновь образованных подзадач. При np=1 процедура МКП определяется правилами [1]:
Для операций, выполняющихся на приборах из Lp (np>1), процедура МКП дополняется следующим правилом:
Подзадача, соответствующая наименьшей нижней оценке, проверяется на оптимальность. При оптимальном решении процесс завершается, иначе выполняется п. 5. 5. Подзадача с наименьшей нижней оценкой выбирается для дальнейшего ветвления, после чего осуществляется переход к п. 2. Числовой пример Пусть имеются приборы двух типов (один прибор 1-го типа и два 2-го),
Рис. 2 Соответствующая смешанная сеть G=(A,U,V) представлена на рисунке 2. Сдвоенными вершинами отображены операции, выполняемые параллельными приборами второго типа. Поскольку между двумя операциями над различными требованиями условия неодновременности обслуживания одним прибором отображаются с помощью одного ребра и одно требование может обслуживаться только одним из параллельных приборов, бинарное отношение порядка обслуживания двух требований приборами одной группы (одного типа) задается парой дуг противоположной направленности. Все ребра из V ранжируются по убыванию конфликтности, которая определяется количеством конкурирующих относительно одного и того же прибора требований в каждый интервал времени. В результате имеем:
Отбрасываются все ребра смешанной сети G=(A,U,V). Получаемый при этом релаксированный граф (РГ 1) G0=(A,U,Æ) является временной моделью. Его критическое время составляет 8 часов. Поэтому нижняя оценка длины расписания h0=8. На первом шаге в соответствии с принципом максимального приоритета выбираем переменную W111,211. При W111,211=1 образуем РГ 1.1, при W111,211=0 ( В дереве решений (рис. 3) допустимым временным моделям соответствуют концевые вершины. Рядом с каждой вершиной помещена временная оценка h соответствующего РГ. Символ Æ означает отсутствие решения (соответствующая временная модель содержит цикл).
Рис. 3 В результате получены два оптимальных решения (РГ 5.1, РГ 5.4), h*=10. В расписании РГ 5.4 (рис. 4) первый прибор второго типа не используется, что дает косвенный эффект (за счет экономии ресурсов). Поэтому в качестве оптимального решения принимается вектор:
Рис. 4 На рисунке 4 операции, принадлежащие критическим путям, соединены жирными стрелками. Приближенный алгоритм поиска кратчайшего расписания Приведенная модификация алгоритма ветвей и границ ограничена в применении, поскольку, как и любой другой комбинаторный алгоритм, не имеет полиномиальной от размерности решаемой задачи сходимости. Поэтому при решении практических задач теории расписаний значительных размерностей, относящихся к классу NP-полных, необходимо использовать приближенные модификации точных алгоритмов либо специальные приближенные методы поиска оптимумов. Рассмотрим такую модификацию представленного выше точного алгоритма синтеза оптимальных расписаний для быстрого приближенного решения поставленной задачи. 1. Множество ребер V смешанной сети G предварительно разбивается на упорядоченный ряд непересекающихся подмножеств Vq, Для этого определяются величина Q (количество подмножеств), число и состав элементов каждого подмножества. Количество элементов mq подмножеств Vq, Для решения вопроса о порядке и составе подмножеств будем использовать два способа: 1) включение ребер в очередное подмножество Vq в количестве mq в порядке следования операций в M, при этом целесообразно соблюдать принцип равномерности потоков операций относительно заявок; 2) включение ребер в очередное подмножество Vq в количестве mq в соответствии с их рангами (п. 1 алгоритма ветвей и границ). Образуются начальная временная модель G0=(A,U,Æ) и, как отмечалось ранее, недопустимое в общем случае расписание, порождаемое графом G0=(A,U,Æ), с оценкой нижней границы решения исходной задачи. 2. Из упорядоченного множества V=(V1,V2, …, VQ) выбирается очередное подмножество 3. В соответствии с рангом из множества Vq выбирается очередное ребро 4. Процедурой МКП определяются нижние оценки решений каждой из подзадач. Производится проверка на исчерпание подмножества Vq. Если Vq не исчерпано, то подзадача, соответствующая наименьшей нижней оценке, выбирается для ветвления, вычеркиваются дуги с номерами, следующими по очередности за 5. Производится проверка на окончание процесса, которое наступает при q=Q. В противном случае (q При q=Q подзадача, соответствующая наименьшей нижней текущей оценке, является временной моделью Для иллюстрации работы алгоритма вернемся к условиям числового примера: В результате применения алгоритма синтезируется нормальная бесконтурная сеть (рис. 5), порождающая субоптимальное по быстродействию расписание, которое на поверку совпадает с одним из оптимальных расписаний, полученных с помощью точного алгоритма. На рисунке 5 дуги Сравнивая дерево решений, полученное при использовании приближенного алгоритма (оконтуренная часть дерева на рис. 3), с деревом решений на основе точного алгоритма (полное дерево), можно сделать вывод о том, что первое является подмножеством второго. В общем случае это не всегда так. Можно предложить несколько оценок оптимального быстродействия обслуживающими системами в рамках приближенного алгоритма. В качестве нижней оценки критерия эффективности целесообразно использовать критическое время временной модели Верхней границей является критическое время временной модели Усредненной оценкой считаем критическое время модели Более точные оценки можно получить, исследуя различные разбиения V=(V1,V2,…,VQ), варьируя способы построения подмножеств Vq и величины mq, Подводя итог, отметим, что точный алгоритм синтеза оптимальных расписаний последовательно-параллельных обслуживающих систем на базе МВГ является частным случаем приближенного алгоритма (для Q=1).
Рис. 5 Используя приближенный алгоритм, необходимо находить разумный компромисс между точностью и трудоемкостью, которые легко регулируются параметрами алгоритма. Подобный подбор параметров предполагает активное вмешательство эксперта и подразумевает диалоговую процедуру. Кроме того, оба алгоритма применимы при относительно небольшом количестве параллельных приборов. В противном случае число комбинаций дуг между операциями, выполняемыми на соответствующем множестве приборов, становится необозримым, а затраты времени на поиск оптимального расписания неоправданными. Для расширения границ применения актуальна задача отбора эффективного ограниченного подмножества таких комбинаций. Литература 1. Танаев В.С., Сотсков Ю.Н., Струсевич В.А. Теория расписаний. Многостадийные системы. – М.: Наука, 1989. – 328 с. 2. Первозванский А.А. Математические модели в управлении производством. – М.: Наука, 1975. – 616 с. 3. Танаев В.С., Шкурба В.В. Введение в теорию расписаний. – М.: Наука, 1975. – 256 с. 4. Мезенцев Ю.А. Алгоритмы синтеза расписаний многостадийных обслуживающих систем в календарном планировании. / Омский научный вестник. – Омск: Изд-во ОГТУ, 2006. – № 3. – С. 97–102. |
http://swsys.ru/index.php?id=2007&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Методы оптимизации расписаний параллельных обслуживающих систем
- Прогнозирование аномалий в работе натяжных устройств агрегата полимерных покрытий металла в условиях малого количества отказов
- Разработка и внедрение модели прогнозирования цветового отклонения полимерного покрытия оцинкованной полосы
- Системный анализ факторов, определяющих способ прокладки городских инженерных коммуникаций
- Методы и модели выбора способа прокладки подземных инженерных коммуникаций в условиях городской застройки


 (маршруты произвольные) и соответствующего ей трехмерного объекта (трехвалентного тензора) длительностей обслуживания
(маршруты произвольные) и соответствующего ей трехмерного объекта (трехвалентного тензора) длительностей обслуживания  (также произвольных); k-й технологический маршрут содержит dk операций, dk
(также произвольных); k-й технологический маршрут содержит dk операций, dk
 , где
, где  , k=
, k= . Сечения по индексу k (k=
. Сечения по индексу k (k= обслуживания требования k приборами из L. В частности, если все множества L1,L2, …,Lp содержат по одному элементу, то T=
обслуживания требования k приборами из L. В частности, если все множества L1,L2, …,Lp содержат по одному элементу, то T= – матрица, равная по размерности M.
– матрица, равная по размерности M. ), определяемой маршрутом из M; 2) назначение (закрепление) каждого требования за конкретным прибором из выбранного Lp.
), определяемой маршрутом из M; 2) назначение (закрепление) каждого требования за конкретным прибором из выбранного Lp. обозначим пару дуг, заменяющих ребро Vij, где
обозначим пару дуг, заменяющих ребро Vij, где 
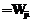 . Заметим, что для обозначения ориентации дуг достаточно булевых переменных: Wij=1 и
. Заметим, что для обозначения ориентации дуг достаточно булевых переменных: Wij=1 и  . Обозначим также через W множество дуг, заменяющих все ребра из V, которое порождает бесконтурную сеть Gt=(A,UW,Æ), где
. Обозначим также через W множество дуг, заменяющих все ребра из V, которое порождает бесконтурную сеть Gt=(A,UW,Æ), где  , называемую временной моделью. Тогда формально задача состоит в нахождении такого W*, которое порождает временную модель, определяющую расписание минимальной длины.
, называемую временной моделью. Тогда формально задача состоит в нахождении такого W*, которое порождает временную модель, определяющую расписание минимальной длины.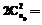

 .
.

 ,
, 

 .
.

 ;
; ,
,  .
.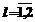 , на которых обрабатываются два требования,
, на которых обрабатываются два требования,  . При этом
. При этом  ;
;  .
.
 .
. ) – РГ 1.2. Аналогично порождаются прочие РГ в соответствии с вычислительной схемой метода ветвей и границ.
) – РГ 1.2. Аналогично порождаются прочие РГ в соответствии с вычислительной схемой метода ветвей и границ.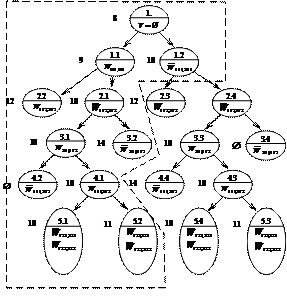
 .
.
 , то есть V=
, то есть V=

 .
. , может быть как различным, так и одинаковым. В последнем случае целесообразно использовать, например, mq= =
, может быть как различным, так и одинаковым. В последнем случае целесообразно использовать, например, mq= = ,
,  , и
, и 
 , где
, где  – целая часть отношения
– целая часть отношения  .
. (на первом шаге q=1 и Vq=V1).
(на первом шаге q=1 и Vq=V1). , заменяется парой дуг
, заменяется парой дуг  и
и  , каждая из которых добавляется к текущей ослабленной подзадаче, в результате чего образуется пара новых подзадач с номерами (
, каждая из которых добавляется к текущей ослабленной подзадаче, в результате чего образуется пара новых подзадач с номерами ( ) и (
) и ( ).
). , где
, где  =
= , порождающей наилучшее для данного алгоритма расписание.
, порождающей наилучшее для данного алгоритма расписание.
 , разобьем его на три подмножества: V={V1,V2,V3}:
, разобьем его на три подмножества: V={V1,V2,V3}:  ,
,  ,
,  .
. , для q=1 изображены сплошными линиями, для q=2 – пунктирными, для q=3 – штрихпунктирными линиями.
, для q=1 изображены сплошными линиями, для q=2 – пунктирными, для q=3 – штрихпунктирными линиями. , q=1.
, q=1. , q=Q.
, q=Q. , где
, где  .
. .
.