Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование состояния и поведения судна на базе фильтра Калмана
Аннотация:
Abstract:
| Авторы: Трояновский Я. () - , Арефьев И.Б. (i.arefyev@am.szczecin.pl) - Морская академия , Щецин, Польша, доктор технических наук | |
| Ключевые слова: дискретный наблюдатель, белый шум, алгоритм фильтрации, фильтр калмана, модель поведения судовых динамических систем |
|
| Keywords: , , , Kalman filter, |
|
| Количество просмотров: 13606 |
Версия для печати Выпуск в формате PDF (3.60Мб) |
Моделирование судовых систем управления в реальном масштабе времени условно подразделено на шесть ступеней: сбор данных, сетевые топологические вычисления, анализ наблюдаемости, оценка состояния, обработка «плохих» данных, идентификация параметров сигналов и управляемых объектов по экспериментальным данным. Одним из реальных решений указанной проблемы является применение фильтра Калмана и его развитие в формировании дискретного наблюдателя, структура которого предполагает снижение объема вычислений для реального построения модели поведения судовых динамических систем. Для класса моделей в форме разностных уравнений
(где r – целые числа на множестве [1,k]) разработан рекурсивный метод оценивания и рассмотрены его приложения для идентификации параметров судовых динамических систем, где Фильтр Калмана конструируется в виде динамической системы с переменным матричным коэффициентом усиления, величина которого зависит от точности текущих значений и уровня шумов измерений. Дискретный вариант фильтра основан на рекуррентных соотношениях, выполняемых согласно алгоритму, что создает удобства для его реализации на ЭВМ. Поскольку параметры Калмана изменяются во времени, критерий качества (минимум среднеквадратической ошибки оценивания) минимизируется как в установившихся, так и в переходных режимах. Оптимальная оценка относительно наблюдений является линейной [1]. Вследствие линейности фильтра корреляционная матрица ошибок фильтрации не зависит от наблюдений. Она может быть вычислена заранее как матричный коэффициент усиления фильтра. Алгоритм фильтрации пригоден к использованию как в одноканальных, так и в многоканальных системах [2]. В случае концептуально строгой постановки задачи фильтрации должны составляться стохастические дифференциалы Ито, поскольку белый шум с непрерывным временем представляется чистой идеализацией, и как в математическом, так и физическом смыслах можно говорить лишь о существовании его интеграла, то есть винеровского процесса [3]. Для синтеза фильтра Калмана–Бьюси с использованием моделей, построенных на обыкновенных дифференциальных уравнениях и сигналах в форме белых шумов, введены допущения, позволяющие упростить задачу. Предполагается, что управляемый объект описывается с помощью стохастических уравнений динамики
y(t)=C·х(t)+v(t) (3) c вектором состояния
Предположение о том, что w(t) и v(t) являются белым шумом, может быть в некоторых случаях ослаблено. Воздействия волн и ветра на корпус судна имеют ограниченный спектр, следовательно, w(t) не является белым шумом. Поэтому необходимо идентифицировать параметры динамической системы, преобразующей входной сигнал в виде белого шума n(t) в сигнал w(t), адекватно отражающий процесс воздействия помехи на объект. Для восстановления вектора состояния по вектору выхода в стохастической системе, функционирующей во внешней среде, применен динамический наблюдатель:
или Изменяющаяся во времени функция
является оценкой выхода y(t), представляющей собой условное среднее, полученное по предшествующим измерениям. Матрица коэффициентов оценивателя L обеспечивает оптимальную оценку вектора состояния при наличии шумов w(t) и v(t). Ошибка оценивателя определяется как разность сигналов
Дифференциальное уравнение для расчета ковариационной матрицы имеет вид
Решение (9) находится при условии Р(0)=Р0, то есть ковариационной матрице начального состояния, характеризующей неопределенность в оценке Учет ограничений на вектор управления и состояния в судовых дискретных апериодических системах методологически может быть выполнен с помощью вычислительных процедур, основанных на псевдоинверсии Мура–Пенроуза. Дискретная модель судна как объекта управления представлена в виде хd(k+1)=Adхd(k)+Вdu(k), k≥0, (10) где хd – (n´1)-мерный вектор состояния; u(k) – последовательность управления для k=0,1,…,N-1 (N≥n); Ad, Вd – матрицы соответствующих размерностей. Согласно принципу Заде, дискретные управления u(k) обеспечивают переход системы из начального состояния хd(0) в конечное хd(N) за конечное число шагов, не меньшее n. Вектор выхода получен с помощью уравнения y(k)=Cd хd(k), (11) где y(k) – (m´1)-вектор, причем m Матрица Сd имеет полный ранг m и представляется в виде двух блоков: несингулярной (m´m) – матрицы С1 и (m´(n-m)) – матрицы С2: Cd=[C1C2]. (12) Условие (12) позволяет преобразовать исходную систему (10)–(11) к канонической форме: x(k+1)=Ax(k)+Bu(k), (13) y(k)=Cx(k), (14) где
Преобразование переменных состояния выполняется с помощью матрицы Tpr, которую можно получить, используя соответственно матрицы достижимости для исходной системы
и системы в канонической форме
Преобразующая матрица Tpr находится по формуле Тpr=Рd·P-1. (15) Для системы (13)–(14) можно синтезировать дискретный наблюдатель, структура которого дает возможность значительно уменьшить объем вычислений, необходимых для решения матричного уравнения TA–FT=HC, являющегося условием Луенбергера для построения наблюдателя F. Таким образом, синтезируется наблюдатель, структура которого дает возможность существенно сократить процедуру подготовки и принятия решения по управлению судном. Литература 1. Арефьев И.Б., Мартыщенко Л.А. Теория управления. – СПб: СЗТУ, 2000. – 173 с. 2. Трояновский Я. Концепция построения автоматизированных систем управления движением судов в районе водных путей и судоходства Нижней Одры. // Междунар. межвуз. сб. науч. тр. – СПб: Судостроение, 2006. – № 7. – С. 157–160. 3. Арефьев И.Б., Трояновский Я. Автоматизация судопропуска на внутренних водных путях. – СПб: Система, 2007. – 251 с.
|
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2014&page=article |
Версия для печати Выпуск в формате PDF (3.60Мб) |
| Статья опубликована в выпуске журнала № 1 за 2009 год. [ на стр. 39 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Нейро-нечеткий метод снижения чувствительности решения обратных задач к вариациям данных
- Прогноз состояния объекта на основе применения фильтра Калмана и глубоких нейронных сетей
- Интервально-дифференциальные уравнения в структуре нечеткого фильтра Калмана при управлении сложными технологическими объектами
- Фильтр Калмана как метод вторичной обработки информации с системы ГЛОНАСС
- Нечеткий фильтр калмана в структуре алгоритма решения обратных задач для экономических объектов
Назад, к списку статей



 (1)
(1) и
и  – оцениваемые коэффициенты.
– оцениваемые коэффициенты. =A+B·u(t)+G·w(t), (2)
=A+B·u(t)+G·w(t), (2)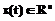 , входом
, входом 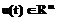 и измеряемым выходом
и измеряемым выходом  . Сигнал w(t) – неизвестный случайный сигнал, воздействующий на объект. В приложении к модели судна этот сигнал может характеризовать воздействие на управляемый объект ветра, волнения водной поверхности, а также не учитываемые в процессе моделирования высокочастотные составляющие динамических уравнений. Сигнал v(t) представляет собой неизвестный случайный процесс, вызванный сенсорными свойствами измерителей текущих переменных состояния и выхода. Поскольку (2)–(3) представляют собой динамическую модель, на которую воздействует шум, состояние х(t), а также выход y(t) являются, в свою очередь, также случайными процессами. Начальное условие x(0), шум процесса w(t), шум измерения v(t) точно неизвестны. Поэтому на практике следует руководствоваться некоторыми концептуальными положениями об их общих характеристиках. Используя концептуальный подход, далее следует формализовать эти положения и сформулировать в их терминах требования к рассчитываемой системе управления. Резонно предположить, что x(0), w(t) и v(t) взаимно ортогональны. На основании опыта можно получить среднее значение
. Сигнал w(t) – неизвестный случайный сигнал, воздействующий на объект. В приложении к модели судна этот сигнал может характеризовать воздействие на управляемый объект ветра, волнения водной поверхности, а также не учитываемые в процессе моделирования высокочастотные составляющие динамических уравнений. Сигнал v(t) представляет собой неизвестный случайный процесс, вызванный сенсорными свойствами измерителей текущих переменных состояния и выхода. Поскольку (2)–(3) представляют собой динамическую модель, на которую воздействует шум, состояние х(t), а также выход y(t) являются, в свою очередь, также случайными процессами. Начальное условие x(0), шум процесса w(t), шум измерения v(t) точно неизвестны. Поэтому на практике следует руководствоваться некоторыми концептуальными положениями об их общих характеристиках. Используя концептуальный подход, далее следует формализовать эти положения и сформулировать в их терминах требования к рассчитываемой системе управления. Резонно предположить, что x(0), w(t) и v(t) взаимно ортогональны. На основании опыта можно получить среднее значение  и ковариацию Р0, то есть
и ковариацию Р0, то есть . (4)
. (4) (5)
(5) . (6)
. (6) , равная
, равная , (7)
, (7) . (8)
. (8) (9)
(9) . Ковариация Р – мера неопределенности оценивания.
. Ковариация Р – мера неопределенности оценивания. ,
,  ,
, .
.
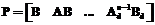 .
.