Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Система управления розничными продажами одного вида товара
Аннотация:
Abstract:
| Авторы: Дрозин Д.А. () - , Ширяев В.И. () - | |
| Ключевые слова: приверженность потребителей, конкурентоспособность, управление продажами, модель рынка одного вида товара |
|
| Keywords: , , , |
|
| Количество просмотров: 8729 |
Версия для печати Выпуск в формате PDF (3.60Мб) |
Сегодня активно развиваются информационные системы, позволяющие систематизировать данные о состоянии магазина [1], в частности, системы, способные обрабатывать соответствующие данные и формировать рекомендации по управлению магазином, но только на основе его внутренней информации. В данной работе описывается построение модели рынка одного вида товара, на основе которой можно вырабатывать рекомендации менеджерам магазинов по управлению продажами, используя не только внутреннюю информацию магазина, но и информацию о конкурентах, что расширяет область рекомендаций. С точки зрения понимания и описания конкурентоспособности фирм неоклассическая экономическая теория [2] уступает эволюционной теории: в построенных моделях рынка конкурентоспособность фирм определяется конкурентоспособностью производимых ими товаров (ценой и другими характеристиками). Поскольку магазин имеет свою специфику (его доход зависит от ценовой, ассортиментной политики, выкладки товара и т.п.), учитывая только конкурентоспособность товара, достоверно описать розничный рынок вряд ли удастся. В связи с этим при моделировании розничного рынка будем исходить из конкурентоспособности самого магазина [3,4]. В данной работе руководствуемся тем, что выручка магазина определяется главным образом приверженностью потребителей к этому магазину. А поскольку такая зависимость плохо формализуется, построим ее на основе логических рассуждений. Аппроксимировать зависимости в случае необходимости будем наиболее простыми функциями, чаще всего линейными. Модель рынка Под рынком будем понимать совокупность n магазинов и совокупность потребителей, вступающих в контакт с целью купли-продажи товара. Совокупность потребителей рассмотрим как сумму денежных средств Np (потенциал рынка), которую потребители рынка готовы потратить на данный вид товара (например, мыло весом 90 граммов) за некоторый промежуток времени Tp. Полагаем, что доля i-го магазина в Np зависит от того, насколько привлекательнее потребителям приобретать товар в этом магазине, нежели в других. Рассмотрим зависимости привлекательности i-го магазина от цены Pi и ассортимента Asi товара, так как цена и ассортимент имеют наиболее важное значение для потребителей, где Pi – средняя цена подвидов товара; Asi – количество подвидов товара. Например, 90-граммовое мыло в i-м магазине, допустим, имеет три подвида: с глицерином – 15 руб., с земляникой – 18,5 руб. и с вишней – 20 руб., тогда цена товара будет
Выражение запишем в виде
где Деление рынка имеет большое значение и рассматривается с разных точек зрения [2]. Будем полагать, что доля выручки i-го магазина в Np равна отношению привлекательности i-го магазина к сумме привлекательностей всех магазинов, то есть
Очевидно, что при резком изменении привлекательности Fi i-го магазина выручка изменится не сразу. Это связанно с тем, что должно пройти время, прежде чем потребители узнают об этом из рекламы и слухов. Будем полагать, что модель распространения информации за счет слухов и рекламы магазина аналогична описанной в [5]. В нашем случае люди соотносятся с их денежными средствами, значит, и в модели рассмотрим не количество людей, а их денежные средства. При этом модель определяет влияние рекламы и слухов среди потенциальных потребителей i-го магазина: где
где k – некий коэффициент. Принятие управленческих решений Для принятия управленческого решения в i-м магазине часто используется в качестве критерия прибыль Ii за некоторый промежуток времени Ti, зависимость которой имеет вид
где Pper i – закупочная цена; Ni – выручка в текущий момент t; Ti – конечный момент i-го магазина; T0 – начальный момент. На принятие управленческого решения также действует ограничение по ресурсам i-го магазина, которое имеет вид
где ZP i – затраты на изменение цены; ZAs i – затраты на изменение ассортимента (при увеличении ассортимента требуется закупать новый товар); hi – затраты на рекламу. Затраты на понижение цены на товар
где Pold i и Pnew i – цена товара в i-м магазине до изменения и после соответственно;
где N0 – выручка i-го магазина в момент T0. Таким образом, предложенная модель рынка (1)–(4) привела к задаче оптимального управления. Управляющие параметры Pi, Asi, hi, Ограничения на денежные ресурсы i-го магазина Ri заданы зависимостью (6). Целевым функционалом, максимум которого требуется найти, является прибыль
Данную задачу можно классифицировать как задачу Лагранжа. Уравнение движения задано уравнением (3) с учетом зависимостей (1), (2), (4). Решив задачу оптимального управления (1)–(4), (6)–(9), найдем оптимальные значения управляющих параметров Pi, Asi, hi только для i-го магазина. Считаем, что остальные магазины не принимают никаких новых управленческих решений. Решение задачи оптимального управления сводится к нахождению экстремума (максимума Ii) в четырехмерном евклидовом пространстве, где три управляющих параметра: Pi, Asi, hi, Приведем пример поведения рынка с двумя магазинами, n=2. На рисунке отображена динамика выручки (верхние кривые) и прибыли двух магазинов (нижние кривые) в зависимости от изменения управляющих параметров: цены Pi, ассортимента Asi и рекламы hi i-го магазина. Сплошной линией обозначена динамика первого магазина, пунктирной – динамика второго. Предлагается модель рынка одного вида товара для управления продажами. Модель позволяет по характеристикам рынка и магазинов, а также по потенциалу рынка прогнозировать поведение как отдельных магазинов, так и всего рынка в целом, что дает возможность формировать рекомендации по управлению ценой, ассортиментом и рекламой отдельных магазинов. Модель построена так, что позволяет дополнительно включать в нее другие факторы: качество обслуживания, расстояние до магазина и многое другое, для этого необходимо включить эти факторы в зависимость (1) по аналогии с факторами цены и ассортимента. На основе предложенной модели возможна разработка программного обеспечения поддержки принятия управленческих решений в магазине. Литература 1. Винокуров Л.Л. Технологии управления современным предприятием. // Информационные технологии. – 2005. – № 1 (Прилож.). – 32 с. 2. Коуз Р. Фирма, рынок и право. – М.: Дело ЛТД, 1993. – 192 с. 3. Ширяев В.И., Баев И.А., Ширяев Е.В. Управление фирмой: Моделирование, анализ, управление. – М.: Изд.-во ЛКИ, 2007. – 272 с. 4. Ширяев В.И., Баев И.А., Ширяев Е.В. Экономико-математическое моделирование управления фирмой. – М.: КомКнига, 2006. – 224 с. 5. Bass F. A new product growth model for consumer durables // Management Science. 1969. V. 15. pp. 215–227. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2022&page=article |
Версия для печати Выпуск в формате PDF (3.60Мб) |
| Статья опубликована в выпуске журнала № 1 за 2009 год. [ на стр. 56 ] |
Назад, к списку статей



 руб., а ассортимент
руб., а ассортимент  . Зависимость привлекательности
. Зависимость привлекательности  i-го магазина от цены Pi и ассортимента Asi товара имеет вид:
i-го магазина от цены Pi и ассортимента Asi товара имеет вид: ,
, , где Pcp – средняя цена товара по магазинам,
, где Pcp – средняя цена товара по магазинам,  ; Amax – количество возможных подвидов товара на данном рынке;
; Amax – количество возможных подвидов товара на данном рынке; 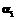 – константа, отражающая неучтенные привлекательности (качество обслуживания, выкладка товара в i-м магазине и т.д.); g – добавочная доля средней цены Pcp товара на рынке, при которой
– константа, отражающая неучтенные привлекательности (качество обслуживания, выкладка товара в i-м магазине и т.д.); g – добавочная доля средней цены Pcp товара на рынке, при которой 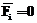 , k2 – некий коэффициент.
, k2 – некий коэффициент.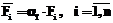 , (1)
, (1) .
. . (2)
. (2) , (3)
, (3) – выручка i-го магазина в установившемся режиме (2); Ni – выручка i-го магазина в момент t (например день); b – коэффициент, отображающий влияние слухов, распространяемых между людьми, на выручку магазина; ai – доля денег, привлеченных рекламой i-го магазина, потому
– выручка i-го магазина в установившемся режиме (2); Ni – выручка i-го магазина в момент t (например день); b – коэффициент, отображающий влияние слухов, распространяемых между людьми, на выручку магазина; ai – доля денег, привлеченных рекламой i-го магазина, потому  . Установим зависимость эффективности рекламы ai от денежных вложений i-го магазина. Пусть hi – доля вложенных в рекламу i-м магазином денежных средств, необходимых для привлечения всех потребителей. Будем считать, что, с одной стороны, скорость изменения ai в зависимости от hi прямо пропорциональна hi, с другой стороны, при достижении значения ai единицы (реклама охватывает всех потребителей рынка, то есть нет больше смысла вкладывать в нее деньги) и
. Установим зависимость эффективности рекламы ai от денежных вложений i-го магазина. Пусть hi – доля вложенных в рекламу i-м магазином денежных средств, необходимых для привлечения всех потребителей. Будем считать, что, с одной стороны, скорость изменения ai в зависимости от hi прямо пропорциональна hi, с другой стороны, при достижении значения ai единицы (реклама охватывает всех потребителей рынка, то есть нет больше смысла вкладывать в нее деньги) и  пропорциональна 1–ai. Итак, окончательно полагаем
пропорциональна 1–ai. Итак, окончательно полагаем  =k×hi×(1–ai). Решая уравнение и подставляя нулевую точку, получим
=k×hi×(1–ai). Решая уравнение и подставляя нулевую точку, получим
 , (5)
, (5) , (6)
, (6) , (7)
, (7) , (8)
, (8) . Вложение денег в рекламу может быть любым, поэтому
. Вложение денег в рекламу может быть любым, поэтому  . Цена товара Pi строго больше закупочной:
. Цена товара Pi строго больше закупочной: 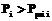 – это нижняя граница цены, что касается верхней ее границы, то считаем, что она не больше средней цены на рынке, умноженной на некоторый коэффициент
– это нижняя граница цены, что касается верхней ее границы, то считаем, что она не больше средней цены на рынке, умноженной на некоторый коэффициент  :
:  , и поэтому
, и поэтому  .
.
 . (9)
. (9)