Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм расчета предельных возможностей стационарных тепломеханических систем
Аннотация:
Abstract:
| Автор: Ахременков А.А. () - | |
| Ключевые слова: тепломеханические системы, тепломеханический преобразователь, оптимизационная термодинамика |
|
| Keywords: , , |
|
| Количество просмотров: 8546 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
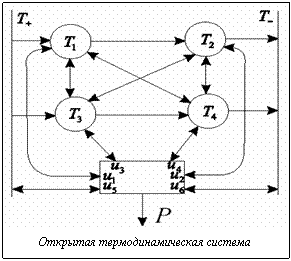
Термодинамика при конечном времени получила первый толчок для своего развития в задаче о цикле тепловой машины с максимальной мощностью [1, 2]. При этом в большинстве работ рассматривалась система, состоящая из тепловой машины и нескольких резервуаров с заданными и постоянными температурами [3]. Между тем эта задача особенно актуальна для систем, состоящих из термических резервуаров и подсистем конечной емкости с различающимися температурами, находящихся в контакте с резервуарами и друг с другом (см. рис.). В такой системе с отличающимися друг от друга температурами резервуаров при заданных законах и коэффициентах теплопереноса устанавливается стационарный режим, характеризующийся распределением температур между подсистемами и дискретным температурным полем. При этом каждая подсистема (резервуар, подсистемы конечной емкости и тепловая машина) считается внутренне равновесной, так что необратимые эффекты возникают на границах подсистем. Только при этих допущениях для каждой подсистемы справедливо термодинамическое описание. Такие системы в литературе называют endoreversible-системами. Естественно возникает вопрос, какую максимальную мощность можно извлечь в стационарной термодинамической системе с использованием тепловой машины, имеющей заданные коэффициенты теплообмена при контакте с каждым элементом системы. Назовем это задачей о максимальной мощности. В такой постановке она обобщает задачу И.И. Новикова [1]. Математическое описание Рассмотрим термодинамическую систему (структура ее представлена на рисунке), состоящую из (n-m) резервуаров с постоянными температурами, m подсистем конечной емкости, температуры которых определяются запасом их внутренней энергии. Каждая подсистема может контактировать с любой подсистемой и резервуаром, к ней могут подводиться конвективные потоки тепла извне qiK. Потоки обмена теплом подсистем друг с другом обозначим как qij(Ti, Tj). Эти потоки связаны с различием температур подсистем. Будем считать, что поток положителен qij(Ti, Tj)>0, если тепло поступает к i-й подсистеме, то есть Ti qij(Ti, Tj) – непрерывная и непрерывно дифференцируемая по совокупности аргументов; qij(Ti, Tj)=– qji(Tj, Ti);
Последнее свойство характерно для систем теплообмена.
где qi – суммарный поток тепла, подводимый к подсистеме; Ci – ее теплоемкость. Рассмотрим стационарное состояние тепломеханической системы, содержащей тепловую машину, которая может контактировать с подсистемами, получая или отдавая им потоки тепла, потребляя или вырабатывая мощность. Требуется найти такие температуры контакта ui рабочего тела тепловой машины с каждой из подсистем, при которых получаемая в единицу времени работа (мощность P) максимальна. Если максимальная мощность отрицательна, то она соответствует минимуму затрат подводимой извне энергии (в этом случае тепломеханическим преобразователем является тепловой насос). Постановка задачи и условия оптимальности Обозначим через ui температуру рабочего тела при контакте с i-й подсистемой; qij(Ti, Tj) – поток тепла между i-й подсистемой и преобразователем; P – мощность преобразователя. Поток, поступающий в каждую из подсистем, будем считать положительным. Формализуем задачу о максимальной мощности:
при условиях
Критерий (2) следует из энергетического баланса рабочего тела преобразователя. Условие (3) вытекает из энтропийного баланса рабочего тела, а (4) – энергетический баланс для i-й подсистемы конечной емкости. Предположим, что потоки qi, qij линейно зависят от разности температур
где Очевидно, что при числе резервуаров, большем или равном двум, и различающихся температурах резервуаров максимальная мощность положительна. Разобьем задачу на три подзадачи. 1. Максимизировать извлекаемую мощность
при условии
2. Максимизировать извлекаемую мощность
при условии
и балансовых соотношениях (4). 3. Найти максимальную суммарную мощность при условии баланса по энтропии для рабочего тела преобразователя, производство энтропии в котором равно нулю:
Первая из этих задач рассмотрена в работе [4] для случая
Максимальная мощность, извлекаемая при контакте с резервуарами:
с ростом Во второй задаче требуется найти не только температуры контактов ui, но и температуры подсистем Ti для i=1, …, m. Выразим ui через qi и Ti при условии, что потоки тепла заданы в ньютоновской форме (5):
и перепишем балансовые соотношения (4) как систему линейных уравнений относительно температур подсистем Ti, i=1, …, m:
Или в матричной форме: где
Обозначим элементы матрицы
При этом Перейдем от задачи (8), (9), (4) относительно ui, Ti к оптимизационной задаче относительно потоков тепла qi:
Выпишем функцию Лагранжа для задачи (17):
Условие ее стационарности по qj примет форму
Решив систему из m+1 уравнений (19), (9) относительно qi, находим оптимальные значения В третьей задаче требуется найти максимальную суммарную мощность, извлекаемую из резервуаров и подсистем. Выпишем функцию Лагранжа задачи (10):
Из условия стационарности функции Лагранжа по
Так как производные
Приведем алгоритм расчета максимальной мощности, извлекаемой тепломеханическим преобразователем. Поскольку решение задачи разделено на три этапа, рассмотрим поэтапный алгоритм. 1. Заданные переменные: температуры резервуаров Ti, i=m+1, n [K]; матрица коэффициентов теплопереноса 2. Выпишем алгоритм нахождения максимальной извлекаемой мощности при контакте с резервуаром при заданном значении а) найдем значение приведенной температуры контакта б) найдем значения максимальной извлекаемой мощности как функцию потока энтропии 3. Выпишем алгоритм нахождения максимальной извлекаемой мощности при контакте с подсистемами. Поскольку для решения этой задачи необходимо решить систему из m+1 уравнений (19), (9) относительно qi и а) обратим матрицу б) составим матрицу Якоби
в) в качестве начального приближения возьмем qi0=0, г) найдем следующие приближения:
д) вычислим значение функции F в точке qk+1 е) найдя оптимальные значения 4. Вычислим значения 5. Решим вторую задачу для 6. Если 7. Вычислим значение извлекаемой мощности для полученных оптимальных Пример. Рассмотрим систему, состоящую из двух резервуаров, четырех подсистем и преобразователя. Структура системы показана на рисунке. Матрица коэффициентов теплопереноса имеет вид
Значения aij при i, j=1, ..., 4 соответствуют коэффициентам взаимодействия подсистем между собой, значения при i>4 или j>4 – коэффициентам взаимодействия подсистем c резервуарами. Температуры резервуаров: T+=700 K, T-=300 K. Коэффициенты теплопереноса при взаимодействии преобразователя с подсистемами и резервуарами:
Значения ai при i=1, ..., 4 соответствуют коэффициентам взаимодействия с подсистемами, а при i>4 – коэффициентам взаимодействия c резервуарами. Коэффициенты имеют размерность Вт/К. Сначала были найдены значения После этого находились оптимальные В результате были получены следующие значения оптимальных температур: T1=564,8 K; T2=540,2 K; T3=563,7 K; T4=527 K. Оптимальные температуры контакта преобразователя с подсистемами: u1=557,8 K; u2=543,6 K; u3=557,7 K; u4=536,3 K; u5=620,2 K; u6=406 K. Значение предельной извлекаемой мощности P*=3,22 кВт. В работе получены оценки максимальной извлекаемой мощности для произвольной стационарной термодинамической системы и соответствующие ей распределения потоков тепла и температур контакта рабочего тела с подсистемами. Предложен алгоритм расчета максимальной извлекаемой мощности и оптимальных характеристик тепловой машины. Литература 1. Novikov I.I. The efficiency of atomic power stations // J. Nuclear Energy II. 1958. № 7, pp. 25–128. 2. Curzon F.L., Ahlburn B. Efficiency of a Carnot engine at maximum power output. Amer.J. Physics. 1975. № 43, pp. 22–24. 3. Amelkin S.A., Andresen B., Burzler J.M., Hoffmann K.H., Tsirlin A.M. Maximum power processes for multi-source endoreversible heat engines J. Phys. D: Appl. Phys. 2004. № 37, pp. 1400–1404. 4. Tsirlin A.M., Kazakov V., Ahremenkov A.A., , Alimo- va N.A. Thermodynamic constraints on temperature distribution in a stationary system with heat engine or refrigerator // J. Phys. D: Appl. Phys. 2006. № 39, pp. 4269–4277. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2256&page=article |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Назад, к списку статей



 ;
; ;
;  .
. Температура подсистем зависит от запаса внутренней энергии и изменяется в результате подвода (отвода) тепла к ней:
Температура подсистем зависит от запаса внутренней энергии и изменяется в результате подвода (отвода) тепла к ней: , (1)
, (1) (2)
(2) ; (3)
; (3) (4)
(4) (5)
(5) – коэффициенты теплопереноса. Такой закон теплообмена называют ньютоновским.
– коэффициенты теплопереноса. Такой закон теплообмена называют ньютоновским. при контакте преобразователя с резервуарами для заданного значения
при контакте преобразователя с резервуарами для заданного значения  – потока энтропии от резервуаров к рабочему телу
– потока энтропии от резервуаров к рабочему телу (6)
(6) . (7)
. (7) при контакте преобразователя с подсистемами конечной емкости для заданного значения
при контакте преобразователя с подсистемами конечной емкости для заданного значения  – потока энтропии от подсистем к рабочему телу
– потока энтропии от подсистем к рабочему телу (8)
(8) (9)
(9) . (10)
. (10) , где показано, что для ньютоновского теплообмена значение приведенной температуры контакта
, где показано, что для ньютоновского теплообмена значение приведенной температуры контакта  определяется как
определяется как (11)
(11) ; (12)
; (12) , (13)
, (13) . (14)
. (14) ,
,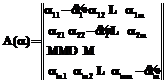 , (15)
, (15) ,
,  .
. через
через  , а элементы обратной ей матрицы A-1 через
, а элементы обратной ей матрицы A-1 через  и выразим температуры подсистем через потоки qi и заданные температуры резервуаров:
и выразим температуры подсистем через потоки qi и заданные температуры резервуаров: (16)
(16) .
. при условии
при условии . (17)
. (17) . (18)
. (18)
 . (19)
. (19) и
и  , а затем значения
, а затем значения  ,
,  и
и  . При таком решении удобнее задавать не
. При таком решении удобнее задавать не  , затем по формуле (9) рассчитывать соответствующее решению значение потока энтропии
, затем по формуле (9) рассчитывать соответствующее решению значение потока энтропии  . (20)
. (20) . (21)
. (21) и
и  равны
равны  соответственно, извлекаемая мощность P(qi) максимальна, когда
соответственно, извлекаемая мощность P(qi) максимальна, когда . (22)
. (22) , i, j=1, …, n [Вт/K]; коэффициенты теплопереноса для контактов преобразователя с подсистемами и резервуарами
, i, j=1, …, n [Вт/K]; коэффициенты теплопереноса для контактов преобразователя с подсистемами и резервуарами  , i=1, ..., n [Вт/K].
, i=1, ..., n [Вт/K]. по формуле (11) и значение температур контакта преобразователя с резервуарами по формуле (13);
по формуле (11) и значение температур контакта преобразователя с резервуарами по формуле (13); по формуле (12).
по формуле (12). , будем использовать для этого метод Ньютона:
, будем использовать для этого метод Ньютона: для системы (19), (9) относительно qi, i=1, …, m и
для системы (19), (9) относительно qi, i=1, …, m и 
 ;
; ;
; ; повторим итерацию до необходимой точности.
; повторим итерацию до необходимой точности. по формуле (16) и значение температур контакта
по формуле (16) и значение температур контакта  и извлекаемой мощности Ps*.
и извлекаемой мощности Ps*.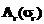 и
и  . Вычислим
. Вычислим 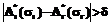 , перейдем к п. 4 с учетом
, перейдем к п. 4 с учетом  .
. и
и  .
. .
. и
и 