Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Конечные группы векторов для алгоритмов цифровой подписи
Аннотация:
Abstract:
| Автор: Молдовяну П.А. () - | |
| Ключевые слова: аутентификация информации, электронная цифровая подпись, векторы, конечные кольца, конечные группы |
|
| Keywords: , , , , |
|
| Количество просмотров: 10509 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
В современных информационных технологиях технической основой методов придания юридической силы электронным документам являются алгоритмы электронной цифровой подписи (ЭЦП), основанные на вычислительно сложных задачах в конечных алгебраических структурах с ассоциативной операцией [1]. Для повышения вычислительной эффективности в качестве примитивов алгоритмов ЭЦП были предложены конечные группы и поля, формируемые в векторных пространствах со специально определенной операцией умножения [2]. Показано, что при соответствующем выборе параметров векторного поля оно содержит подгруппу простого порядка, размер которого близок к размеру порядка поля. Конечные группы векторов являются нециклическими и содержат только подгруппы простого порядка относительно малого размера, что вносит ограничения на использование групп векторов в качестве примитива алгоритмов ЭЦП. В настоящей работе рассматриваются способ построения нециклических групп векторов, содержащих подгруппы большого простого порядка, и их применение для синтеза алгоритмов ЭЦП. Определение операции умножения в конечном векторном пространстве Конечное векторное пространство представляет собой множество элементов (векторов) вида a Рассмотрим построение мультипликативных групп в векторном пространстве, отличающихся различными вариантами задания операции умножения «´» векторов. Все варианты операции умножения векторов определяются в соответствии с [2] по общему правилу умножения каждой компоненты первого вектора-сомножителя с каждой компонентой второго вектора-сомножителя с сохранением в общем случае порядка следования компонент при их перемножении. Возникающие произведения двух базисных векторов заменяются на вектор e Формальное представление умножения векторов (a, b,…, c) и (x, y,…, z) имеет вид (a где каждое из произведений Таблицы умножения базисных векторов Таблицы составляются таким образом, чтобы операция умножения векторов была ассоциативной и коммутативной. Рассмотрим построение мультипликативных групп в векторном пространстве, заданном не над простым полем Таблица 1 Таблица умножения базисных векторов пятимерного векторного пространства
Таблица 2 Правила умножения базисных векторов для случая m=7
Синтез групп, содержащих подгруппы с большим размером простого порядка Рассмотрим подмножество {Z} m-мерных ненулевых векторов, координаты которых являются элементами кольца Векторы, для которых нет обратных значений, имеют следующий вид: N=(q1 p, q2 p, …, qm p), где q1Î{1, 2, …, k-1}; q2, q3, …, qmÎ{0, 1, 2, …, k-1} (нулевой вектор не входит в подмножество {Z}). Легко показать, что для таких векторов отсутствуют обратные значения. Действительно, из определенной операции умножения непосредственно вытекает, что у вектора V=N´X для произвольного вектора X каждая из координат делится на p, следовательно, V не может быть единичным вектором (1, 0, 0, …, 0). Число векторов N равно #{N}=(k-1)×km-1, следовательно, для значения порядка рассматриваемой группы векторов имеем значение, не превышающее W=p(k-1)×(kp)m-1-(k-1)×km-1=(k-1)×km-1(pm-1). Это значение достигается, если m делит p-1, а e является невычетом степени m по модулю p. Покажем, что это действительно так. Рассмотрим некоторый вектор Z=(a, b, ..., c), принадлежащий множеству {Z}. Перейдем от вектора Z к вектору Z¢=(a¢, b¢, ..., c¢), где a¢=a mod p, b¢=b mod p, ..., c¢=c mod p, который принадлежит при принятых условиях к векторному полю GF(pm) [2]. Поскольку Z¢¹(0, 0, …, 0), в векторном поле GF(pm) относительно неизвестного вектора X¢ существует решение векторного уравнения Z¢´X¢=E, где E=(1, 0, …, 0). Координаты вектора X¢=(x¢, y¢, ..., z¢) удовлетворяют системе сравнений следующего вида:
В этой системе коэффициенты При простом значении m, таком, что m½p-1, значение p можно выбрать так, что множитель q=m-1(pm-1+pm-1+…+p+1), содержащийся в разложении числа pm-1, будет простым. Таким образом, в построенной группе векторов содержится подгруппа простого порядка размера |q|=(m-1)|p|- –|m|»(m-1)|p|. Для построения алгоритмов ЭЦП требуется использовать подгруппы простого порядка Q размером не менее |Q|³160 бит. Для этой цели можно формировать нециклические группы m-мерных векторов, заданных над конечным кольцом
Синтез алгоритмов ЭЦП Рассмотрим возможный вариант обобщенной схемы ЭЦП, предполагая в нем использование циклической подгруппы векторов G¢, имеющей достаточно большой порядок q (|q|³160 бит). Например, в качестве G¢ может использоваться подгруппа максимально простого порядка, содержащаяся в нециклической группе G векторов размерности m=7, заданных над кольцом щееся невычетом степени m по модулю p. Подписывающий формирует свой открытый ключ Y в виде вектора Y=Gx, где G – вектор, являющийся генератором подгруппы G¢. Формирование подписи к сообщению M выполняется следующим образом: 1) выбрать случайное число k 2) используя некоторую криптографически стойкую хэш-функцию Fh, вычислить хэш-код h от сообщения M с присоединенным к нему вектором R: h=Fh(M, R). Значение h будет первым элементом ЭЦП; 3) вычислить второй элемент ЭЦП: s=xh+t mod q. Проверка подлинности подписи (h, s) состоит в следующем: 1) вычисляется вектор R¢=Yq-h ´Gs; 2) вычисляется значение h¢=Fh(M, R¢); 3) сравниваются значения h¢ и h; если h¢=h, ЭЦП признается подлинной. В заключение отметим, что в данной работе построены нециклические группы векторов, содержащие подгруппы простого порядка большого размера. Особенность построенной группы в том, что их координаты являются элементами конечного кольца Литература 1. Венбо Мао. Современная криптография. Теория и практика. М.–СПб–Киев: Издат. дом «Вильямс», 2005. 763 с. 2. Молдовян Н.А. Алгоритмы аутентификации информации в АСУ на основе полей векторов // Автоматика и телемеханика. 2008. 3. Бухштаб А.А. Теория чисел. М.: Просвещение, 1966. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2277&page=article |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Назад, к списку статей



 +b
+b +…+c
+…+c , где a, b,…, c – координаты, являющиеся элементами конечного простого поля GF(p);
, где a, b,…, c – координаты, являющиеся элементами конечного простого поля GF(p); 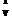 , где eÎGF(p) и
, где eÎGF(p) и  p, где p – простое число, а над конечным кольцом
p, где p – простое число, а над конечным кольцом 



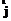





 .
. ,
,  , …,
, …, при неизвестных x¢, y¢, ..., z¢ определяются коэффициентами растяжения и координатами вектора Z¢. Известно, что если обе части сравнения и модуль делятся на одно и то же целое число, то обе части сравнения и модуль можно поделить на это число, получив эквивалентное сравнение ([3], теорема 128). Заменяя в этой системе сравнений a¢ на a, b¢ на b, ..., c¢ на c и умножая левую и правую части каждого сравнения и модуль на число k, получим систему сравнений, эквивалентную исходной. В векторном множестве {Z} полученной системе соответствует векторное уравнение Z´X=E¢, где E¢=(k, 0, …, 0)=kE. Очевидно, что вектор X=(kx¢, ky¢, ..., kz¢)=kX¢ является решением последнего уравнения, которое можно представить в виде kZ´X¢=kE, откуда следует Z´X¢=E, то есть X¢ является вектором, обратным вектору Z. Таким образом, при m½p-1 и e, являющемся невычетом степени m по модулю p, всем векторам множества {Z}, кроме векторов вида N, можно поставить в соответствие единственный обратный вектор, что требовалось показать. Теоретически определенное значение W=(k-1)×km-1(pm-1) подтверждается вычислительным экспериментом.
при неизвестных x¢, y¢, ..., z¢ определяются коэффициентами растяжения и координатами вектора Z¢. Известно, что если обе части сравнения и модуль делятся на одно и то же целое число, то обе части сравнения и модуль можно поделить на это число, получив эквивалентное сравнение ([3], теорема 128). Заменяя в этой системе сравнений a¢ на a, b¢ на b, ..., c¢ на c и умножая левую и правую части каждого сравнения и модуль на число k, получим систему сравнений, эквивалентную исходной. В векторном множестве {Z} полученной системе соответствует векторное уравнение Z´X=E¢, где E¢=(k, 0, …, 0)=kE. Очевидно, что вектор X=(kx¢, ky¢, ..., kz¢)=kX¢ является решением последнего уравнения, которое можно представить в виде kZ´X¢=kE, откуда следует Z´X¢=E, то есть X¢ является вектором, обратным вектору Z. Таким образом, при m½p-1 и e, являющемся невычетом степени m по модулю p, всем векторам множества {Z}, кроме векторов вида N, можно поставить в соответствие единственный обратный вектор, что требовалось показать. Теоретически определенное значение W=(k-1)×km-1(pm-1) подтверждается вычислительным экспериментом. (бит).
(бит).