Генетический алгоритм выбора доминантных признаков для нейронной сети
| Нигматуллина А.Н. (freebox_2006@bk.ru) - Казанский государственный технический университет им. А.Н. Туполева | |
| Ключевые слова: нейронная сеть, генетический алгоритм |
|
| Keywords: neural network, generic algorithm |
|
|
|
|
Автоматизация процесса формирования баз знаний – это актуальная задача, при решении которой широкое распространение получили технология KDD (Knowledge discovery from databases) и методы Data Mining, позволяющие извлекать скрытые закономерности из сырых данных. Наиболее популярны среди данных методов нейронные сети (НС). На этапе подготовки сырых данных для анализа одной из основных является задача выбора в них доминантных признаков, оказывающих наибольшее влияние на решение. Эта задача связана с формированием обучающих выборок для НС. Задача обучения НС заключается в подборе таких значений параметров НС, при которых ошибка была бы минимальной для данного обучающего множества. Вся информация о задаче содержится в наборе примеров. Поэтому качество обучения сети зависит от количества примеров в обучающей выборке и от того, насколько полно эти примеры описывают задачу. Для этого из исходных сырых данных необходимо сформировать выборки, отвечающие требованиям репрезентативности (отражения зависимости в генеральной совокупности) и представительности. Обучающая выборка A является представительной, если в заданном пространстве признаков и заданном классе решающих функций позволяет построить правило распознавания новых объектов (контрольной выборки Q) с ошибкой, не превышающей заданную величину. Применение генетических алгоритмов Генетические алгоритмы (ГА) относятся к классу методов случайного направленного поиска. Но в отличие от простого случайного поиска они основаны на принципах, заимствованных у природы, – генетической наследственности и естественного отбора [1]. Основная идея ГА – создание популяции особей, каждая из которых представлена в виде хромосомы. Любая хромосома – возможное решение рассматриваемой оптимизационной задачи. Для поиска лучших решений необходимо только значение целевой функции, или функции приспособленности особи, которая показывает, насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи. Хромосома состоит из конечного числа генов – что является генотипом объекта, то есть совокупностью его наследственных признаков. Эволюционный поиск ведется только на уровне генотипа. К популяции применяются основные биологические операторы: скрещивание, мутация, инверсия и др. Популяция постоянно обновляется при помощи генерации новых особей и уничтожения старых, каждая новая популяция становится лучше и зависит только от предыдущей [2]. Основное отличие ГА от традиционных методов поиска оптимумов состоит в том, что он с каждой эпохой улучшает оптимальное решение, но не гарантирует нахождение лучшего за конечный промежуток времени [1]. При применении ГА особое место занимает этап подготовки данных, от которого в наибольшей степени зависит успех работы алгоритма. Необходимость подготовки обусловлена тем, что выборка данных часто содержит случайные «выбросы», нетипичные и пропущенные значения, возможные ошибки ввода и т.д. ГА можно записать в виде кортежа: GA=, где P0 – исходная популяция; k – ее размер; n – количество генов в хромосоме; S, С, M – операторы отбора, кроссовера и мутации соответственно; F – функция приспособленности (фитнеса); t – критерий останова. Классическая схема ГА включает следующие шаги [2, 3]. 1. Задать начальный момент времени: t=0. Создать начальную популяцию из k особей (размер популяции): P0={A1 , A2 ,..., Ak}. 2. Рассчитать приспособленность каждой особи: F(Ai), i= 3. Выбрать из популяции две особи: Ai, Aj, i¹j. 4. Выполнить оператор кроссовера и мутации. В результате генерируется новая особь B (потомок). В некоторых модификациях алгоритма после скрещивания могут быть созданы несколько потомков (например два). 5. Поместить полученную хромосому (или несколько хромосом) в новую популяцию: Pt+1. 6. Выполнить оператор редукции, то есть сократить размер новой популяции до исходного размера. 7. Выполнить шаги, начиная с п. 3, k раз. 8. Увеличить номер текущей эпохи: t=t+1. 9. При срабатывании условия останова завершить работу, иначе перейти на шаг 2. Подготовка статистических данных Приведение данных к форме, пригодной для использования ГА, обязательно для эффективности данного процесса. Первым шагом является определение типов данных. Данные имеют различную природу и измеряются в различных количественных и качественных шкалах. Количественные данные получаются в результате измерения как в непрерывных, так и в дискретных шкалах. Качественные характеристики, как правило, закодированы, могут быть совершенно самостоятельными и независимыми друг от друга (номинальные признаки), а также составлять последовательность, условно выражаемую количественно (порядковые признаки). Бинарные признаки могут принимать одно из двух возможных значений. После определения типов данных формируется таблица, в первых столбцах которой записывают количественные и качественные характеристики, а в последних – бинарные. Далее необходимо выделить признаки, наиболее важные в контексте данного исследования и наиболее вероятно входящие в искомую зависимость. Для этого, как правило, используются статистические методы, основанные на применении корреляционного анализа [4], позволяющего быстро, хотя и приближенно, оценить влияние одного параметра на другой. Для поиска зависимостей между признаками, как правило, используются методы корреляционного анализа, в которых вычисляется коэффициент корреляции: rÎ[-1; 1], показывающий, в какой степени изменение значения одного признака влияет на изменение другого [4]: | r |≤0,25 – слабая корреляция; 0,25<| r |<0,75 – умеренная корреляция; | r |≥0,75 – сильная корреляция. Дальнейшая работа сводится к применению ГА для полученной таблицы. В результате работы алгоритма формируются обучающие выборки, которые подаются на вход НС, а после обучения НС получаются правила принятия решений. Эти правила проходят экспертную оценку. ГА выбора доминантных признаков Пусть имеется таблица 1 размера m´n, где si – полный набор признаков, Таблица 1 Статистические данные
Обозначим через R(d1, d2, …, dq, j) коэффициент множественной корреляции между признаками sj и ( Для выделения доминантных признаков необходимо рассчитать значения коэффициентов корреляции между всевозможными комбинациями кортежей, составленных из признаков si. При R(d1, d2, …, dq, j)>0,75 наблюдается сильная корреляция между признаками sj и ( Для решения этой задачи можно использовать метод полного перебора. Однако он неприемлем при больших значениях m и n. Для повышения эффективности процесса выделения доминантных признаков предложен следующий ГА. Примем за целевую функцию коэффициент множественной корреляции R(d1, d2, …, dq , j). В качестве хромосомы, описывающей особь, примем кортеж ( Обозначим через Q максимальное количество поколений; f – объем популяции; δ – вероятность мутации; Mass – динамический массив, элементами которого являются все вычисленные в процессе работы ГА коэффициенты множественной корреляции. Тогда алгоритм сводится к следующей последовательности шагов. 1. Генерируем случайным образом начальную популяцию, состоящую из f хромосом. 2. Для каждой из них вычисляем коэффициенты множественной корреляции Rb(d1, d2, …, dq , j) (значения целевой функции), 3. Полученные значения Rb(d1, d2, …, dq, j) записываем в массив Mass. 4. Осуществляем селекцию турнирным методом, разбивая популяцию на подгруппы по 2 хромосомы, и производим детерминированный выбор хромосомы с наиболее высоким значением целевой функции. 5. Выполняем одноточечное скрещивание хромосом, отобранных на предыдущем шаге. К полученным потомкам применяем оператор одноточечной мутации с вероятностью δ. 6. Для каждого из потомков вычисляем целевую функцию, которую записываем в массив Mass. 7. В новое поколение попадают f хромосом с наибольшим значением целевой функции. 8. Если превышено указанное количество поколений Q или наблюдается малая разница значений целевой функции лидеров последних h поколений, то прерываем процесс, иначе возвращаемся к шагу 3. Таким образом, получен массив Mass, состоящий из всех вычисленных в процессе работы ГА коэффициентов множественной корреляции. Причем с каждым новым поколением массив пополнялся новыми элементами R(d1, d2, …, dq, j), значения которых больше или равны предыдущим. Из полученного массива остается выбрать все R(d1, d2, …, dq , j)>0,75 и сформировать соответствующие им доминантные признаки. ГА формирования обучающих выборок для НС Пусть имеется таблица 2 размера m´n, где si – возможные входы, а tj – возможные выходы для НС; Таблица 2 Статистические данные
Обозначим через R(d1, d2, …, dq, j) коэффициент множественной корреляции между признаками tj и ( Чтобы определить количество входов для конкретного выхода tj НС, необходимо просчитать значения коэффициентов корреляции между признаком tj и всевозможными комбинациями кортежей, составленных из признаков si. При R(d1, d2, …, dq, j)>0,75 наблюдается сильная корреляция между признаками tj и ( Для решения этой задачи можно использовать метод полного перебора. Однако он неприемлем при больших значениях m и n. Для повышения эффективности процесса формирования обучающих выборок для НС предложен следующий ГА. Примем за целевую функцию коэффициент множественной корреляции R(d1, d2, …, dq , j). В качестве хромосомы, описывающей особь, примем кортеж ( Обозначим через Q максимальное количество поколений; f – объем популяции; δ – вероятность мутации; Mass – динамический массив, элементами которого являются все вычисленные в процессе работы ГА коэффициенты множественной корреляции. Тогда алгоритм сводится к следующей последовательности шагов. 1. Генерируем случайным образом начальную популяцию, состоящую из f хромосом. 2. Для каждой из них вычисляем коэффициенты множественной корреляции Rb(d1, d2, …, dq , j) (значения целевой функции), 3. Полученные значения Rb(d1, d2, …, dq, j) записываем в массив Mass. 4. Осуществляем селекцию турнирным методом, разбивая популяцию на подгруппы по 2 хромосомы, и производим детерминированный выбор хромосомы с наиболее высоким значением целевой функции. 5. Производим одноточечное скрещивание хромосом, отобранных на предыдущем шаге. К полученным потомкам применяем оператор одноточечной мутации с вероятностью δ. 6. Для каждого из потомков вычисляем целевую функцию, которую записываем в массив Mass. 7. В новое поколение попадают f хромосом с наибольшим значением целевой функции. 8. Если превышено указанное количество поколений Q или наблюдается малая разница значений целевой функции лидеров последних h поколений, то прерываем процесс, иначе возвращаемся к шагу 3. Итак, получен массив Mass, состоящий из всех вычисленных в процессе работы ГА коэффициентов множественной корреляции. Причем с каждым новым поколением массив пополнялся новыми элементами R(d1, d2,…, dq, j), значения которых больше или равны предыдущим. Из полученного массива остается выбрать все R(d1, d2, …, dq, j)>0,75 и сформировать соответствующие им обучающие выборки. В большинстве случаев получаемые при помощи ГА обучающие выборки являются оптимальными для НС, что позволяет использовать его самостоятельно. Для проверки работы ГА использованы данные клинического нейроортопедического, рентгенокомпьютернотомографического обследования 230 женщин в возрасте от 15 до 92 лет и 180 мужчин в возрасте от 16 лет до 81 года с различными синдромами поясничного остеохондроза. Контрольную группу составили 20 женщин от 20 до 70 лет и 20 мужчин от 17 до 73 лет. Клиническое нейроортопедическое обследование проведено по методике В.П. Веселовского, Я.Ю. Попелянского (http://www.kazanmedacademy.ru/ m02_001_005.html). Рентгеновская компьютерная томография проводилась на томографе SOMATOM AR.HP spiral фирмы SIEMENS при сканировании с шагом 3/3 мм. Изучены количественные и качественные характеристики состояния структур позвоночно-двигательных сегментов, собственных мышц позвоночника и паравертебральных мышц на уровне LIII- SI по методике М.А. Подольской, З.Ш. Нуриева (см. ссылку выше). Для получения обучающих выборок измерено более 500 000 количественных и качественных значений признаков течения поясничного остеохондроза по 822 параметрам. При помощи нечеткой НС проанализированы возможные варианты зависимости различных качественных и количественных признаков. В результате обучения НС на более чем 100 обучающих выборках было получено свыше 500 правил, значимость которых подтверждена экспертами – специалистами-вертеброневрологами высокой квалификации. Литература 1. Паклин Н.Б. Адаптивные модели нечеткого вывода для идентификации нелинейных зависимостей в сложных системах: дис. … к-та техн. наук. Ижевск, 2004. 162 с. 2. Батищев Д.И. Генетические алгоритмы решения экстремальных задач: учеб. пособ.; под ред. Я.Е. Львовича. Воронеж, 1995. 3. Осовский С. Нейронные сети для обработки информации; пер. с польск. И.Д. Рудинского. М.: Финансы и статистика, 2002. 344 с. 4. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикл. программ Statistica. М.: МедиаСфера, 2003. 312 с. |
http://swsys.ru/index.php?id=2301&lang=.docs&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Интеллектуальная информационная система для решения задач прогнозирования неисправностей вагонного оборудования на железнодорожном транспорте
- Обнаружение аномалий сетевого трафика методом глубокого обучения
- Интеллектуальная система прогнозирования на основе методов искусственного интеллекта и статистики
- Алгоритм детектирования объектов на фотоснимках с низким качеством изображения
- Генетический алгоритм автоматизированного проектирования подготовительных переходов ковки

 .
. . Требуется из данных признаков выделить доминантные.
. Требуется из данных признаков выделить доминантные. ,
,  , …,
, …,  ), где все значения dq и j различны, j,dqÎ{1, 2, …, n}, j,q≤n.
), где все значения dq и j различны, j,dqÎ{1, 2, …, n}, j,q≤n.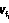 ,
, , …,
, …,  ),
),  Î{0, 1, 2},
Î{0, 1, 2}, . Если все Rb(d1, d2, …, dq , j)>0,75, возвращаемся на шаг 1.
. Если все Rb(d1, d2, …, dq , j)>0,75, возвращаемся на шаг 1. ,
, 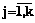 . Требуется из данных признаков сформировать обучающие выборки для НС.
. Требуется из данных признаков сформировать обучающие выборки для НС.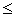 p, dq¹dl.
p, dq¹dl. ,
, ,
,  ,
,  ,…,
,…, ),
),  ,
, Î{0,1}. Здесь минимум два значения
Î{0,1}. Здесь минимум два значения 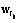 , кроме одного, равны нулю. Если
, кроме одного, равны нулю. Если