Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Конструирование алгоритмов синтеза индуктивных моделей сложных систем
Аннотация:Статья посвящена исследованию особенностей конструирования индуктивных алгоритмов синтеза моделей сложных систем на основании объединения нескольких моделирующих алгоритмов или отдельных их компонент в новые схемы, которые уже имеют новые свойства и обеспечивают более высокий уровень адекватности результирующих моделей в сравнении с алгоритмами, положенными в их основу.
Abstract:The article is devoted to research of features of constructing of inductive algorithms of synthesis of models of the difficult systems on the basis of association of a few modeling algorithms, or separate their component, in new schemes, which have a new characteristics and provide more high level of adequacy of resulting models by comparison to algorithms which were fixed in their basis.
| Авторы: Колос П.А. (dr_peter@cdu.edu.ua) - Черкасский национальный университет им. Богдана Хмельницкого, Украина | |
| Ключевые слова: адекватность результирующей модели, конструктор алгоритмов синтеза моделей, метод степаненко, метод группового учета аргументов, методы эвристической самоорганизации, индуктивное моделирование |
|
| Keywords: adequacy of resulting model, constructor of models synthesis algorithms, method of Stepanenkо, group method of data handling, methods of heuristic selforganization, inductive design |
|
| Количество просмотров: 13814 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
При исследовании значительного числа объектов наиболее распространенными остаются имитационные методы моделирования, основанные на определении причинно-следственных связей и являющиеся детерминистическими. Использование детерминистических подходов дает приемлемые результаты при моделировании относительно простых систем. Эти системы достаточно исследованы, и считается, что причинно-следственные связи в них отслежены с удовлетворительной достоверностью. В случаях, когда имитационная модель разрешает предусмотреть поведение исследуемого объекта с высокой точностью, использование этих моделей оправданно и целесообразно [1]. Исследование сложных систем показало, что детерминистические модели чрезвычайно сложные и работают с низкой эффективностью. В таких случаях целесообразно использовать индуктивные модели, квалифицированные как алгебраические. Модели этого класса, основанные на принципах селекции, эволюции и адаптации, носят название методов эвристической самоорганизации [1]. К ним можно отнести разного рода эволюционные алгоритмы, индуктивные методы моделирования, нейросети, генетические алгоритмы и др. Тем не менее, на практике довольно трудно создать адекватную модель сложного объекта при использовании только одного метода индуктивного моделирования. Обычно необходимо объединять современные методы и технологии эвристической самоорганизации, выполнять рециркуляцию, применять методы многоуровневого моделирования и т.п. [2]. Таким образом, есть необходимость в разработке технологии, которая, базируясь на современных методах индуктивного моделирования, позволяла бы сгенерировать новый алгоритм синтеза соответствующей модели, обеспечивающий лучшее решение для исследуемой системы. Разработано много CASE-средств и специализированных математических программных пакетов, которые позволяют использовать и разрабатывать методы и технологии имитационного и индуктивного моделирования. Среди последних можно выделить популярный программный продукт для выполнения математических расчетов MathLab. Система MathLab имеет мощный инструментарий для решения разнообразных математических задач, в том числе и задач математического моделирования. Развитыми средствами MathLab можно реализовать методы эвристической самоорганизации и дальше сгенерировать модель исследуемого объекта. Тем не менее, данная система не является совершенной и имеет существенные недостатки. Во-первых, в ней отсутствуют встроенные сервисы, которые разрешали бы использовать уже готовые технологии и строить индуктивные модели, не беспокоясь о структуре того или иного алгоритма. Во-вторых, нет единой нотации создания и объединения алгоритмов эвристической самоорганизации. В-третьих, система MathLab довольно сложна в использовании: создавать новые прибавления, реализуя современные алгоритмы индуктивного моделирования, может только опытный пользователь. Другой подход – использование общецелевого языка визуального моделирования UML (Universal Modeling Language). Язык UML – одновременно и простое, и мощное средство моделирования, которое может эффективно использоваться для построения концептуальных, логических и графических моделей сложных систем разного целевого назначения. Конструктивное использование языка UML базируется на понимании общих принципов моделирования сложных систем и особенностей процесса объектно-ориентированного анализа и проектирования в частности. Выбор средств для построения моделей сложных систем определяет те задачи, которые могут быть решены с использованием данных моделей [3]. Хотя язык UML и можно применить при разработке моделей сложных систем эвристическими методами самоорганизации, тем не менее, главное назначение данной технологии – моделирование сложных информационных систем и разработка программных продуктов корпоративного назначения. Среди CASE-средств, реализующих язык UML, можно выделить Rational Rose, Visual UML, Power Designer и т.п. Основное назначение этих систем – автоматизированное объектно-ориентированное программирование. Используя подобный программный комплекс, можно спроектировать информационную программную систему, сгенерировать программный код, скомпоновать образованные модули и получить готовый программный продукт. Вмешательство программиста в непосредственное написание программного кода минимальное. Таким образом, использование методов эвристической самоорганизации, построение модели сложной системы при использовании языка UML возможны только в виде реализации программного модуля. Данный подход теряет гибкость; так как UML имеет довольно высокий уровень абстракции и первоочередная ориентация этого языка моделирования – корпоративная сфера, разработка такого программного модуля требует от пользователя детальных знаний алгоритма функционирования каждого метода индуктивного моделирования и разработки детальных диаграмм в соответствии с нотацией UML. Такой подход неудобен и требует больших временных затрат. Объект авторского исследования – технология индуктивного моделирования, которая разрешает генерировать алгоритмы синтеза моделей сложных систем, базируясь на современных методах эвристической самоорганизации. Подобный подход позволял бы создать алгоритм, дающий возможность синтезировать индуктивную модель, наиболее адекватно описывающую исследуемый сложный объект. Задача автора – исследование особенностей создания и программной реализации технологии конструирования алгоритмов синтеза сложных систем. Разработка системы конструирования алгоритмов синтеза индуктивных моделей сложных систем имеет ряд особенностей, связанных с определением необходимого инструментария для создания и настройки схем алгоритмов и минимального набора элементов для конструирования. Конструктор алгоритмов синтеза моделей должен базироваться на определенном наборе современных методов эвристической самоорганизации, применение которых для генерирования индуктивных моделей объектов исследования реализуется через набор определенных компонент для создания схем алгоритмов. Необходимые компоненты сначала прибавляются на схему, а потом устанавливаются связи, обеспечивающие корректное взаимодействие компонент. Результат обхода схемы – создание модели определенного сложного объекта исследования или построение прогноза изменений определенных параметров моделированной системы. На первом этапе разработки конструктора каждый из методов моделирования был реализован в виде отдельного компонента схемы алгоритма. То есть существовали компонент создания модели определенным методом эвристической самоорганизации и компонент вычисления модели, созданной этим методом, другими словами, компонент прогнозирования. Пример схемы алгоритма, представленный на рисунке 1, объединяет два метода индуктивного моделирования – метод группового учета аргументов (МГУА) и метод Степаненко.
Первичные данные получены из Центра медицинской статистики (www.medstat.com.ua) Минздрава Украины, БД «Здоровье для всех. Украина» по состоянию на август 2006 года. Результаты моделирования показали, что среднеквадратическое отклонение (СКО) по МГУА – 3,91; по методу Степаненко – 4,4; по схеме, последовательно объединяющей эти два метода, – 3,6 (см. рис. 1). Очевидно, что МГУА дает довольно неплохие результаты, метод Степаненко худшие, а объединение этих методов обеспечивает минималь- ное СКО.
Этот простой пример показывает, как быстро и удобно, пользуясь набором компонентов, можно создать технологию моделирования, наиболее подходящую для решения конкретной задачи моделирования сложного объекта. Такая реализация конструктора алгоритмов синтеза индуктивных моделей дает возможность получать сложные схемы с использованием разных методов моделирования, причем образовывать циклы и использовать результаты моделирования по одному методу как входной поток данных для другого метода. Тем не менее, в этом случае невозможно вмешаться в процесс функционирования метода построения модели, изменять этапы моделирования и комбинировать особенности нескольких методов эвристической самоорганизации. Таким образом, для обеспечения большей гибкости при конструировании той или иной схемы алгоритма синтеза модели лучшим подходом будет реализация разных методов моделирования в виде не одного компонента схемы, а набора компонент, обеспечивающего работу данного метода. Это второй этап развития системы конструирования алгоритмов синтеза моделей сложных систем. Для примера рассмотрим конструирование индуктивного алгоритма на основе компонентов метода Степаненко и МГУА (рис. 2). Создание модели по этому алгоритму предусматривает несколько этапов: разбивка таблицы первичного описания на обучающую и проверяющую последовательности, создание первого ряда селекции, обучение модели, генерирование следующего ряда селекции, вычисление погрешностей, проверка условия завершения процесса моделирования. Необходимо, чтобы каждому этапу отвечал определенный отдельный компонент схемы. Такой подход даст возможность модифицировать метод и осуществить нужный план создания модели объекта исследования. Кроме того, на каждом этапе генерирования ряда селекции методом МГУА выполняются генерирование и вычисление модели методом Степаненко, объединение данных и передача данных моделирования на новый ряд селекции МГУА. Доказательством того, что такой подход лучший и обеспечивает образование наиболее адекватной модели сложного объекта, является схема (рис. 2) с экспериментальными данными. Результаты моделирования показали, что СКО по модели, полученной по схеме, изображенной на рисунке 2, составило 3,3. Очевидно, что такой подход обеспечивает еще более низкую погрешность моделирования. Таким образом, система конструирования алгоритмов синтеза моделей сложных систем обеспечивает возможность создания наиболее адекватной модели объектов мониторинга окружающей среды при условии использования и комбинирования нескольких современных методов эвристической самоорганизации. Экспериментально подтверждена эффективность использования конструктора алгоритмов синтеза моделей, спроектированного по вышеописанным принципам. Определено, что интеграция методов конструирования алгоритмов моделирования на уровне компонентов может быть более эффективной, чем объединение на уровне алгоритмов. Дальнейшие исследования будут проводиться в направлении определения закономерностей, которые позволяют обеспечивать максимальные системные свойства в моделях, сгенерированных по описанным принципам. Литература 1. Ивахненко А.Г. Индуктивный метод самоорганизации моделей сложных систем. Киев: Наук. Думка, 1981. 296 с. 2. Голуб С.В. Багаторівневе моделювання в технологіях моніторингу оточуючого середовища. Монографія. Черкаси: Вид. від. ЧНУ імені Богдана Хмельницького, 2007. 220 с. 3. Леоненков А.В. Самоучитель UML. СПб: БХВ-Петербург, 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2302&page=article |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Назад, к списку статей



 Исследование особенностей данного подхода проводилось при моделировании зависимости уровня заболеваемости населения Черкасской области туберкулезом и разными видами раковых заболеваний от образа жизни человека и уровня загрязнения окружающей среды. Моделируемая функция – количество случаев заболевания на 10 тысяч человек населения. Параметры моделирования – образ жизни человека и уровень загрязнения окружающей среды.
Исследование особенностей данного подхода проводилось при моделировании зависимости уровня заболеваемости населения Черкасской области туберкулезом и разными видами раковых заболеваний от образа жизни человека и уровня загрязнения окружающей среды. Моделируемая функция – количество случаев заболевания на 10 тысяч человек населения. Параметры моделирования – образ жизни человека и уровень загрязнения окружающей среды.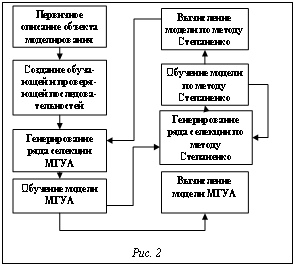 Схема алгоритма отражает технологию создания индуктивной модели. В этом примере объект моделирования представляется набором данных, которые инкапсулируются в компоненте первичного описания объекта. На основе данных генерируется модель методом Степаненко. Следующий компонент вычисляет новообразованную модель, прибавляет результаты прогнозирования к таблице первичного описания и передает их на вход компоненту моделирования по методу МГУА.
Схема алгоритма отражает технологию создания индуктивной модели. В этом примере объект моделирования представляется набором данных, которые инкапсулируются в компоненте первичного описания объекта. На основе данных генерируется модель методом Степаненко. Следующий компонент вычисляет новообразованную модель, прибавляет результаты прогнозирования к таблице первичного описания и передает их на вход компоненту моделирования по методу МГУА.