Граничные условия локальной задачи в методе подсеток
| Мельниченко Н.С. (nikita.melnichenko@gmail.com) - Московский государственный университет им. М.В. Ломоносова | |
| Ключевые слова: оценка погрешности, граничные условия, метод подсеток, многоточечная аппроксимация, задача фильтрации |
|
| Keywords: error estimation, boundary conditions, subgrid method, multipoint approximation, fluid filtration |
|
|
|
|
При пространственной аппроксимации задачи фильтрации вязкой сжимаемой многофазной смеси в пористой среде в трехмерной области [1] методом конечных объемов возникает проблема приближения потока В наиболее часто используемой двухточечной аппроксимации этот поток приближают по значениям в двух соприкасающихся блоках, содержащих S, однако это приводит к большой погрешности в случае неортогональной сетки [2] и является причиной существенной ошибки в результатах расчета гидродинамической модели. Современные программные комплексы моделирования предлагают возможность использовать различные многоточечные методы, которые позволяют сократить эту погрешность за счет большего количества точек в окрестности грани и, как следствие, увеличения времени расчета. В данной статье рассмотрены авторская разработка многоточечного метода подсеток [3] и способ выбора его параметров, при котором погрешность приближения потока остается на низком уровне. При вычислении потока в методе подсеток рассматривается каждая вершина V грани S, строится область взаимодействия W(V), состоящая из всевозможных базовых тетраэдров PMEV, где E – центр содержащего узел V ребра; M – барицентр содержащей его грани; P – барицентр содержащего ее блока. Каждый из этих тетраэдров разбивается на меньшие тетраэдры, в результате W(V) разбита подсеткой. Методом конечных элементов на ней решается задача divKÑu=0, и полученное решение используется для определения потока через S∩W(V), части полного потока через S. Необходимо задать граничные условия локальной задачи на подсетке таким образом, чтобы погрешность приближения потока была как можно ниже. Составление граничных условий. Для вершины V, лежащей внутри расчетной области, граница области взаимодействия W=W(V) оказывается состоящей из треугольников PME. Значение в точке P считаем известным. Построим приближенные значения в точках M и E (далее будем обозначать через
где Обозначим
Тогда для ортонормированного базиса
Матрицы Ai в силу положительной определенности матриц Ki являются невырожденными. Пусть точка DÎp, тогда
Отсюда
Таким образом, получено ограничительное уравнение Для получения приближения Ñu в блоке, содержащем L, используем полученный результат для случая, когда p является плоскостью некоторой грани блока, а P1, P2 – барицентрами блоков, содержащих эту грань. Допустим, найдены такие три соседних блока, что векторы
позволяющую определить вектор
Значения внутри треугольника определим линейной интерполяцией по значениям в точках P, M и E. При вычислениях с ограниченной точностью условие линейной независимости векторов
где áv1,…,vn ñ – объем n-мерного параллелепипеда, натянутого на векторы; c1, c2>0 – константы; h – диаметр множества точек текущей области взаимодействия. В случаях, близких к вырожденным, когда базис Порядок аппроксимации потока. Найдем порядок аппроксимации потока для грани, имеющей вершинами внутренние узлы сетки, при приближении методом подсеток в однородном изотропном случае. Не нарушая общности, будем считать, что тензор равен единичному во всей области. Предположим, что в некоторый момент точно известны значения функции u в центрах блоков, а диаметр области взаимодействия ра- вен h. Лемма 1. При принятых предположениях значения функции uÎC2(W), вычисленные на гранях PME базовых тетраэдров, определены с точностью O(h2). Доказательство. Рассмотрим вычисление приближения градиента
Заметим, что
На основании формулы Тейлора имеем Тогда получим
где Значения во всех точках треугольника PME были получены линейной интерполяцией по значениям в его вершинах, а значит, не отличаются от них более чем на O(h2). В силу принципа максимума для рассматриваемой дискретной задачи [4] приближение uhÎUh функции uÎC2(W) отличается от нее в узлах подсетки на O(h2). Рассмотрим поток через поверхность Теорема 1. Пусть все базовые тетраэдры области взаимодействия W удовлетворяют Õ-критерию. Тогда при принятых ранее предположениях порядок аппроксимации потока через поверхность s при расчете с помощью метода подсеток равен mes(s)O(h) для функции uÎC2(W). Доказательство. Значения функции в узлах подсетки при расчете с помощью метода подсеток определены с точностью O(h2). Рассмотрим грань l подсетки, содержащуюся в рассматриваемой грани S сетки. Тетраэдры t1 и t2, содержащие ее, подобны своим базовым тетраэдрам с некоторым постоянным коэффициентом v [3] и удовлетворяют Õ-критерию с параметром hv-1. Как видно из доказательства леммы 1, порядок приближения Таким образом, теорема показывает, что при естественных ограничениях (Õ-критерий позволяет исключить из рассмотрения вырожденные случаи) в однородном изотропном случае метод подсеток дает приемлемую аппроксимацию потока. Проведенные численные эксперименты [5] на различных тестовых и реальных задачах с помощью программного комплекса гидродинамического моделирования, в составе которого был реализован данный многоточечный метод, подтверждают аналитические выводы и показывают, что данный подход так же корректно работает и для неоднородной анизотропной среды. Литература 1. Aziz K., Settari A. Petroleum Reservoir Simulation. London: Applied Science Publishers, 1979. 2. Aavatsmark I. An Introduction to Multipoint Flux Approximations for Quadrilateral Grids // Computational Geosciences. 2002. № 6, № 3–4. С. 405–432. 3. Богачев К.Ю., Мельниченко Н.С. О пространственной аппроксимации методом подсеток для задачи фильтрации вязкой сжимаемой жидкости в пористой среде // Вычислительные методы и программирование. 2008. № 9. С. 191–199. 4. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987. 5. Богачев К.Ю., Мельниченко Н.С., Шелков В.Г. Применение метода подсеток для гидродинамического моделирования в анизотропной среде на нерегулярных сетках // Нефтех. 2008. № 4. С. 8–12. |
http://swsys.ru/index.php?id=2303&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

 через грань S сетки, блоки которой – это стыкующиеся шестигранники, где K=KT>0 – тензор абсолютной проницаемости; kr,l – относительная проницаемость фазы l; ml – вязкость фазы l; pl – давление в фазе l; gl=grl, rl – плотность фазы l; d – функция глубины;
через грань S сетки, блоки которой – это стыкующиеся шестигранники, где K=KT>0 – тензор абсолютной проницаемости; kr,l – относительная проницаемость фазы l; ml – вязкость фазы l; pl – давление в фазе l; gl=grl, rl – плотность фазы l; d – функция глубины;  – нормаль к грани S.
– нормаль к грани S. любую из этих точек). Рассмотрим вспомогательную задачу. Пусть функция u задана и непрерывна на всем пространстве, которое разделено на полупространства Q1 и Q2 плоскостью p. В Q1 заданы точка P1, значение u1=u(P1) и тензор проницаемости K1, в Q2 – точка P2, значение u2=u(P2), тензор K2. Известно, что функция u линейна в каждом полупространстве и имеет место равенство потоков через некоторую поверхность sÌp:
любую из этих точек). Рассмотрим вспомогательную задачу. Пусть функция u задана и непрерывна на всем пространстве, которое разделено на полупространства Q1 и Q2 плоскостью p. В Q1 заданы точка P1, значение u1=u(P1) и тензор проницаемости K1, в Q2 – точка P2, значение u2=u(P2), тензор K2. Известно, что функция u линейна в каждом полупространстве и имеет место равенство потоков через некоторую поверхность sÌp: , (1)
, (1) .
.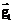 , а
, а  – через
– через  . В силу линейности u для любых точек D1, D2Îp верно
. В силу линейности u для любых точек D1, D2Îp верно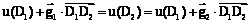 .
. плоскости p имеют место равенства
плоскости p имеют место равенства  , i=1, 2. Поскольку
, i=1, 2. Поскольку  являются константами и тензор проницаемости симметричен, уравнение (1) запишется как
являются константами и тензор проницаемости симметричен, уравнение (1) запишется как 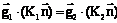 . Таким образом, связь градиентов
. Таким образом, связь градиентов  , где
, где i=1, 2.
i=1, 2.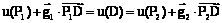 .
.
 .
. , где
, где 
 . Отметим, что значение этого вектора получается не зависящим от D, а в случае K1=K2 оператор
. Отметим, что значение этого вектора получается не зависящим от D, а в случае K1=K2 оператор  является единичным и
является единичным и  .
. ,
, 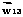 ,
, 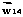 оказались линейно независимыми. В этом случае получим систему уравнений
оказались линейно независимыми. В этом случае получим систему уравнений , j=2, 3, 4, (2)
, j=2, 3, 4, (2) . Искомые значения могут быть вычислены по формуле
. Искомые значения могут быть вычислены по формуле . (3)
. (3) не является достаточным для получения удовлетворительного результата. Пусть векторы v1, …, vn удовлетворяют Õ-критерию, если
не является достаточным для получения удовлетворительного результата. Пусть векторы v1, …, vn удовлетворяют Õ-критерию, если ,
,  , 1≤i≤n,
, 1≤i≤n, функции u в центре P1 некоторого блока. Положим, группа соседних блоков с центрами P2, P3, P4 такова, что векторы
функции u в центре P1 некоторого блока. Положим, группа соседних блоков с центрами P2, P3, P4 такова, что векторы 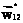 ,
,  ,
,  для решения системы (2), получим представление
для решения системы (2), получим представление  . (4)
. (4)

 , откуда, учитывая, что
, откуда, учитывая, что  в однородном случае,
в однородном случае, 
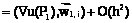 .
. (5)
(5) . Приближение значения u(L) равно
. Приближение значения u(L) равно 
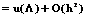 .
.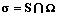 . Пусть тетраэдр ABCD удовлетворяет Õ-критерию, если векторы
. Пусть тетраэдр ABCD удовлетворяет Õ-критерию, если векторы  ,
,  ,
,  удовлетворяют Õ-критерию.
удовлетворяют Õ-критерию. по формуле (5) равен O(h), учитывая, что значения в вершинах тетраэдра известны с точностью O(h2). Из этого следует, что поток через треугольник l вычислен с точностью mes(l)O(h), откуда полный поток определен с точностью mes(s)O(h).
по формуле (5) равен O(h), учитывая, что значения в вершинах тетраэдра известны с точностью O(h2). Из этого следует, что поток через треугольник l вычислен с точностью mes(l)O(h), откуда полный поток определен с точностью mes(s)O(h).