Общая теория систем начинается с определения системы как комплекса взаимодействующих компонентов, формирующих организованное целое. Такое определение естественным образом приводит к удобному и эффективному моделированию самых разнообразных систем (физических, как природных, так и искусственных, биологических, социальных) на языке теории графов (сетей), когда компоненты суть вершины, а их взаимодействия – связывающие эти вершины ребра.
В последнее десятилетие теория сложных сетей проявила себя как один из универсальных методов исследования сложных систем. Сети – всё вокруг нас, и мы сами как индивидуумы являемся элементами сети социальных отношений различных видов, а как биологические системы – результатом сети биохимических реакций. Сети могут быть материальными объектами в евклидовом пространстве (энергетические сети, Интернет, автомагистрали, метро или нейронные сети) или же объектами, определенными в абстрактном пространстве (WWW, сети знакомств или сотрудничества между людьми).
Существенные достижения в исследовании сложных сетей обусловлены несколькими обстоятельствами. Во-первых, компьютеризация сбора данных во всех сферах привела к появлению больших БД по топологии разнообразных сетей реального мира. Во-вторых, расширившиеся вычислительные возможности позволили изучать сети, содержащие миллионы вершин, и исследовать аспекты, которые не могли быть рассмотрены прежде. В-третьих, медленное, но значимое стирание границ между дисциплинами открыло исследователям из разных предметных областей доступ к разнообразным БД, что позволило обнаружить универсальные свойства сложных сетей.
Изучение структуры сетей реального мира показало, что сложные сети разделяются по форме распределения степеней на случайные (сети Эрдеша–Реньи), мало-мировые (сети Ваттса–Строгатца) и масштабно-инвариантные (сети Барабаси–Альберт (БА)) [1]. Масштабно-инвариантные сети характеризуются распределением степеней, которое подчиняется степенному закону  , где
, где 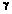 – показатель степени. В отличие от случайных и мало-мировых масштабно-инвариантные сети имеют сильно неоднородную структуру. Анализ топологии сетей реального мира показал, что многие из искусственных систем характеризуются степенным распределением.
– показатель степени. В отличие от случайных и мало-мировых масштабно-инвариантные сети имеют сильно неоднородную структуру. Анализ топологии сетей реального мира показал, что многие из искусственных систем характеризуются степенным распределением.
Для объяснения феномена масштабно-инвариантных сетей БА была предложена модель растущих сетей, ставшая в теории сложных сетей базовой. В основе БА-модели лежат два механизма: рост и предпочтительное присоединение, а именно, сети растут за счет добавления новых вершин; вновь поступившая в сеть вершина соединяется с вершинами, уже присутствующими в сети, в соответствии с принципом предпочтительного присоединения (то есть вероятность соединения с вершиной i пропорциональна ее степени ki:  ). Модель БА приводит к сети, распределение степеней которой подчиняется степенному закону
). Модель БА приводит к сети, распределение степеней которой подчиняется степенному закону  . Несмотря на то, что БА-модель объясняет основные особенности большей части сетей реального мира (степенной характер распределения степеней, динамику роста степеней отдельных узлов и т.д.), строго фиксированное значение показателя g=3 является существенным недостатком модели. Так, анализ сетей реального мира показал, что значение показателя степени
. Несмотря на то, что БА-модель объясняет основные особенности большей части сетей реального мира (степенной характер распределения степеней, динамику роста степеней отдельных узлов и т.д.), строго фиксированное значение показателя g=3 является существенным недостатком модели. Так, анализ сетей реального мира показал, что значение показателя степени  [1, 2]. Очевидно, что эта особенность связана с присутствием дополнительных механизмов роста сетей. Обобщенная модель предполагает следующие механизмы роста сети.
[1, 2]. Очевидно, что эта особенность связана с присутствием дополнительных механизмов роста сетей. Обобщенная модель предполагает следующие механизмы роста сети.
1. Добавление ребер: с вероятностью r (0£r£1) в сеть добавляется m новых ребер, для каждого из которых одна из вершин выбирается случайным образом, а другая – с вероятностью  .
.
2. Добавление вершин: с вероятностью 1–r в сеть поступает новая вершина, которая соединяется с вершинами, уже присутствующими в сети, m ребрами опять-таки в соответствии с принципом предпочтительного присоединения.
Несколько позже был предложен еще целый набор дополнительных механизмов, которые могут затрагивать как собственно процесс роста (пересвязывание ребер, слияние узлов и т.д.), так и принцип предпочтительного присоединения (нелинейное предпочтительное присоединение, ускоренный рост, старение узлов и т.д.) [1, 2]. Исследования показали, что все эти механизмы приводят к сетям с нарушенной масштабно-инвариантной топологией.
При дальнейшем изучении сетей реального мира выявилось, что может нарушаться и принцип глобального действия предпочтительного присоединения. Так, исследования Международной торговой сети (WTW) показали, что при росте сети механизм предпочтительного присоединения действует, но не глобально, а локально [3]. Последнее означает, что при добавлении в сеть новой вершины она может соединиться только с вершинами некоторой подсети (например, не с произвольными торговыми организациями, а с расположенными в определенном регионе). Такую подсеть в дальнейшем и будем называть локальным миром добавляемой вершины.
В данной работе представлены результаты исследования локально-мировых сетей.
Модели формирования растущих локально-мировых сетей
Определим алгоритм формирования растущих локально-мировых сетей как дальнейшее обобщение модели масштабно-инвариантой сети БА. При таком подходе процесс формирования локально-мировой растущей сети можно описать следующим образом.
1. Рост. Генерация сети начинается с небольшого числа m0 изолированных узлов, в каждый момент t к сети добавляется новый узел, который должен быть связан с уже существующими вершинами m ребрами.
2. Локальное предпочтительное присоединение. В каждый момент t перед соединением нового узла с m узлами, уже присутствующими в сети, формируется локальный мир. Ребра добавляются между новой вершиной и m вершинами локального мира. Таким образом, вероятность связывания некоторого узла i локального мира с новым узлом отобразим как  .
.
3. Формирование локального мира.
Правило 1. Локальный мир образуют случайно выбранная вершина i и ее 1-й, 2-й, …, n-й соседи (то есть вершины, расстояние до которых от i-й вершины меньше либо равно n); n фиксированное и является параметром модели. Фактически n представляет собой радиус локального мира.
Правило 2. M узлов локального мира выбираются в сети случайным образом. Здесь M фиксированное и является параметром модели.
Анализ топологии и характера корреляций локально-мировых сетей
Основной топологической характеристикой графа G является распределение степеней p(k), где p(k) определяется как вероятность того, что случайно выбранная вершина имеет степень k, или, что эквивалентно, как доля вершин графа, имеющих степень k.
Характер корреляций степеней вершин сети удобно анализировать с помощью функции  , определяющей зависимость средней степени ближайших соседей вершины от ее степени k [4]. Средняя степень ближайших соседей вершины степени k определяется как
, определяющей зависимость средней степени ближайших соседей вершины от ее степени k [4]. Средняя степень ближайших соседей вершины степени k определяется как 
 . Здесь
. Здесь 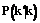 – вероятность того, что ребро, выходящее из вершины степени k, направлено к вершине степени
– вероятность того, что ребро, выходящее из вершины степени k, направлено к вершине степени 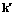 .
.  , где
, где  – число вершин степени k;
– число вершин степени k;  – симметричная матрица, элементы которой равны количеству ребер между вершинами степени k и
– симметричная матрица, элементы которой равны количеству ребер между вершинами степени k и 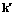 для
для 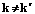 и удвоенному числу ребер, связывающих вершины одной и той же степени (
и удвоенному числу ребер, связывающих вершины одной и той же степени ( ). Если зависимость
). Если зависимость  – монотонно растущая функция, сеть является ассортативной (преимущественно соединены вершины, имеющие близкие степени); если
– монотонно растущая функция, сеть является ассортативной (преимущественно соединены вершины, имеющие близкие степени); если  – монотонно убывающая функция, сеть дисассортативна (вершины малой степени в основном связаны с вершинами большой степени и наоборот). Если
– монотонно убывающая функция, сеть дисассортативна (вершины малой степени в основном связаны с вершинами большой степени и наоборот). Если  не зависит от k, сеть некоррелированная.
не зависит от k, сеть некоррелированная.
В соответствии с описанными алгоритмами сгенерированы локально-мировые сети при различных способах формирования локального мира. Были построены распределения степеней, и для выявления наличия и характера корреляций в сети вычислены зависимости средней степени ближайших соседей вершины от ее степени  .
.
На рисунке 1 приведены графики распределений степеней вершин сгенерированных локально-мировых сетей, во всех трех случаях  и размер сети
и размер сети  . На рисунках 1а и 1b показано, соответственно, распределение степеней для сетей, сгенерированных по правилу 1 при n=1 (локальный мир сформирован случайно выбранной вершиной и ее первыми соседями) и при n=2 (вершина и ее первые и вторые соседи). На рисунке 1с представлено распределение степеней для сети со случайным выбором локального мира (правило 2) при M=3.
. На рисунках 1а и 1b показано, соответственно, распределение степеней для сетей, сгенерированных по правилу 1 при n=1 (локальный мир сформирован случайно выбранной вершиной и ее первыми соседями) и при n=2 (вершина и ее первые и вторые соседи). На рисунке 1с представлено распределение степеней для сети со случайным выбором локального мира (правило 2) при M=3.
Значения показателей степени g определялись с помощью метода максимального правдоподобия и равны 4.9 и 4.5 для распределений a, b соответственно. Как известно, значения g>3 характерны для сетей с суперхабами, то есть практически все вершины сети оказываются связанными с одной или несколькими вершинами, имеющими очень большую степень [1]. Такие сети имеют резко выраженный дисассортативный характер. Действительно, зависимости  для сгенерированных сетей, представленные на рисунках 2a и 2b, имеют убывающий характер, то есть дисассортативны.
для сгенерированных сетей, представленные на рисунках 2a и 2b, имеют убывающий характер, то есть дисассортативны.
 На рисунке 1с показано, что локально-мировая сеть при случайном выборе локального мира и при M=m=3 характеризуется экспоненциальным распределением степеней. Соответствующая этой сети зависимость
На рисунке 1с показано, что локально-мировая сеть при случайном выборе локального мира и при M=m=3 характеризуется экспоненциальным распределением степеней. Соответствующая этой сети зависимость  (рис. 2c) имеет растущий характер, следовательно, эта сеть является ассортативной.
(рис. 2c) имеет растущий характер, следовательно, эта сеть является ассортативной.
Анализ локально-мировых сетей, сгенерированных в соответствии с правилом 1, показал, что при увеличении радиуса локального мира n топология сети практически не меняется. В таких сетях всегда присутствуют суперхабы, и эти сети всегда дисассортативны.
 Более гибкую структуру имеют сети со случайным выбором локального мира. На рисунке 3 представлено распределение степеней для такой сети при M>>m. Размер сети N~104, m=m0=3, M=500. Сеть имеет масштабно-инвариантный характер, g=2.9. Соответствующая зависимость
Более гибкую структуру имеют сети со случайным выбором локального мира. На рисунке 3 представлено распределение степеней для такой сети при M>>m. Размер сети N~104, m=m0=3, M=500. Сеть имеет масштабно-инвариантный характер, g=2.9. Соответствующая зависимость  показывает, что сеть некоррелированная. Таким образом, с ростом M происходит фазовый переход с изменением топологии сети от экспоненциальной к масштабно-инвариантной. Одновременно это сопровождается изменением характера корреляций: сети трансформируются от ассортативных к некоррелированным.
показывает, что сеть некоррелированная. Таким образом, с ростом M происходит фазовый переход с изменением топологии сети от экспоненциальной к масштабно-инвариантной. Одновременно это сопровождается изменением характера корреляций: сети трансформируются от ассортативных к некоррелированным.
Исследование устойчивости локально-мировых сетей к случайным отказам и направленным атакам
Обсудим топологические аспекты устойчивости сложных сетей. Рассмотрим произвольный связанный граф с N вершинами. Предположим, что из графа удаляется доля вершин p. Необходимо выяснить, является ли полученный подграф связным, чтобы определить, как связность подграфа зависит от доли удаленных вершин p. Оказывается, для широкого класса сетей существует порог  , такой, что при
, такой, что при  подграф будет оставаться связным, тогда как при
подграф будет оставаться связным, тогда как при  происходит его расщепление.
происходит его расщепление.
Для анализа устойчивости принято рассматривать два типа воздействий на сети: случайные отказы узлов и направленные атаки на узлы. В первом случае в сети случайным образом удаляются часть вершин p. Во втором из сети удаляются вершины со степенью, большей некоторой заданной степени  . Далее строятся зависимости доли вершин сети, принадлежащих наибольшей связной компоненте, от доли удаленных вершин (при изменениях p и
. Далее строятся зависимости доли вершин сети, принадлежащих наибольшей связной компоненте, от доли удаленных вершин (при изменениях p и  соответственно). Определяется порог – значение доли удаленных вершин, при котором сеть рассыпается [5].
соответственно). Определяется порог – значение доли удаленных вершин, при котором сеть рассыпается [5].
На рисунке 4 приведены результаты исследования устойчивости сетей к направленным атакам для различных способов формирования локально-мировых сетей. Для сравнения на рисунке приведены также результаты анализа устойчивости к направленным атакам для аналогичной сети БА.
Видно, что наиболее устойчивыми к направленным атакам являются локально-мировые сети со случайным выбором локального мира при M=m=3, при этом пороговое значение pc=0.57. Наименее устойчивыми в этом случае будут локально-мировые сети, в которых локальный мир формируется по принципу соседства. Они имеют очень малые пороговые значения pc=0.02, pc=0.03 соответственно, являясь более неустойчивыми по отношению к направленным атакам. Это непосредственно связано с топологией данных сетей.
Результаты устойчивости рассматриваемых сетей к случайным отказам показывают, что сети, сгенерированные в соответствии с описанными правилами, ведут себя практически одинаково. Пороговое значение pc=0.9, что означает достаточно большую устойчивость этих сетей к такого рода воздействиям.
Подводя итог, можно отметить, что в статье рассмотрены различные механизмы формирования локально-мировых сетей, предложены соответствующие алгоритмы для их генерации, проведены исследования топологии, характера корреляций и устойчивости этих сетей к случайным отказам и направленным атакам.

 Кроме того, показано: если локальный мир формируется соседями случайно выбранного узла, это приводит к сети с суперхабами, которые дисассортативны и наименее устойчивы к направленным атакам. Сети со случайным выбором локального мира имеют более гибкую структуру. Если размер локального мира совпадает с числом ребер, поступающих в сеть на каждом временном шаге, сеть имеет экспоненциальную топологию. С увеличением размера локального мира происходит топологический фазовый переход, в результате которого топология сети становится масштабно-инвариантной. Сети с экспоненциальной топологией оказываются наиболее устойчивыми к направленным атакам.
Кроме того, показано: если локальный мир формируется соседями случайно выбранного узла, это приводит к сети с суперхабами, которые дисассортативны и наименее устойчивы к направленным атакам. Сети со случайным выбором локального мира имеют более гибкую структуру. Если размер локального мира совпадает с числом ребер, поступающих в сеть на каждом временном шаге, сеть имеет экспоненциальную топологию. С увеличением размера локального мира происходит топологический фазовый переход, в результате которого топология сети становится масштабно-инвариантной. Сети с экспоненциальной топологией оказываются наиболее устойчивыми к направленным атакам.
По отношению к случайным отказам все рассмотренные сети ведут себя практически одинаково устойчиво.
Таким образом, масштабно-инвариантные сети уязвимы к направленным атакам и достаточно устойчивы к случайным отказам.
Необходимо подчеркнуть, что важнейшими примерами локально-мировых сетей являются Интернет и WTW.
Литература
1. Albert R., Barabási A.-L. Statistical Mechanics of Complex Networks // Rev. Mod. Phys. 2002. Vol. 74, pp. 43–97.
2. Boccaletti S., Latora V., Morena Y., Chavez M. Complex networks: Structure and dynamics // Physics Reports. 2006. Vol. 424, pp. 175–308.
3. Li X., Jin Yu Ying, Chen G. Complexity and Synchronization of the World trade Web // Physica A. Vol. 328, pp. 287–296.
4. Pastor-Satorras R., Vespignani A. Evolution and Structure of the Internet: a statistical physics approach. – Cambridge University Press, 2004.
5. Гаджиев Б.Р., Прогулова Т.Б., Щетинина Д.П. Статическая устойчивость ассортативных и дисассортативных сетей / Математика. Компьютер. Образование: сб. научн. тр. Т. 2; под ред. Г.Ю. Ризниченко. М.–Ижевск: НИЦ «Регулярная и хаотическая динамика», 2007. С 22–29.



 , где
, где 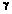 – показатель степени. В отличие от случайных и мало-мировых масштабно-инвариантные сети имеют сильно неоднородную структуру. Анализ топологии сетей реального мира показал, что многие из искусственных систем характеризуются степенным распределением.
– показатель степени. В отличие от случайных и мало-мировых масштабно-инвариантные сети имеют сильно неоднородную структуру. Анализ топологии сетей реального мира показал, что многие из искусственных систем характеризуются степенным распределением. ). Модель БА приводит к сети, распределение степеней которой подчиняется степенному закону
). Модель БА приводит к сети, распределение степеней которой подчиняется степенному закону  . Несмотря на то, что БА-модель объясняет основные особенности большей части сетей реального мира (степенной характер распределения степеней, динамику роста степеней отдельных узлов и т.д.), строго фиксированное значение показателя g=3 является существенным недостатком модели. Так, анализ сетей реального мира показал, что значение показателя степени
. Несмотря на то, что БА-модель объясняет основные особенности большей части сетей реального мира (степенной характер распределения степеней, динамику роста степеней отдельных узлов и т.д.), строго фиксированное значение показателя g=3 является существенным недостатком модели. Так, анализ сетей реального мира показал, что значение показателя степени  [1, 2]. Очевидно, что эта особенность связана с присутствием дополнительных механизмов роста сетей. Обобщенная модель предполагает следующие механизмы роста сети.
[1, 2]. Очевидно, что эта особенность связана с присутствием дополнительных механизмов роста сетей. Обобщенная модель предполагает следующие механизмы роста сети. .
. , определяющей зависимость средней степени ближайших соседей вершины от ее степени k [4]. Средняя степень ближайших соседей вершины степени k определяется как
, определяющей зависимость средней степени ближайших соседей вершины от ее степени k [4]. Средняя степень ближайших соседей вершины степени k определяется как 
 . Здесь
. Здесь 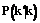 – вероятность того, что ребро, выходящее из вершины степени k, направлено к вершине степени
– вероятность того, что ребро, выходящее из вершины степени k, направлено к вершине степени 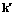 .
.  , где
, где  – число вершин степени k;
– число вершин степени k;  – симметричная матрица, элементы которой равны количеству ребер между вершинами степени k и
– симметричная матрица, элементы которой равны количеству ребер между вершинами степени k и 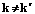 и удвоенному числу ребер, связывающих вершины одной и той же степени (
и удвоенному числу ребер, связывающих вершины одной и той же степени ( ). Если зависимость
). Если зависимость  и размер сети
и размер сети  . На рисунках 1а и 1b показано, соответственно, распределение степеней для сетей, сгенерированных по правилу 1 при n=1 (локальный мир сформирован случайно выбранной вершиной и ее первыми соседями) и при n=2 (вершина и ее первые и вторые соседи). На рисунке 1с представлено распределение степеней для сети со случайным выбором локального мира (правило 2) при M=3.
. На рисунках 1а и 1b показано, соответственно, распределение степеней для сетей, сгенерированных по правилу 1 при n=1 (локальный мир сформирован случайно выбранной вершиной и ее первыми соседями) и при n=2 (вершина и ее первые и вторые соседи). На рисунке 1с представлено распределение степеней для сети со случайным выбором локального мира (правило 2) при M=3.

 , такой, что при
, такой, что при  подграф будет оставаться связным, тогда как при
подграф будет оставаться связным, тогда как при  происходит его расщепление.
происходит его расщепление. . Далее строятся зависимости доли вершин сети, принадлежащих наибольшей связной компоненте, от доли удаленных вершин (при изменениях p и
. Далее строятся зависимости доли вершин сети, принадлежащих наибольшей связной компоненте, от доли удаленных вершин (при изменениях p и 

