Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Метод дообучения алгоритмов распознавания классов объектов
Аннотация:В статье представлен метод решения задачи корректировки статистического описания объектов распознавания в пространстве признаков. Использование данного метода позволяет повысить достоверность решений, принимаемых алгоритмами распознавания за счет учета дополнительной признаковой информации.
Abstract:The article presets a task solution method of statistical description correction of recognition subjects in space of criterions. Using this method allow to increase degree of certainty of maken decisions by recognitions algorithms at the expense of additional criterial information account.
| Авторы: Машкин А.В. (arep@cps.tver.ru) - 2 ЦНИИ Минобороны России, г. Тверь, кандидат технических наук, Бачев А.Г. (all_my_mail@mail.ru) - Военная академия воздушно-космической обороны им. Г.К. Жукова, г. Тверь, Малозёмов В.В. () - Военная академия воздушно-космической обороны им. Г.К. Жукова, г. Тверь | |
| Ключевые слова: пространство признаков, дообучение алгоритмов |
|
| Keywords: space of criterions, reinstruction method |
|
| Количество просмотров: 9180 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Формирование образов распознаваемых объектов осуществляется путем статистической обработки многократных наблюдений (измерений) значений признаков распознавания и формализации их в виде генеральной совокупности для каждого объекта [1]. При синтезе алгоритма распознавания генеральная совокупность значений фиксируется и, как правило, в дальнейшем не корректируется. Однако в процессе дальнейшего наблюдения за объектами любого класса появляется дополнительная признаковая информация, в том числе и принципиально отличающаяся от информации, полученной ранее. В связи с этим алгоритм распознавания должен обладать свойством адаптации к изменяющимся признаковым образам, то есть должен дообучаться. Под дообучением будем понимать процесс корректировки образного описания распознаваемых объектов на основе поступающей текущей признаковой информации и принятия решений о ее принадлежности. Цель работы заключается в разработке метода дообучения алгоритмов распознавания на основе анализа дополнительной признаковой информации. Если предположить, что априорные образы не являются абсолютно стабильными, то в процессе получения текущей измерительной признаковой информации, аппроксимируемой функцией плотности распределения для признака x – fтек(x), и отнесения ее с соответствующими вероятностями ко всем возможным M образам объектов из анализируемой совокупности необходимо корректировать априорные функции плотности каждого i-го образа – fi(x). Пусть априорный образ fi(x) был сформирован в результате NS испытаний. Площадь k-го столбца априорной гистограммы определяется из выражения:
где Nk – количество испытаний, попавших в k-й столбец априорной гистограммы; Получение текущего образа fтек(x) в процессе наблюдения за объектом физически означает наличие в признаковой области дополнительного испытания. При получении единичного текущего распределения fтек(x) площадь соответствующего столбца DSk выражается как
где DNk – числовая доля текущего испытания, попавшего в k-й столбец априорной гистограммы. Общее количество испытаний составляет NS+1. Следовательно, площадь столбца аддитивного распределения (совокупности априорного и текущего) представляется как
где Проведя преобразования с учетом (1–3), получаем выражение вида
трансформированный образ математически выражается как
Если было получено n текущих образов, то трансформация априорного образа примет вид
Однако такое представление справедливо при условии, что наблюдаемые текущие образы однозначно относятся к i-му объекту. В случае несоблюдения этого условия необходимо трансформировать априорные образы с учетом апостериорных вероятностей
Учитывая весовые коэффициенты в виде значений Pij (7), выражение (5) запишется как Расчеты показателей качества распознавания с использованием процедуры дообучения проводились для условий, когда объектами выступают радиоэлектронные средства – источники радиоизлучений. В качестве априорных образов рассматривались одномодальные функции плотности распределения вероятностей случайных значений частоты излучений радиоэлектронных средств. После реализации процедуры дообучения априорные образы трансформировались в полимодальные функции плотности, характеризующие законы распределения частот излучения в различных режимах работы радиоэлектронных средств. Для фиксированных условий проведения расчетов значения показателей качества изменялись в пределах единиц процентов. Таким образом, откорректированное статистическое описание объектов распознавания в пространстве признаков на основе поступающей дополнительной информации позволяет адаптировать алгоритмы. Это дает возможность более адекватно представлять объекты их статистическими образами, что, в свою очередь, приводит к повышению достоверности вырабатываемых решений. Литература 1. Левин Б.Р. Теоретические основы статистической радиотехники. В 3 кн. М.: Сов. радио, 1975. 2. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2378&page=article |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Назад, к списку статей



 (1)
(1)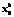 – координата центра k-го столбца априорной гистограммы; Dx – элемент вероятности, соответствующий ширине столбца гистограммы.
– координата центра k-го столбца априорной гистограммы; Dx – элемент вероятности, соответствующий ширине столбца гистограммы. , (2)
, (2) (3)
(3) – трансформированное априорное распределение, характеризующее образ i-го объекта.
– трансформированное априорное распределение, характеризующее образ i-го объекта. (4)
(4) (5)
(5) (6)
(6) , означающих вероятности отнесения j-го текущего образа к i-му априорному распределению. Расчет величин может производиться с использованием известной формулы Байеса [2]:
, означающих вероятности отнесения j-го текущего образа к i-му априорному распределению. Расчет величин может производиться с использованием известной формулы Байеса [2]: (7)
(7) а формула (6) в виде
а формула (6) в виде 
