Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Автоматизированная система рентгеноструктурного анализа поликристаллов
Аннотация:Cтатья посвящена разработке программной системы автоматизированного рентгеноструктурного анализа данных порошковой дифракции. В основе ее лежит новый гибридный двухуровневый генетический алгоритм глобальной оптимизации. Апробация системы показала, что существенно упрощается и автоматизируется процесс определения кристаллической структуры, обеспечивая высокую точность результатов.
Abstract:Development of the program system for automated X-Ray structure analysis from powder diffraction data is reported. The system is based on a new hybrid genetic algorithm of global optimization. As approval suggests, the system allows substantial facilitating and automating the process of crystal structure determination providing highly accurate results.
| Авторы: Семенкин Е.С. (styugin@rambler.ru) - Сибирский государственный аэрокосмический университет им. академика М.Ф. Решетнева, г. Красноярск, Россия, Якимов Я.И. (yar_yakimov@mail.ru) - Сибирский федеральный университет, г. Красноярск | |
| Ключевые слова: количественный фазовый анализ, порошковая дифракция, кристаллическая структура, рентгеновский структурный анализ, гибридный генетический алгоритм |
|
| Keywords: quantitative phase analysis, powder diffraction, crystal structure, X-ray structure analysis, hybrid genetic algorithm |
|
| Количество просмотров: 9504 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Определение атомной структурной модели неизвестного кристаллического вещества – наиболее трудная задача в исследованиях новых веществ и материалов, особенно, когда нет возможности получить достаточно большой кристалл вещества для исследования монокристальными методами. В этом весьма распространенном случае используют методы порошковой дифракции. Вследствие информационной бедности порошковой дифрактограммы – схлопывания трех пространственных измерений в одну размерность дифракционного профиля с перекрытием дифракционных пиков от большого числа разноориентированных кристаллитов – возникает проблема. Это накладывает фундаментальные ограничения на информацию, получаемую из профиля, и ее анализ. Дополнительные трудности создает частое наличие трудноотделимых примесей побочных фаз. Сравнительно новым и перспективным направлением решения проблемы поиска кристаллической структуры по данным порошковой дифракции является применение стохастических методов глобальной оптимизации в прямом пространстве, таких как Монте-Карло, имитация отжига, эволюционные алгоритмы [1]. Суть методов заключается в статистической генерации и критериальной эволюции тестовых структур с накоплением лучших из них для использования в последующих генерациях. Глобальный крите- рий качества при этом – соответствие профилей экспериментальной и тестовой модельной дифрактограмм, где вторая является сложной функцией большого числа параметров, описывающих форму профиля и непосредственно структурную модель. Формализуя задачу определения кристаллической структуры из данных порошковой дифракции, получаем следующую математическую задачу оптимизации. Экспериментальные данные (дифрактограмма) представляют собой дискретную последовательность {qj, Yj}. Имеется некоторый класс параметрических функций Y(P, Q), P – вектор профильных (центры, полуширина, форма, асимметрия линий и т.п.) и структурных параметров (координаты атомов, параметры их тепловых колебаний и др.), Q – независимый аргумент (дифракционный угол). Требуется найти функцию Yмод. из класса Y(P, Q) и оптимальный набор параметров Р* так, чтобы выполнялось условие:
Особенность задачи – большая размерность (может достигать 100 и более параметров) и неполиномиальность функций Y(P, Q). Как эффективное средство решения подобного рода многопараметрических оптимизационных задач в различных областях науки и техники зарекомендовали себя генетические алгоритмы (ГА) [2]. Они не требуют информации о свойствах целевой функции и, работая одновременно с целым рядом (популяцией) решений-индивидов, позволяют вести широкий поиск в пространстве решений, легко инкорпорируют экспертные знания, а также могут объединяться с процедурами локального поиска. Известны и работы по применению классического ГА для определения кристаллических структур [1]. Однако критическим фактором для методов глобальной оптимизации является их неустойчивая сходимость с блужданием в локальных экстремумах при увеличении размерности структурной задачи, определяемой сложностью (количеством степеней свободы) кристаллической структуры вещества. Кроме того, при решении практических задач возникает связанная с выбором функции Yмод. проблема «точность–размерность», напрямую влияющая на сходимость процесса поиска. Поэтому эффективное применение подобных подходов на практике затруднительно и требует высокой квалификации исследователя, что приводит к необходимости максимально упростить и автоматизировать процесс определения структуры.
Отличительной особенностью предложенного алгоритма также является использование в качестве средства подгонки расчетной и экспериментальной дифрактограмм вместо классического метода Ритвельда нового, недавно предложенного метода минимизации производной разности (МПР) профилей [1]. Этот метод не требует моделирования фона дифрактограммы, при этом улучшая экстракцию слабых дифракционных рефлексов, что уменьшает размерность задачи и усиливает сходимость. Описанный двухуровневый ГА лежит в основе разработанной авторами автоматизированной системы рентгеноструктурного анализа поликристаллов. Система включает управляющий модуль, программную реализацию метода МПР и модуль, реализующий двухуровневый ГА (см. рис.). Исходными данными для анализа служат цифровая рентгенограмма, данные об условиях съемки, а также химический состав и симметрия всех фаз исследуемого образца. Эти данные вместе с параметрами ГА задаются через гибкий графический интерфейс управляющего модуля. Система предоставляет широкий спектр возможностей, таких как визуальный контроль и динамическое управление процессом поиска ГА, многоуровневое накопление информации о ходе процесса поиска, визуализация и экспорт результатов, в том числе построение 3d-моделей полученных структур. В целях многостороннего исследования процесса поиска по двухуровневому ГА в системе реализован ряд специальных инструментов-индикаторов. В зависимости от назначения их можно разделить на две группы: инструменты наблюдения и контроля процесса решения реальной структурной задачи и исследовательские средства для тестирования и конфигурирования ГА на задачах с известным структурным решением. Такие инструменты дают возможность оценить разброс значений параметров индивидов ГА и степень их отклонения от эталонных значений (если таковые известны), тем самым детально информируя по существу процесса поиска и позволяя динамически им управлять. С помощью получаемой информации можно в итоге определить влияние различных установок ГА на его сходимость и выработать механизмы динамической подстройки двухуровневого ГА. Программная система апробирована на задачах определения структуры монофазных и многофазных веществ с известной кристаллической структурой. В частности, была решена задача определения структуры соединения Pd(NH3)2(NO2)2 размерности 43 (26 структурных + 17 профильных параметров) с точностью до 0,1Å даже для легких атомов водорода. Кроме того, система в автоматическом режиме позволила определить количественный состав трехфазного образца Al2O3+CaF2+ +ZnO (решалась задача размерности 32) с точностью до 0,65 % по массе, что является очень высоким показателем для бесстандартного анализа. Эти результаты свидетельствуют о том, что использование двух различных типов индивидов и генетических операторов 1-го и 2-го уровней ГА позволяет добиться эффективного решения поставленной задачи определения кристаллической структуры. Разработанная система существенно упрощает процесс структурного анализа, в высокой степени автоматизируя его и при этом обеспечивая достаточно высокую точность результатов. Литература 1. Dinnebier R.E., Billinge S.J.L. Powder Diffraction Theory and Practice / Cambridge: Royal Society of Chemistry, 2008. 2. Michalewicz Z. Genetic algorithms + Data Structures = Evolution Programs / New York: Springer-Verlag, 1996. 387 p. 3. Yakimov Y.I., Semenkin E.S., Yakimov I.S. Two-level genetic algorithm for a full-profile fitting of X-ray powder patterns // Z. Kristallogr. Suppl. 2009. Vol. 30, pp. 21–26. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2379&page=article |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Назад, к списку статей



 . (1)
. (1)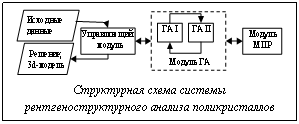 С учетом описанных проблем был разработан новый двухуровневый эволюционный алгоритм оптимизации. Его определяющая особенность и научная новизна заключаются в объединении двух принципиально разных ГА. Первый уровень предлагаемого алгоритма – классический гибридный ГА [2], работающий с двоичным представлением значений вектора искомых параметров P. Он предназначен для генерации тестовых структур и их ламарковской эволюции по критерию соответствия экспериментального и модельного профилей. В отличие от других подходов дополнительно используется 2-й уровень ГА, на котором лучшие тестовые структуры подвергаются локальной оптимизации с применением лучших в смысле сходимости вариантов уточнения совместных групп профильных и структурных параметров [3]. Второй уровень ГА работает с битовыми строками, каждая из которых задает для последующего уточнения локальным поиском подмножество параметров из P (то есть некоторое подпространство поиска) и в результате определяет порядок уточнения профильных и структурных параметров. Для выбора лучших вариантов уточнения используется эволюция битовых строк на основе специальных генетических операторов 2-го уровня, и лучшие уточненные структуры включаются в новую популяцию тестовых структур ГА 1-го уровня. Применение оптимизации тестовых структур на 2-м уровне понижает требования к точности кодирования параметров на 1-м уровне ГА и, соответственно, увеличивает число испытуемых вариантов структур, повышая эффективность ГА в целом. Это создает возможность автоматизированного решения структурной задачи. Дополнительно (в случае многофазного порошка) алгоритм может легко применяться и для решения задачи количественного фазового анализа.
С учетом описанных проблем был разработан новый двухуровневый эволюционный алгоритм оптимизации. Его определяющая особенность и научная новизна заключаются в объединении двух принципиально разных ГА. Первый уровень предлагаемого алгоритма – классический гибридный ГА [2], работающий с двоичным представлением значений вектора искомых параметров P. Он предназначен для генерации тестовых структур и их ламарковской эволюции по критерию соответствия экспериментального и модельного профилей. В отличие от других подходов дополнительно используется 2-й уровень ГА, на котором лучшие тестовые структуры подвергаются локальной оптимизации с применением лучших в смысле сходимости вариантов уточнения совместных групп профильных и структурных параметров [3]. Второй уровень ГА работает с битовыми строками, каждая из которых задает для последующего уточнения локальным поиском подмножество параметров из P (то есть некоторое подпространство поиска) и в результате определяет порядок уточнения профильных и структурных параметров. Для выбора лучших вариантов уточнения используется эволюция битовых строк на основе специальных генетических операторов 2-го уровня, и лучшие уточненные структуры включаются в новую популяцию тестовых структур ГА 1-го уровня. Применение оптимизации тестовых структур на 2-м уровне понижает требования к точности кодирования параметров на 1-м уровне ГА и, соответственно, увеличивает число испытуемых вариантов структур, повышая эффективность ГА в целом. Это создает возможность автоматизированного решения структурной задачи. Дополнительно (в случае многофазного порошка) алгоритм может легко применяться и для решения задачи количественного фазового анализа.