Программные продукты и системы

Стремительный прогресс в технологии создания узлов и блоков радиоэлектронной (РЭА) и электронно-вычислительной аппаратуры (ЭВА) обусловливает потребность в новых средствах автоматизированного проектирования. Количественный рост сложности объекта проектирования привел к качественным изменениям в методологии проектирования, к повышению роли математического обеспечения САПР. Это позволяет в области синтеза топологии выйти на следующий уровень программного обеспечения САПР. Исходными для проектирования являются спецификация прибора и технические требования к нему. Спецификация определяет логическую цель проектирования, технические требования – физические ограничения. Синтез топологий является одним из важнейших этапов в общей проблеме проектирования РЭА и ЭВА. В этой связи разработка алгоритмов проектирования топологии актуальна для новых поколений РЭА и ЭВА.

В работе рассмотрена одна из важнейших задач конструкторского проектирования РЭА и ЭВА – задача размещения. Она относится к классу NP (неопределенно распознаваемых за полиномиальное время) или является NP-полной, и для нее не известен алгоритм, растущий в полиномиальной степени. В этой связи разработка эффективных полиномиальных алгоритмов – актуальная и важная задача. В настоящее время появились генетические алгоритмы, ориентированные на решение задач размещения различного уровня иерархии [1–5]. Эти алгоритмы позволяют получать наборы квазиоптимальных решений, из которых конструктор может выбрать необходимые на основе заданного критерия качества. Переход к нанометровым нормам проектирования (100 нанометров и ниже) приводит к принципиальным трудностям технологического характера. Необходимо уменьшать площадь кристалла, паразитные емкости, улучшать быстродействие и снижать энергопотребление СБИС. Одним из подходов к решению этих задач является использование бионических методов. Они объединяют генетические, эволюционные, локального поиска и муравьиные алгоритмы. Это позволяет осуществлять параллельную разработку алгоритма размещения, а также коррекцию и изменение параметров процесса проектирования после каждого изменения технологических норм.

При решении задач конструкторского синтеза топологий для снижения размерности массивов информации выполняется декомпозиция задачи на более простые подзадачи [1–3]. Функциональные характеристики каждого компонента РЭА или ЭВА можно условно описать системой коммутационных, электрических, конструктивных и внешних параметров: F=F(A,B,C,D,Е,V).

Система A коммутационных параметров определяет число элементов и соединений компонентов. Система B электрических параметров в основном не зависит от коммутационных параметров. Здесь необходимо решать проблемы электрической совместимости, емкостного баланса и прочие. Система C конструктивных параметров определяет размеры компонентов, внутренних элементов, толщину, длину и изгиб соединений, система D – возможности дублирования и троирования элементов, а также минимизацию задержки сигналов и оптимизацию временных параметров. Система E определяется ЛПР, то есть конструктором, и представляет собой набор расплывчатых множеств и инструкций [2–4]. Система V выделена отдельно для учета технологий энергосбережения и потребления при проектировании.

Для большинства задач размещения применимы комбинированные алгоритмы случайного и направленного поиска. К ним можно отнести методы, инспирированные природными системами, моделирования отжига, методы силовой релаксации, групповых, парных перестановок и т.д. [4–5].

Комплексное решение задачи синтеза топологий при совместном разбиении, размещении соединений может вызвать ухудшение качественных показателей, особенно на этапах размещения и планирования кристаллов. В связи с этим задачу оптимального или квазиоптимального размещения компонентов предлагается разбивать на этапы или подэтапы, которые должны реализовываться параллельными, последовательными или комплексными методами. Эффективным методом уменьшения размерности задачи размещения является выбор нечетких подсистем топологических пара­метров. Это целесообразно для получения первоначального решения, которое может стать проб­разом будущих популяций альтернативных решений. Использование топологических параметров позволяет прежде всего анализировать взаимное расположение элементов в топологическом про­странстве. Конкретизацию размещения элементов, заключающуюся в определении их физических координат на поле кристалла, предлагается вы­полнять на заключительном этапе размещения [5].

Размещением компонентов на монтажно-коммутационном пространстве называется процесс распределения элементов в одном конструктивном уровне в соответствии с заданными критериями. Основным комплексным критерием является мера оценки электромагнитотепловой совместимости при размещении [1]. Данный критерий определяет область допустимых размещений элементов на плоскости, на которой могут быть заданы другие критерии – длина критических связей, число изгибов, толщина проводящих соединений, число конструктивно законченных блоков, длина задержки сигнала, величина энергопотребления, число соединений между конструктивными блоками, количество связей внутри блоков, функциональная полнота блоков. Распространенным критерием при размещении является суммарная длина внутренних соединений. Выполнение этого критерия обеспечивает минимизацию задержки сигнала, эффективную трассировку схемы, повышение надежности монтажа и т.д. В связи с этим анализ и исследование методов размещения компонентов и блоков ЭВА проводятся в основном на базе критерия суммарной длины соединений, суммарного числа изгибов проводников и суммарного числа пересечений связей суммарной величины энергопотребления.

Для эффективного решения задач размещения требуется разработка таких эвристических методов и алгоритмов, которые эффективно реализовывались на ЭВМ. В связи с этим используются абстрактные математические модели схем соединений монтажно-коммутацион­ного пространства. Часто задачи размещения решают путем разбиения исходной коммутационной схемы на уровни. Приемлемой моделью для размещения, как известно, являются графы различного вида [3–5]. Граф должен адекватно отражать конструктивные свойства схемы и нести в себе определенные знания о решаемых задачах.

Существует большое число методов построения графовых моделей коммутационных схем,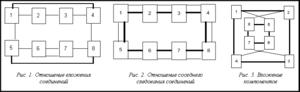

подлежащих размещению. Широко используемый метод заключается в том, что элементам схемы соответствуют вершины графа хiХ, а электрические цепи представляются ребрами ujU, X={x1,x2,…,xn }, |X|=n, U={u1,u2,…,um}, |U|=m. Заметим, что каждый узел в схеме соединений в общем случае должен представляться в графе G полными подграфами. При переходе от схемы соединений к графу за счет развязки узлов (узел соответствует соединению всех элементов между собой) в графе появляются лишние ребра, то есть соединения, фактически не существующие в коммутационной схеме. Это, с одной стороны, вносит избыточную информацию, а с другой – может позволить перестраивать структуру графа после каждого этапа алгоритма. Пошаговая перестройка дерева подграфа дает возможность изменять структуру при размещении элементов. Можно использовать указанный метод для перестройки структуры математической модели. Элементы этого множества являются нечеткими кортежами. Каждый кортеж задает ребро графа или упорядоченное соединение. Каждому соединению ставится в соответствие весовая функция, учитывающая частичное энергопотребление. Поиск эйлерова цикла на таком графе позволяет находить цепи с суммарным квазиоптимальным числом энергопотребления. На рисунке 1 показано такое отношение соединений, когда одно вкладывается в другое.

На основе информации о таком расположении контактов определим два типа бинарных отношений ψ= [2, 3]. В первом отношении ψ1= реализуется отношение соседнего следования (рис. 2).

Во втором отношении ψ2= реализуется отношение вложения соединений (рис. 1). Здесь F, F1, F2 – графики нечетких отношений; М – четкое множество, М={1,…,8}, определяющее область задания отношений. На этом множестве строится нечеткое множество, которое задает степень принадлежности соединений к элементам. Это выполняется на основе выбранных критериев. Можно описать любые возможные способы представления коммутационных моделей. При анализе соединений внутри блока используются вертикальные или горизонтальные разрезы, определенные пропускной способностью соответствующего компонента. При расположении компонентов внутри друг друга представляется модель, показанная на рисунке 3.

Для минимизации внутренних пересечений ребер предлагаются перестановка, поворот или другая коммутация контактов внутреннего блока.

Если при переходе от схемы соединений блоков ЭВА к математической модели конкретная структура (структура покрывающих деревьев) несущественна, то удобным отображением такой схемы является гиперграф или его представление. Говорят, что задан гиперграф Н=(X, E), если задано множество вершин X={x1,x2,…,xn}, |X|=n, E={e1, e2,…,em}, |E|=m, причем каждое ребро представляет собой некоторое подмножество множества вершин, то есть ejÍX, jÍJ, J={1,2,...,m} [3–5]. Для представления коммутационной схемы соединений гиперграфом каждому элементу i={1, 2,...,n} схемы ставится в соответствие вершина хiÎХ гиперграфа. Если электрическая цепь j соединяет элементы схемы s,t,…,w, то вершины хs,хt,....,хw образуют ребро ej={хs,хt,....,хw}. Отметим, что один элемент схемы может принадлежать различным электрическим цепям.

Использование предложенных моделей позволяет осуществлять свертывание и декомпозицию схем большой размерности. Это дает возможность выполнять синтез различных вариантов размещения путем построения иерархической многоуровневой декомпозиционной структуры модели. При нежестких ограничениях на количество связей данные модели позволяют в интерактивном режиме выбирать модели, ориентированные на знания о решаемых задачах.

Опишем структуру бионического алгоритма. Сначала определим критические связи в графовой или гиперграфовой модели анализируемой коммутационной схемы. Если выбран критерий критических связей, а рассматриваемая схема не содержит таковых, осуществляется переход к реализации критерия суммарной величины энергосбережения на основе бионического поиска. Если анализируемая схема содержит критические связи, то осуществляем их размещение в линейки и формируем популяцию альтернативных решений. Применяем генетические операторы. Далее определяем критерий останова бионического поиска. Если критерий останова не достигнут, переходим на следующую итерацию бионического поиска. В том случае, если все итерации исчерпаны, выводим полученное минимальное значение интегрированного критерия оценки качества размещения и строим соответствующее ему размещение.

Предложенная стратегия позволяет быстрее находить локально-оптимальные результаты. Это связано с параллельной обработкой множества альтернативных решений. Причем на основе такого подхода возможно концентрирование поиска на получение более перспективных решений. Отметим, что периодически в каждой итерации можно проводить различные изменения в перспективных, неперспективных и других решениях.

На основании изложенного можно сделать следующие выводы. Разработана программная среда для задач проектирования. При построении комплекса программ использовались пакеты Borland C++, Builder, Visual C++. Была протестирована серия из 500 графовых моделей на 500, 1000 и 5000 вершин. При этом временная сложность алгоритма не выходила из области полиномиальной сложности. В лучшем случае временная сложность алгоритма »O(nlogn), в худшем случае – O(n3), где n – число вершин графовой модели. Отметим, что отличительной особенностью разработанного алгоритма является способность хорошо работать на популяциях с малым числом альтернативных решений, что уменьшает время реализации алгоритма. Полученные результаты позволяют говорить об эффективности метода и целесообразности использования в решениях других задач оптимизации.

Литература

1.  Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 360 с.

2.  Курейчик В.В., Неупокоева Н.В. Решение оптимизационных задач на основе генетических алгоритмов // Перспективные информационные технологии. 2000. № 2. С. 113–116.

3.   Курейчик В.В., Курейчик В.М. Генетический алгоритм размещения графа // Изв. РАН. Теория и системы управления. 2000. № 5. С. 67–74.

4.   Курейчик В.М., Лебедев Б.К., Лебедев О.Б. Решение задачи размещения на основе эволюционного моделирования // Там же. 2007. № 4. С. 78–90.

5.   Гладков Л.А., Курейчик В.В., Курейчик В.М., Сороколетов П.В. Биоинспирированные методы в оптимизации. М.: Физматлит, 2009.