Программная реализация эволюционного алгоритма решения одной задачи автоматической классификации
| Керимов А.К. (adalat_kerim@mail.ru) - Азербайджанский государственный экономический университет, г. Баку, доктор физико-математических наук, Давудова Р.И. (d.rewana@rambler.ru) - Институт кибернетики Национальной академии наук Азербайджана, г. Баку | |
| Ключевые слова: ген, потомок, особь, популяция, мутация, кроссовер (кроссинговер), дарвинизм, ламаркизм, эволюция |
|
| Keywords: gene, child, person, population, mutation, crossover, Lamark's and Darwin's evolution, hypergraph, evolution |
|
|
|
|
В статье рассматривается задача построения оптимальной классификации без обучения объектов (автоматическая классификация), характеризующихся количественными признаками. Искомая (оптимальная) классификация представляет собой решение некоторой задачи минимизации определенного типа функционала, характеризующего качество классификации. Данная проблема решается в рамках трехпараметрической модели алгоритма вычисления оценок (АВО) [1, 2], а оптимизация соответствующего функционала, характеризующего качества классификации, проводится с применением эволюционного алгоритма по принципу Ж. Ламарка. Пусть дано множество допустимых однотипных сложных объектов:
состояния которых описываются набором некоторых числовых признаков
Здесь T - прямоугольная матрица; xij - j-й признак i-го объекта; Mj - ограниченная область изменения j-го признака. Множество объектов (1) считается допустимым, если признаки (2) определены областью значений Mj, то есть для "i xijÎMj, где Определение 1. Подмножества 1) 2) 3) для 4) для и Предполагается, что количество классов l до классификации неизвестно. Задача автоматической классификации состоит в том, чтобы по описанию допустимых объектов (2) вычислить значения предикатов
Для решения рассматриваемой задачи предложен подход, комбинирующий два алгоритма - входящий в семейство АВО [1, 2] и эволюционный алгоритм по принципу Ламарка [3]. Задача решается в два этапа. На первом этапе сформулированная задача решается в рамках (n+2)-параметрической модели АВО. В этой модели введен вектор пороговых параметров Введем вектор весов признаков Понятия близости определяются в соответствии с АВО (табл. 1). Таблица 1
На первом этапе для начального значения вектора На втором этапе для оптимизации полученной классификации осуществляется минимизация функционала, характеризующего качество классификации (3) с применением эволюционного алгоритма по принципу Ламарка, то есть
где
История эволюционных вычислений началась с разработки различных независимых моделей эволюционного процесса. В отличие от эволюции природы эволюционные алгоритмы только моделируют те процессы в популяции, которые являются существенными для развития. По Чарльзу Дарвину, биологические популяции развиваются из поколения в поколение, подчиняясь законам естественного отбора, и выживает наиболее приспособленный. Генетические алгоритмы основаны на тех же процессах, что происходят с биологическими организмами. Основной идеей Ламарка, в отличие от Дарвина, является то, что организмы изменяются под воздействием окружающей среды и условий жизнедеятельности, а не только на генетическом уровне [3]. По теории эволюции Ламарка, характерные особенности организма, приобретенные им в результате адаптации на протяжении жизни, передаются его потомкам. Определение 2. Классификация, полученная из решения задачи (3), (4) и удовлетворяющая условиям 1–4 определения 1, называется оптимальной. В общем случае функционал (3) является ступенчатым и не обладает свойствами унимодальности и дифференцируемости, что исключает возможность применения классических методов оптимизации. Использование указанных методов порождает определенные проблемы, связанные со сходимостью итерационных процессов. В работе [4] для решения задачи автоматической классификации предлагается новый алгоритмический подход, состоящий из двух эвристических алгоритмов - алгоритма, входящего в семейство АВО, и самоорганизующегося генетического алгоритма, который выбирает приоритетную схему многородительской репродукции и эффективного числа родителей. В данной работе для решения задачи (3), (4) предлагается новый подход, базирующийся на эволюционном принципе Ж. Ламарка. Кратко опишем модифицированный эволюционный алгоритм по принципу Ламарка. Шаг 0. Пусть k=0. Шаг 1. Генерируется случайная начальная популяция. Шаг 2. Вычисляется функция приспособленности. Шаг 3. Из популяции случайно выбираются k_m особей и d_i битов для многоточечной мутации. Шаг 4. Проводится многоточечная мутация. Полученные особи остаются в популяции (заменяя своих родителей). Шаг 5. Случайно выбирается первый член пары скрещивания, вторым членом будет самая близкая к нему особь. Перейти к шагу 7 (инбридинг). Шаг 6. Выбираются максимально далекие особи (аутбридинг). Шаг 7. Проводится операция двухточечного кроссинговера между двумя выбранными особями. Полученные потомки заменяют в популяции обоих родителей. Шаг 8. Вычисляется целевая функция. Шаг 9. Проверяются условия для завершения алгоритма. Если условия удовлетворяются, необходимо остановиться, иначе принять k=k+1 и перейти к шагу 3. Проведены многочисленные вычислительные эксперименты при разных значениях m и n. Приведем один из них. Рассматривается задача автоматической классификации m=20 объектов (точек в пространстве), которые описываются n=3 признаками (координатами) (табл. 2). Значение вектора весов V=(1,1,1). Критерий завершения работы алгоритма выбирается следующим образом: если после двух последовательных итераций удовлетворяется условие Таблица 2 Значения матрицы признаков Т
Для рассмотренных объектов построена оптимальная классификация при пороговых значениях (2.53*10-1,3.28*10-1, 2.42*10-1), для которой значение функционала составляет 66.33335, а количество классов l=3. Вычислительные эксперименты показали, что при некоторых значениях e, dk, ds получается тривиальная классификация, то есть либо все объекты входят в один класс, либо каждый объект образует отдельный класс. При значениях e, dk, ds =(9.335938*10-1, 2.187500*10-1, 8.867188*10-1) получается первый случай, а для векторов (6.445313*10-1, 3.437500*10-1, 6.132813*10-1), (3.320313*10-1, 2.617188*10-1,8.867188*10-1), (5.585938*10-1, 9.023438*10-1, 7.539063*10-1) – второй случай. Оценивание вычислительной сложности предложенного алгоритма Если решение задачи проводится с применением суперпозиций нескольких алгоритмов A1, A2,..., Ap , то есть A=A1ÄA2Ä... ÄAp, причем i-й алгоритм имеет вычислительную сложность R(Ai), тогда для вычислительной сложности алгоритма A справедливо следующее: R(A)=R(A1)+ +R(A2)+ …+R(Ap). Таблица 3 Классификация объектов при разных значениях e, dk, ds
Верхние границы вычислительных сложностей отдельных программных модулей составляют, соответственно, вычислительной сложности предложенного алгоритма получается:
Итак, доказана следующая теорема: алгоритм, состоящий из суперпозиций АВО и эволюционного алгоритма для решения задачи авто- матической классификации m объектов, описываемых n количественными признаками, имеет вычислительную сложность В заключение следует отметить, что авторами предложен новый алгоритм, состоящий из комбинаций двух алгоритмов - алгоритма, входящего в семейство АВО, и эволюционного алгоритма по принципу Ламарка. Разработан программный комплекс, реализующий этот алгоритм, проведены вычислительные эксперименты. Оценена вычислительная сложность алгоритма, установлено, что этот алгоритм входит в класс эффективных алгоритмов P. Литература 1. Журавлев Ю.И., Никифоров В.В. Алгоритмы распознавания, основанные на вычислении оценок // Кибернетика. 1971. № 3. С. 1–11. 2. Зенкин А.А., Зенкин А.И. Задача построения оптимальных классификаций // Сб. работ по мат. кибернетике ВЦ АН СССР. М., 1981. С. 20–33. 3. Емельянов В.В., Курейчик В.В., Курейчик В.М. Теория и практика эволюционного моделирования. М.: Физматлит, 2003. 432 с. 4. Керимов А.К., Давудова Р.И. Генетический алгоритм в задачах автоматической классификации / Сб. докл. Междунар. конф. по мягким вычислениям и измерениям (SCM’2006). СПб, 2006. Т. 1. С. 250–252. 5. Керимов А.К., Давудова Р.И. Эволюционный алгоритм для решения задачи автоматической классификации // Искусственный интеллект и принятие решений. 2009. № 4. С. 74–79. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
http://swsys.ru/index.php?id=2418&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

 , (1)
, (1) . (2)
. (2) . Однотипными считаются системы, описание состояний которых дано в одном и том же признаковом пространстве. Таблицу Т называют признаковой матрицей. Каждый объект xi из (1) можно определить отображением
. Однотипными считаются системы, описание состояний которых дано в одном и том же признаковом пространстве. Таблицу Т называют признаковой матрицей. Каждый объект xi из (1) можно определить отображением  , где
, где 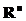 – пространство n-мерных векторов действительных чисел.
– пространство n-мерных векторов действительных чисел. , набора объектов X называются классами и удовлетворяют следующим условиям:
, набора объектов X называются классами и удовлетворяют следующим условиям: ;
; ;
;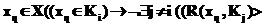
 , где
, где  – мера сходства объекта
– мера сходства объекта  и класса
и класса ;
;

 , где
, где  – мера сходства объектов xq и xt.
– мера сходства объектов xq и xt. , где
, где  , то есть
, то есть
 , где
, где  . Здесь
. Здесь  характеризует близость двух объектов по i-му признаку,
характеризует близость двух объектов по i-му признаку,  характеризует близость двух объектов,
характеризует близость двух объектов, 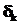 – близость объекта к классу. Вектор
– близость объекта к классу. Вектор  заменен обобщенным вектором
заменен обобщенным вектором  , где параметр
, где параметр  характеризует близость двух объектов по обобщенному признаку и связан с вектором
характеризует близость двух объектов по обобщенному признаку и связан с вектором  соотношениями
соотношениями 
 ,
, 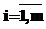 , то есть (n+2)-параметрическая модель сводится к трехпараметрической модели АВО [2].
, то есть (n+2)-параметрическая модель сводится к трехпараметрической модели АВО [2].
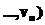 ,
,  ,
,  , компоненты которого задаются экспертно.
, компоненты которого задаются экспертно.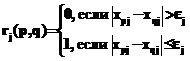




 вычисляются Г(p,q), по вычисленным значениям
вычисляются Г(p,q), по вычисленным значениям  строится начальная классификация и определяется начальное количество классов l. Для фиксированного
строится начальная классификация и определяется начальное количество классов l. Для фиксированного  , основываясь на R(p,Ki) и Г(p,Ki),
, основываясь на R(p,Ki) и Г(p,Ki),  , проводится уточнение полученной классификации.
, проводится уточнение полученной классификации. , (3)
, (3) – расстояние между объектами с номерами p и q; U - допустимая область трехмерного вектора пороговых оценок:
– расстояние между объектами с номерами p и q; U - допустимая область трехмерного вектора пороговых оценок: . (4)
. (4) то процесс заканчивается, в противном случае продолжается, где fk – значение функционала на k-й итерации; s – заданная точность. Результаты расчета приведены в таблице 3.
то процесс заканчивается, в противном случае продолжается, где fk – значение функционала на k-й итерации; s – заданная точность. Результаты расчета приведены в таблице 3. ,
,  ,
,  ,
, 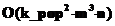 ,
,  ,
,  , где m – количество объектов; n – количество признаков; k_pop – количество особей, формирующих популяцию. Тогда для верхней границы
, где m – количество объектов; n – количество признаков; k_pop – количество особей, формирующих популяцию. Тогда для верхней границы
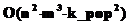 , иными словами, предложенный алгоритм принадлежит к классу эффективных алгоритмов P.
, иными словами, предложенный алгоритм принадлежит к классу эффективных алгоритмов P.