Решение задач глобальной оптимизации в среде распределенных вычислений
| Посыпкин М.А. (mposypkin@mail.ru) - Институт системного анализа РАН, Центр грид-технологий и распределенных вычислений, г. Москва | |
| Ключевые слова: распределенные вычисления, параллельные вычисления, конечномерная оптимизация |
|
| Keywords: distributed computing, parallel computing, global optimization |
|
|
|
|
Задачи глобальной оптимизации применяются в различных областях современной науки и техники. Они чрезвычайно важны для развития экономики в целом и таких отраслей, как нанотехнологии, микроэлектроника, биология, легкая и тяжелая промышленность. В этой связи разработка эффективных методов решения таких задач и их реализация в виде прикладных программных комплексов представляется актуальной научной и практической проблемой. Отличительной особенностью задач поиска глобального экстремума является высокая вычислительная сложность. Поэтому для решения таких задач целесообразно использовать методы параллельных и распределенных вычислений. В настоящее время наблюдается стремительное развитие архитектуры ЭВМ. Относительно недавно появились многоядерные процессоры, превратившие персональные компьютеры в параллельные системы с общей памятью. Быстро развивается сетевая инфраструктура, позволяющая выполнять вычисления в распределенной среде, состоящей из тысяч компьютеров, находящихся в географически удаленных точках. Многообразие архитектур и базового программного обеспечения (ПО) создает существенные трудности для программистов, которые вынуждены осваивать широкий спектр средств и методов разработки программ. Это приводит к потере эффективности труда исследователей и разработчиков ПО, обусловленной необходимостью изучать непрофильные области знаний. Предлагаемый в данной работе подход позволяет сэкономить усилия разработчиков за счет повторного использования общих для методов решения различных задач оптимизации частей. Фактически можно один раз реализовать общую схему решения для разных платформ, а в дальнейшем для конкретного класса задач использовать только проблемно-зависимые модули. После этого программа для решения конкретной задачи на заданной платформе получается объединением проблемно-зависимых модулей для этой задачи и проблемно-независимых модулей, реализующих общую схему для выбранной платформы. Задачи конечномерной оптимизации и методы их решения Задача поиска глобального минимума (максимума) функции f(x) на допустимом множестве XÍRn состоит в отыскании такой точки x*ÎX, что f(x*)£f(x)(f(x*)³f(x)) для всех xÎX. Предположим, что решается задача минимизации функции f. Ограничения, связанные с вычислительной погрешностью или недостатком ресурсов, часто не позволяют найти точное решение данной задачи. В этом случае следует перейти к поиску приближенного решения, то есть точки из множества e-оптимальных решений Способ задания множества X позволяет провести грубую классификацию задач. Если X=Rn, то задача относится к классу задач безусловной оптимизации. Если допустимое множество задано с помощью ограничений, то говорят об условной оптимизации. При этом, если X конечно, рассматриваемая задача относится к области дискретной оптимизации. Можно выделить два основных семейства методов решения задач конечномерной оптимизации – точные и эвристические. Точные методы позволяют гарантировать оптимальность найденного решения. К этому классу можно отнести различные варианты метода ветвей и границ, отсечений и др. Для точных методов характерна высокая трудоемкость, которая часто не позволяет применять их при решении реальных задач. Эвристические методы основаны на предположениях о свойствах оптимального решения. В отличие от точных эвристические методы не гарантируют оптимальность найденного решения. Однако в условиях ограниченности вычислительных ресурсов эвристики зачастую являются единственным способом нахождения решения. Распространены и гибридные методы, при которых эвристические методы применяются для нахождения решения, а точные – для доказательства оптимальности. Эффективность гибридных методов обусловлена тем, что эвристические алгоритмы нередко имеют более высокую скорость сходимости к оптимуму по сравнению с точными методами. Одной из наиболее распространенных схем организации точных методов является так называемый метод ветвей и границ (МВГ), основанный на разбиении допустимого множества. Приведем общую схему метода. На протяжении всего времени работы поддерживается список {Xi} подмножеств допустимого множества. Первоначально он состоит из одного элемента – допустимого множества X. Далее выбирается один из элементов списка – подмножество Xi. Если Xi удовлетворяет правилам отсева, выбранный элемент удаляется из списка. В противном случае он подвергается дроблению на более мелкие подмножества с помощью правила декомпозиции. Полученные подмножества замещают в списке выбранный элемент. Алгоритм завершает свою работу, когда в последовательности {Xi} не остается ни одного элемента. Правилом отсева будем называть любую функцию x:S®{0,1}, определенную на некотором множестве S подмножеств Rn и сопоставляющую каждому подмножеству из S число 0 либо 1. Если для некоторого VÎS выполняется x(V)=1, то будем говорить, что подмножество V удовлетворяет правилу отсева x. В противном случае будем утверждать, что V не удовлетворяет правилу отсева x. Пусть заданы правила отсева X={x1,..,xm}. Конечную совокупность подмножеств C={X1,..,Xt}, такую, что Приведем формулировку одного из наиболее часто применяемых правил отсева. Для этого понадобятся понятия оценки и рекорда. Оценкой называется функция g:S®R, определенная на множестве S подмножеств Rn, такая, что для любого VÎS выполняется
Совокупность правил отсева должна выбираться таким образом, чтобы из существования покрытия следовало, что найденный рекорд является e-оптимальным решением. В процессе нахождения рекорда последовательность точек x1,..,xk, в которых вычисляется значение целевой функции, формируется на основе разбиваемых множеств. Например, если множества {Xi} являются параллелепипедами, то в качестве элементов последовательности x1,..,xk берутся их центры. Также возможен подход, при котором последовательность точек x1,..,xk формируется независимым от построения покрытия способом с помощью различных эвристических процедур. В качестве эвристик могут применяться различные локальные алгоритмы (метод градиентного спуска, Ньютона, перебор в некоторой окрестности и т.п.), а также более сложные алгоритмы, например, стохастические или генетические подходы. Важная составляющая метода – правило декомпозиции D:S®2S, которое является функцией, определенной на множестве S подмножеств Rn и сопоставляющей некоторому подмножеству VÎS конечную совокупность его подмножеств V1,..,Vm, при этом Основные типы архитектур современных вычислительных систем Последовательные архитектуры. Классическая последовательная архитектура, предполагающая один поток команд и данных, в настоящее время не встречается даже на персональных компьютерах. Современные микропроцессоры, как правило, имеют несколько вычислительных ядер. При этом каждое ядро можно рассматривать как вычислитель с последовательной архитектурой. При планировании процессов и потоков операционная система рассматривает вычислительные ядра как независимые процессоры, не делая принципиальных различий между многоядерными и классическими архитектурами с общей памятью. Поэтому, несмотря на то, что в чистом виде последовательные архитектуры микропроцессоров практически не встречаются, существенная доля приложений использует именно модель последовательного выполнения. При этом основным средством разработки программ для решения вычислительных задач являются традиционные языки программирования С, С++, FORTRAN. Многопроцессорные системы с общей памятью. В системах с общей памятью предполагается наличие нескольких вычислительных ядер, которые имеют доступ к единому пространству памяти. Обмен данными между процессорами производится следующим образом: один процессор записывает данные по некоторому адресу, а другой считывает их. К этому классу относятся многопроцессорные рабочие станции и серверы, суперкомпьютеры с общей памятью (например HP Superdome), а также получившие широкое распространение многоядерные процессоры. При доступе к общей памяти необходима синхронизация для обеспечения эксклюзивного доступа к данным, которая реализуется с помощью таких механизмов, как мьютексы, семафоры, условные переменные. Основным инструментарием разработчика программ для архитектур этого типа являются библиотека для организации многопоточных вычислений POSIX Threads и пакет OpenMP. Многопроцессорные системы с распределенной памятью. Системы с общей памятью удобны с точки зрения разработки параллельных программ, они обеспечивают высокую производительность, но при большом числе процессоров очень дороги. Менее затратной альтернативой являются системы с распределенной памятью. В них каждый процессор имеет доступ только к своей локальной памяти, а между собой процессоры взаимодействуют с помощью передачи сообщений по сети. К этому классу относятся высокопроизводительные вычислительные кластеры, а также локальные сети. Нередки также ЭВМ с гибридной архитектурой, в которой узлы с общей памятью соединяются посредством сетевого оборудования. Основной парадигмой программирования для систем с распределенной памятью является передача сообщений. Наиболее распространенным средством разработки приложений в таких системах является MPI (Message Passing Interface). Библиотека MPI предоставляет набор функций для передачи сообщений между процессорами. Распределенные системы. Для выполнения вычислений могут использоваться не только специализированные многопроцессорные вычислительные комплексы, описанные выше, но и любая совокупность вычислительных ресурсов, объединенных сетью. При этом ресурсы могут располагаться в разных точках, иметь различную ведомственную принадлежностью и архитектуру. Для доступа к таким ресурсам применяются всевозможные механизмы. Некоторые узлы доступны через сетевой протокол прикладного уровня SSH. Ряд ресурсов может предоставляться с помощью различных программных средств промежуточного программного обеспечения грид (gLite, UNICORE, Globus) в рамках грид-ассоциаций. Рассмотрим распределенные вычислительные системы, состоящие из разнородных разноуровневых географически распределенных вычислительных ресурсов с различными способами доступа. Перечислим основные особенности распределенных систем, отличающие их от параллельных систем с распределенной памятью: · неоднородный состав: вычислительные узлы могут существенно отличаться по архитектуре, производительности, набору установленного ПО; · многообразие способов доступа к вычислительным узлам: для доступа могут применяться различные способы аутентификации и авторизации (secure shell, сертификаты X.509 и прочие способы доступа); · возможность изменения состава распределенной системы по ходу вычислений; · относительно невысокая и неоднородная скорость передачи данных между узлами. Между некоторыми узлами распределенной системы возможно установление прямого соединения, в других случаях необходимо применять механизмы туннелирования или обмен через файлы. Перечисленные различия между параллельными и распределенными системами обусловливают различия в подходах к численному решению задач на них. При организации распределенных вычислений необходимо применять методы динамической балансировки нагрузки, предусматривать возможность изменения состава распределенной среды в процессе вычислений и уметь синтезировать это пространство. Кроме этого, алгоритмы, предназначенные для использования в среде распределенных вычислений, должны допускать декомпозицию на совокупность слабо связанных друг с другом заданий, между которыми не происходит интенсивный обмен данными. Принципы реализации алгоритмов оптимизации на различных программно-аппаратных платформах Как известно, в настоящее время существует достаточно большое разнообразие платформ, от однопроцессорных до распределенных систем, содержащих десятки тысяч процессоров. Разработка ПО для решения задач оптимизации для каждой из этих платформ – достаточно сложная задача. Если требуется решать m задач оптимизации на n типах вычислительных устройств, то в общем случае нужно создать m´n различных программ. Предлагаемый в данной работе подход позволяет сэкономить усилия разработчиков за счет повторного использования общих частей, имеющихся у методов решения различных задач. Фактически можно один раз реализовать общую схему решения для разных платформ, а в дальнейшем для конкретного класса задач оптимизации реализовывать только проблемно-зависимые модули. После этого программа для решения определенной задачи на заданной платформе получается объединением проблемно-зависимых модулей для этой задачи и проблемно-независимых модулей, реализующих общую схему для выбранной платформы. В результате вместо m´n требуется разработать m+n программных модулей. Рассмотрим принципы реализации алгоритмов решения задач оптимизации для различных платформ. Последовательная реализация. Реализация для последовательной (однопроцессорной) архитектуры имеет важное самостоятельное значение и может рассматриваться в качестве базового блока реализаций для многопроцессорных архитектур. Метод ветвей и границ реализуется в соответствии с общей схемой. 1. Выбрать из списка {Xi} элемент Xi. 2. Выбрать точку xÎXÇXi и обновить рекорд fk+1=min(fk, f(x)). 3. Последовательно проверить выполнение правил отсева x1,..,xm. Если хотя бы для одного из правил имеет место xj(Xi)=1, то выполняется переход к шагу 1. Тем самым элемент Xi исключается из дальнейшего рассмотрения. 4. Произвести декомпозицию множества Xi и получить семейство подмножеств D(Xi)= Производительность данного алгоритма во многом определяется способом хранения списка подмножеств {Xi}. Наиболее легко реализуемой является организация хранения на базе очереди, стека или другого стандартного контейнера, предполагающего хранение полных копий создаваемых подмножеств. Недостатком такого способа хранения являются существенный объем памяти, требуемый для хранения подмножеств, и дополнительные расходы на копирование при добавлении элементов в список. Более экономным альтернативным вариантом является организация хранения информации на базе дерева ветвления. В ряде случаев целесообразно применение структур данных, ориентированных на конкретную задачу. Например, МВГ для задачи о ранце с одним ограничением может быть очень эффективно реализован на базе булева вектора [1]. Реализация для многопроцессорных архитектур с общей памятью. Рассмотрим традиционный многопоточный подход: параллельно выполняется несколько независимых потоков инструкций, имеющих доступ к общей памяти. Наиболее простым вариантом реализации представляется подход, при котором потоки независимым образом выполняют операции 1–4 последовательного алгоритма, описанного выше. При этом список {Xi} является общим для разных потоков. Для предотвращения ошибок при доступе к списку необходима синхронизация, обеспечивающая эксклюзивный доступ потоков к списку. Такая схема будет эффективно работать только при условии t1/N>>t2, где N – количество потоков; t1 – суммарное время выполнения локальных операций 2–3; t2 – суммарное время выполнения операций, требующих синхронизации, и самой синхронизации. Опыт реализации показывает, что для многих задач, например, для задачи о ранце, это соотношение не выполнено даже при небольшом (2–4) числе потоков. Более гибкая схема предполагает наличие локального списка у каждого из потоков дополнительно к общему списку. Обозначим список j-го потока через Lj. Поток j работает по следующей схеме. 1. Если Lj¹Æ, то выбрать XiÎLj. В противном случае (Lj=Æ) действия следующие: a) получить эксклюзивный доступ к общему списку {Xi}; b) если {Xi}¹Æ, то выбрать из списка {Xi} элемент Xi; иначе встать в ожидание до момента появления в списке хотя бы одного элемента {Xi}; c) закончить эксклюзивный доступ к спис- ку {Xi}. 2. Выбрать точку xÎXÇXi и обновить рекорд fk+1=min(fk, f(x)). 3. 4. Произвести декомпозицию множества Xi и получить семейство подмножеств D(Xi)= 5. Если число итераций кратно T, добавить S элементов из списка Lj в список {Xi}. Параметры T и S выбираются таким образом, чтобы обеспечивать заполнение списка {Xi}, не слишком часто прибегая к синхронизации. Для задач с высокой вычислительной сложностью возможно переполнение общего списка {Xi} за счет слишком интенсивного поступления подмножеств от потоков. Для предотвращения подобной ситуации вводятся два пороговых значения – m0 и M0, 0£m0£M0. Если число подмножеств в общем списке превосходит M0, процесс передачи подмножеств от потоков в общий список блокируется. В последующем, если количество подмножеств становится меньше m0, процесс передачи подмножеств возобновляется. Реализация для многопроцессорных архитектур с распределенной памятью. Общая идея реализации заключается в том, что каждый процессор работает со своим списком подмножеств, сохраняемым в локальной памяти. Если в результате выполнения разбиений локальный список становится пустым, для предотвращения простоев дополнительные множества пересылаются с другого процессора. Задача считается решенной, когда на всех процессорах списки не содержат подмножеств. В данной работе рассматриваются централизованные схемы организации вычислений: выделенный управляющий процессор отправляет рабочим процессорам области поиска и последний рекорд. Эти процессоры выполняют разбиение полученного подмножества, при необходимости пересылая на управляющий процессор часть подмножеств. Рассмотрим два возможных способа параллельной реализации нахождения рекорда в методе ветвей и границ. При первом подходе разбиение и нахождение рекорда выполняются на каждом процессоре, который периодически переключается между этими действиями. Такой способ особенно удобен, когда для построения рекорда используются точки, полученные в процессе разбиения, к которым применяется один из методов локальной оптимизации. В то же время в рамках данной схемы сложно создать параллельную реализацию алгоритма, работающего со всей совокупностью точек x1,..,xk. В этом случае предпочтительнее схема, при которой одна группа процессоров выполняет разбиение, а другая задействована в поиске рекорда (см. рис.). Рассмотрим базовую схему, подходящую для большинства алгоритмов, применяемых при нахождении рекорда. Выделенный управляющий процессор поддерживает список точек x1,..,xk. Некоторая точка удаляется из списка и рассылается всем либо определенным рабочим процессорам, которые подвергают ее процедуре оптимизации (как правило, одному из вариантов локального поиска). В результате на рабочем процессоре образуется список точек, который пересылается управляющему процессору и объединяется с его списком. Максимальная длина списка точек, правила выбора очередной точки для обработки, распределение точек по рабочим процессорам, способ добавления точек, полученных от рабочих процессоров к общему списку, локальный алгоритм являются параметрами общей схемы и определяют конкретный эвристический метод поиска рекорда. Список точек на управляющем процессоре может пополняться точками, полученными в результате разбиений. На рисунке процессы помечены следующим образом: M – процесс, управляющий работой всего приложения; {Bi} – процессы, которые выполняют операции разбиения; BM – процесс, координирующий работу процессов {Bi}; {Hi} – процессы, которые выполняют эвристический поиск; HM – координатор работы этих процессов. На начальном этапе процесс M рассылает исходные данные задачи остальным процессам. Разбиение выполняется группой, состоящей из управляющего процесса BM и рабочих процессов Bi. Процесс HM получает точки от процессов Hi и Bi, обновляет значение рекорда и рассылает его по всем процессам Bi, реализующим разбиения. Кроме того, HM направляет полученную точку всем (или некоторым, в зависимости от выбранного алгоритма) процессам Hi, выполняющим эвристический поиск. Если на процессе Hi удается улучшить рекорд, то соответствующая рекордная точка посылается процессу HM. Рассмотрим простой и достаточно эффективный алгоритм балансировки, построенный на тех же принципах, что и алгоритм управления потоками в случае общей памяти. Процесс Bi управляется двумя параметрами – T и S, посылаемыми ему управляющим процессом. Получив подмножество для обработки, Bi выполняет T разбиений, после чего пересылает S сгенерированных подмножеств на управляющий процесс BM. По окончании разбиения своего подмножества процесс Bi получает от BM новое подмножество. Для предотвращения переполнения памяти на управляющем процессе были введены два пороговых параметра – m0 и M0, 0£m0£ M0. Если число подмножеств на управляющем процессе становится больше M0, то управляющий процесс рассылает всем рабочим процессам новое значение T, равное -1, и процессы Bi перестают пересылать подмножества управляющему процессу BM. Когда число подмножеств на управляющем процессе становится меньше m0, он рассылает рабочим процессам первоначальные значения T, S, и передача подмножеств с рабочих процессов управляющему возобновляется. Реализация в среде распределенных вычислений. В отличие от параллельных распределенные системы имеют иерархическую организацию: они состоят из разнородных узлов, каждый из которых может, в свою очередь, быть параллельной системой, то есть одной из систем, рассмотренных в предыдущих разделах. Естественно предположить, что максимальная эффективность достигается, когда вычислительный процесс организован в соответствии с этой иерархией. При таком подходе на каждом из узлов вычисления выполняются по наиболее подходящей для данного узла схеме. Фактически на каждом из узлов распределенной системы выполняется отдельное приложение – солвер, выполняющее операции выбранного алгоритма оптимизации. Взаимодействие между несколькими приложениями организуется на следующем уровне иерархии через выделенный центральный управляющий процесс – супервизор. Первый этап решения задачи в распределенной вычислительной среде – синтез вычислительного пространства, которое формируется экземплярами солверов. При большом числе узлов запуск приложений вручную может быть достаточно трудоемким. Поэтому необходимо обеспечить возможность автоматизации запуска солверов супервизором. При этом используются средства удаленного запуска заданий, предусмотренные конкретной системой: SSH, грид-сервисы и др. Созданное вычислительное пространство может использоваться для решения задачи. В процессе решения необходимо распределять вычисления между солверами с целью обеспечения максимальной эффективности выполнения приложения в распределенной среде. Обмен данными между солверами и супервизором осуществляется средствами, предусмотренными для взаимодействия с конкретным узлом. Если имеется возможность установить прямое сетевое соединение, используются способы обмена, основанные на протоколах TCP/IP, например интерфейс сокетов. В некоторых случаях обмен данными с приложениями возможен только через передачу файлов средствами промежуточного ПО грид. Балансировка нагрузки происходит на двух уровнях: на верхнем уровне супервизор распределяет вычислительную нагрузку между солверами, а на нижнем (в пределах одного вычислительного узла) солвер распределяет работу методами, предназначенными для конкретного типа вычислительного узла. Практическая реализация Предложенный подход положен в основу реализации программных комплексов BNB-Solver [2] и BNB-Grid [3]. Программный комплекс BNB-Solver предназначен для решения задач оптимизации на многопроцессорных системах с общей и распределенной памятью. С его помощью были реализованы программы для решения задач о ранце, коммивояжере, непрерывной оптимизации. Результаты экспериментов показывают хорошие характеристики производительности по сравнению с аналогичными программными продуктами зарубежных исследователей [4]. Система BNB-Grid позволяет решать задачи оптимизации в среде, объединяющей несколько вычислительных кластеров. На каждом вычислительном кластере автоматически запускается один или более экземпляров BNB-Solver. Далее управляющий модуль BNB-Grid организует взаимодействие с запущенными приложениями. Вследствие наличия систем пакетной обработки на кластерах вычислительное пространство динамически изменяется в процессе расчетов. Поэтому в системе предусмотрены модули адаптивной иерархической балансировки нагрузки и резервного копирования на случай аварийного или принудительного завершения какого-либо из приложений. Программный комплекс BNB-Grid был применен для решения задачи поиска энергетически минимальной конформации однородного атомного кластера. В результате расчетов с помощью метода basin-hopping были найдены конфигурации, которые ранее не удавалось обнаружить с помощью данного метода [5]. Литература 1. Kellerer H., Pferschy U., Pisinger D. Knapsack Problems // Springer, Berlin, 2004. 2. Посыпкин М.А. Архитектура и программная организация библиотеки для решения задач дискретной оптимизации методом ветвей и границ на многопроцессорных вычислительных комплексах: тр. ИСА РАН. 2006. Т. 25. С. 18–25. 3. Афанасьев А.П., Посыпкин М.А., Сигал И.Х. Проект BNB-Grid: решение задач глобальной оптимизации в распре- деленной среде: тр. Второй междунар. конф. // Системный анализ и информационные технологии (САИТ-2007). 2007. Т. 2. С. 177–181. 4. Evtushenko Y., Posypkin M., Sigal I. A framework for parallel large-scale global optimization // Computer Science – Research and Development. 2009. № 23 (3), pp. 211–215. 5. Посыпкин М.А. Методы и распределенная программная инфраструктура для численного решения задачи поиска молекулярных кластеров с минимальной энергией // Параллельные вычислительные технологии (ПаВТ’2009): тр. Междунар. науч. конф. (Н. Новгород, 30 марта – 3 апреля 2009 г.). Челябинск: Изд-во ЮУрГУ, 2009. С. 269–281. |
http://swsys.ru/index.php?id=2420&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Облачный сервис «Параллельный Matlab»
- Исследование эффективности библиотеки MaLLBa на примере задач максимальной выполнимости
- Использование библиотеки MPI для параллельной реализации алгоритма полного перебора вариантов
- Разработка и применение распределенных пакетов прикладных программ
- Распределенная платформа для параллельного обучения искусственных нейронных сетей DisANN

 . Поиск точного решения можно рассматривать как частный случай поиска приближенного решения с e=0.
. Поиск точного решения можно рассматривать как частный случай поиска приближенного решения с e=0.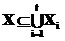 и для любого j={1,…,t} найдется хотя бы одно i={1,…,m}, такое, что xi(Xj)=1, будем называть покрытием множества X для набора правил отсева X.
и для любого j={1,…,t} найдется хотя бы одно i={1,…,m}, такое, что xi(Xj)=1, будем называть покрытием множества X для набора правил отсева X. . В качестве оценки, как правило, выбираются легко вычисляемые функции. Рекордом называют наименьшее значение целевой функции, найденное в процессе решения. Если x1,..,xk – последовательность точек, в которых вычислялось значение целевой функции, то
. В качестве оценки, как правило, выбираются легко вычисляемые функции. Рекордом называют наименьшее значение целевой функции, найденное в процессе решения. Если x1,..,xk – последовательность точек, в которых вычислялось значение целевой функции, то  – рекорд; xr – рекордное решение. Правило отсева xrec по рекорду формулируется следующим образом:
– рекорд; xr – рекордное решение. Правило отсева xrec по рекорду формулируется следующим образом:
 , ViÇVj=Æ для всех 1£i
, ViÇVj=Æ для всех 1£i
 . Добавить полученные подмножества к списку {Xi}.
. Добавить полученные подмножества к списку {Xi}.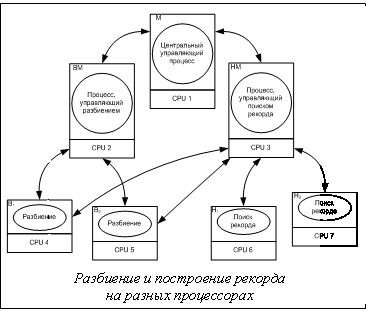 Последовательно проверить выполнение правил отсева x1,..,xm. Если хотя бы для одного из правил имеет место xj(Xi)=1, выполняется переход к шагу 1. Тем самым элемент Xi отбрасывается и становится элементом покрытия.
Последовательно проверить выполнение правил отсева x1,..,xm. Если хотя бы для одного из правил имеет место xj(Xi)=1, выполняется переход к шагу 1. Тем самым элемент Xi отбрасывается и становится элементом покрытия.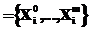 . Добавить полученные подмножества к списку Lj.
. Добавить полученные подмножества к списку Lj.