Совершенствование технологии процессов вывозки грузов путем моделирования и расчета элементов автодороги на криволинейных участках требует эффективной компьютерной поддержки. Существующие модели устройства переходных участков с кривыми переменного радиуса разрабатывались в расчете на применение эвристических методов расчета компенсации центробежной силы, действующей на движущееся по криволинейному участку автодороги транспортное средство. Устройство переходных кривых автомобильных дорог требует решения многочисленных задач для создания подсистемы соответствующего назначения в составе САПР автомобильных дорог, интегрированной с САПР технологической подготовки производства и организации вывозки грузов. Одной из таких задач является определение объема сектора составного виража, предложенного в качестве более эффективной модели криволинейного участка автомобильной дороги, с гладкой составной многоцентровой кривой (ГлСМК) в качестве трассы [1]. Использование составного виража для построения участков автодороги переменной и постоянной кривизны позволяет строить переходные участки, более точно вписанные в рельеф конкретной местности, что уменьшает общий объем работ по строительству автодороги.
В применяемой в настоящее время призматоидной модели [2] расчет профильного объема основных земляных работ производится по усредненным размерам призматоида на прямолинейном участке автодороги. Расчет объема земляных работ на криволинейных участках при использовании аналитических выражений для трассы криволинейного участка (клотоида, парабола) не рассматривается вообще и производится еще более приблизительно, с использованием нескольких поперечников.
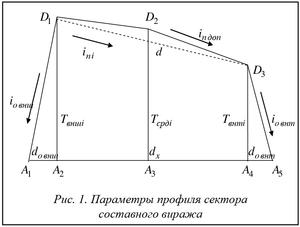
Предложена модель поперечного профиля кругового участка дороги, на базе которой созданы алгоритмы расчета параметров составного виража [3]. Результатом работы алгоритма является набор секторов составного виража. Каждый из этих секторов представляет собой многогранник, размеры которого можно определить исходя из параметров профиля (рис. 1) и плана (рис. 2) сектора составного виража.
 Профильный объем основных земляных работ при проектировании виража с помощью ГлСМК представляет собой сумму объемов всех секторов составного виража.
Профильный объем основных земляных работ при проектировании виража с помощью ГлСМК представляет собой сумму объемов всех секторов составного виража.
Полный объем всех секторов составит 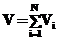 , где N – число секторов составного виража.
, где N – число секторов составного виража.
Из рисунка 3 видно, что объем Vi сектора i представляет собой сумму объемов четырех геометрических фигур: двух полуобелисков  ,
,  , полуклина
, полуклина  и фигуры
и фигуры  , которая, в свою очередь, состоит из половины параллелограмма
, которая, в свою очередь, состоит из половины параллелограмма  и двух фигур:
и двух фигур:  и
и  , объем каждой из которых представляет собой 1/8 часть объема пирамиды.
, объем каждой из которых представляет собой 1/8 часть объема пирамиды.
Таким образом, объем i-го сектора составного виража можно определить по формуле
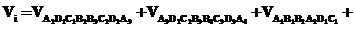
 , где i – номер сектора.
, где i – номер сектора.
Будем считать, что при определении объема i-го сектора составного виража известны:
- ширина d проезжей части (с учетом обочин и уширения);
- высоты Tвнтi и Tвншi внутреннего и внешнего краев проезжей части над нулевым уровнем;
- поперечный уклон проезжей части на рассчитываемом секторе ini;
- дополнительный поперечный уклон проезжей части inдоп;
- поперечные уклоны iовнт и iовнш внутреннего и внешнего откосов i-го сектора составного виража;
- центральный угол gi i-го сектора составного виража.
 Плоскость, содержащую точки A1, B1 и B5 (рис. 3), будем считать плоскостью нулевого уровня.
Плоскость, содержащую точки A1, B1 и B5 (рис. 3), будем считать плоскостью нулевого уровня.
Тогда объемы частей сектора i можно найти по формулам:
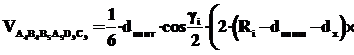
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Приведенные формулы достаточно громоздки для расчетов вручную. Поэтому применение ЭВМ для определения объема земляных работ при проектировании составного виража является оправданным с точки зрения трудозатрат.
Приведенная математическая модель предназначена для расчета объема сектора составного виража при построении криволинейного участка с использованием ГлСМК в качестве трассы [1]. По сравнению с существующей призматоидной моделью [2] обеспечивает более точный расчет профильного объема основных земляных работ, в результате чего стоимость общестроительных работ может быть снижена до 9 % по сравнению с прежними методами расчета, а нормативная трудоемкость при расчете – до 15 %.
Литература
1. Харин В.Н., Аникеев Е.А. Моделирование дорожных кривых с построением составного виража итерационным методом // Надежность и качество: тр. междунар. симпоз.; под ред. А.Н. Андреева. Пенза: Изд-во Пенз. гос. ун-та, 2000.
2. Алябьев В.И., Кувалдин Б.И., Грехов Г.Ф. Сухопутный транспорт леса: учебник для вузов. М.: Лесн. пром-сть, 1990.
3. Харин В.Н., Аникеев Е.А. Применение равнохордовых составных кривых в проектировании разворотов // Прикладные задачи моделирования и оптимизации: межвуз. сб. науч. тр.; под ред. проф. В.Н. Фролова. Воронеж: ВГТУ, 2000.





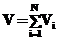 , где N – число секторов составного виража.
, где N – число секторов составного виража. ,
,  , полуклина
, полуклина  и фигуры
и фигуры  , которая, в свою очередь, состоит из половины параллелограмма
, которая, в свою очередь, состоит из половины параллелограмма  и двух фигур:
и двух фигур:  и
и  , объем каждой из которых представляет собой 1/8 часть объема пирамиды.
, объем каждой из которых представляет собой 1/8 часть объема пирамиды.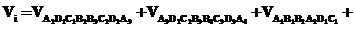
 , где i – номер сектора.
, где i – номер сектора.
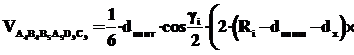
 ;
; ;
; ;
; ;
; .
.