Целью настоящей статьи являются построение нейросетевой модели для прогнозирования временных рядов финансовых данных на базе многослойного персептрона, обученного по алгоритму обратного распространения ошибки, а также формализация полной схемы применения данной модели для анализа и прогнозирования временных рядов на примере котировок акций российских эмитентов на ММВБ.
Актуальность исследования объясняется важностью получения качественных прогнозов основных финансовых индикаторов в условиях рыночной экономики, а также успешным опытом применения нейронных сетей в задачах прогнозирования.
В соответствии с целью работы решаются следующие задачи:
- обоснование применения моделей на основе нейронных сетей в задаче прогнозирования временных рядов;
- описание методики предварительной обработки временного ряда и формирования примеров для обучения нейронной сети;
- описание архитектуры и моделирование нейронной сети для прогнозирования временных рядов;
- описание и программная реализация алгоритма обучения нейронной сети на основе процедуры обратного распространения ошибки;
- построение прогноза будущих значений временного ряда.
Предлагаемая методика прогнозирования состоит из четырех основных этапов:
1) предварительный анализ временного ряда;
2) построение нейросетевой модели;
3) обучение нейронной сети по модифицированному алгоритму обратного распространения ошибки;
4) прогнозирование с помощью обученной нейросетевой модели.
Для решения задачи прогнозирования временного ряда zk, где k=0,1,…, находят применение нелинейные модели вида 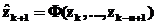 , где
, где  – некоторая нелинейная функция;
– некоторая нелинейная функция;  – прогнозируемое значение ряда;
– прогнозируемое значение ряда;  – наблюдаемые значения (предыстория ряда); n – порядок модели.
– наблюдаемые значения (предыстория ряда); n – порядок модели.
Эффективность нейросетевого подхода при прогнозировании временного ряда, основанного на данной модели, обосновывается теоремой об универсальной аппроксимации, которая утверждает, что многослойного персептрона с одним скрытым слоем достаточно для построения равномерной аппроксимации с точностью e для любого обучающего множества, представленного набором входов  и желаемых откликов
и желаемых откликов  . Тем не менее, из теоремы не следует, что один скрытый слой является оптимальным относительно времени обучения, простоты реализации, а также качества обобщения [1].
. Тем не менее, из теоремы не следует, что один скрытый слой является оптимальным относительно времени обучения, простоты реализации, а также качества обобщения [1].
Для моделирования динамики временного ряда в работе использована полносвязная нейронная сеть, в которой каждый нейрон слоя l связан со всеми нейронами предыдущего слоя l-1;  – синаптический вес, связывающий выход нейрона i со входом нейрона j на итерации n;
– синаптический вес, связывающий выход нейрона i со входом нейрона j на итерации n;  – функциональный сигнал, генерируемый на выходе нейрона i на итерации n. Пусть на нейрон j поступает поток сигналов от нейронов, расположенных в предыдущем слое, тогда индуцированное локальное поле
– функциональный сигнал, генерируемый на выходе нейрона i на итерации n. Пусть на нейрон j поступает поток сигналов от нейронов, расположенных в предыдущем слое, тогда индуцированное локальное поле  , полученное на входе функции активации, связанной с данным нейроном, вычисляется по формуле
, полученное на входе функции активации, связанной с данным нейроном, вычисляется по формуле
 , (1)
, (1)
где m – общее число входов (за исключением порога) нейрона j. Синаптический вес wj0 (соответствующий фиксированному входу y0=1) равен порогу bj, применяемому к нейрону j. Функциональный сигнал  на выходе нейрона j на итерации n равен
на выходе нейрона j на итерации n равен
 , (2)
, (2)
где jj – функция активации j-го нейрона. Функция активации – непрерывно дифференцируемая нелинейная функция. В качестве функции активации в работе используется функция гиперболического тангенса:
 , (a, b)>0, (3)
, (a, b)>0, (3)
где a и b – константы.
Нейронная сеть указанной структуры обучается по алгоритму обратного распространения ошибки в последовательном режиме, в котором корректировка весовых коэффициентов проводится после подачи каждого примера обучения вида  , где x(n) – входной вектор, поступающий на вход сети; d(n) – желаемый отклик; N – общее число примеров.
, где x(n) – входной вектор, поступающий на вход сети; d(n) – желаемый отклик; N – общее число примеров.
Изменение синаптических весов нейронов скрытых и выходного слоев сети, l=1,…,L, выполняется в соответствии с обобщенным дельта-правилом
 (4)
(4)
где  h – параметр скорости обучения; a – постоянная момента;
h – параметр скорости обучения; a – постоянная момента;  – сигнал ошибки выходного нейрона j на итерации n (соответствующий n-му примеру обучения) [1].
– сигнал ошибки выходного нейрона j на итерации n (соответствующий n-му примеру обучения) [1].
Цель обучения – минимизация суммарной среднеквадратической ошибки на всем обучающем множестве
 , (5)
, (5)
где d(n) – целевое значение для примера n;  – прогнозное значение.
– прогнозное значение.
Для извлечения прибыли от инвестиций на фондовом рынке важно получить точный прогноз направления тренда. Для повышения качества прогноза в целевой функционал I вводится штрафной коэффициент g, таким образом, целевой функционал будет вычисляться по формуле
 , (6)
, (6)
где  bÎ(0,1).
bÎ(0,1).
Для практической реализации алгоритма обратного распространения ошибки будем полагать, что сходимость алгоритма достигнута, если значение целевой функции I(w)0 – заранее заданный вещественный параметр, называемый точностью обучения [2].
Исходные данные для прогнозирования представляют собой табулированный текстовый файл, который содержит ежедневные котировки акций ОАО «Ростелеком» по цене закрытия. Файл содержит 248 записей, что соответствует временному интервалу в один календарный год [3].
Для улучшения качества прогноза исходный временной ряд подвергается предварительной обработке. На первом этапе предобработки данных использован метод сглаживания скользящим средним. Пусть zk, k=1,2,…N, – временной ряд длины N, тогда временной ряд  ,
,
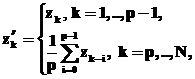 (7)
(7)
называется сглаженным временным рядом относительно zk, параметр p – период скольжения. Для сближения исходного и сглаженного рядов и сохранения тенденции исходного ряда в работе проведено сглаживание по трем членам временного ряда, то есть период сглаживания p=3 [4].
С целью получения качественного прогноза и сокращения времени обучения нейронной сети для анализа данных не следует выбирать сами котировки, которые обозначим zn (сглаженное значение котировки акции во время n=0,1,2,…). Действительно значимыми для предсказаний являются изменения котировок Dzn=zn–zn–1. Поэтому в качестве исходных данных логично выбирать наиболее статистически независимые величины, например, изменения котировок Dzn или логарифм относительного приращения 
 , ведущие себя более однородно, что особенно важно для длительных временных рядов, когда уже заметно влияние инфляции. Величины hn интерпретируются как «возврат», «отдача», «логарифмическая прибыль» [5].
, ведущие себя более однородно, что особенно важно для длительных временных рядов, когда уже заметно влияние инфляции. Величины hn интерпретируются как «возврат», «отдача», «логарифмическая прибыль» [5].
В данной работе в качестве исходных данных для прогнозирования используется логарифм относительного приращения сглаженных котировок.
Сформированный на этапе предварительной обработки набор исходных данных делится на два множества – обучающее и тестовое. Обучающие данные подаются сети для обучения, а тестовые – для расчета ошибки сети. Исследуемый в работе временной ряд состоит из 248 элементов, из которых первые 223 составляют обучающее множество, а последние 25 – тестовое.
Из элементов обучающего множества по методу скользящего окна формируются примеры для обучения нейронной сети. Этот метод подразумевает использование окон Wi и W0 с фиксированными размерами pi и p0. Для описываемой в работе модели размерность выходного слоя нейронной сети совпадает с размерностью выходного окна p0=1. Размерность входного слоя совпадает с размерностью входного окна pi=5, что соответствует продолжительности торговой недели на фондовой бирже. Таким образом, обучающее множество в данной работе состоит из 218 примеров.
 После завершения обучения нейронной сети на примерах из обучающего множества проверяется качество прогноза на элементах тестового множества. Для этого вычисляется ошибка прогнозирования нейронной сети по формуле
После завершения обучения нейронной сети на примерах из обучающего множества проверяется качество прогноза на элементах тестового множества. Для этого вычисляется ошибка прогнозирования нейронной сети по формуле  , где N=25 – размерность тестового множества;
, где N=25 – размерность тестового множества;  – прогнозируемое значение для t-го тестового значения zt.
– прогнозируемое значение для t-го тестового значения zt.
Выбор оптимальной архитектуры нейронной сети и параметров скорости обучения h и момента a не имеет математического решения и производится опытным путем.
Проведенный численный эксперимент показал, что оптимальные значения параметров скорости обучения и момента для рассматриваемого временного ряда hопт, aоптÎ(0,1; 0,5). Когда параметр момента a=0, оптимальное значение параметра скорости обучения hопт®1. Также отметим, что конечная среднеквадратическая ошибка мало отличается для разных кривых, а это означает, что поверхность ошибок в рассматриваемой задаче достаточно гладкая.
Согласно результатам проведенных исследований, оптимальная нейронная сеть для рассматриваемой задачи содержит два скрытых слоя. Входной слой состоит из 5 нейронов; на первом скрытом слое находится 10 нейронов, на втором – 15, а выходной слой содержит 1 нейрон.
Значения основных параметров нейросетевой модели приведены в таблице.
|
Название параметра
|
Значение параметра
|
|
Диапазон начальных значений весовых коэффициентов
|

|
|
Коэффициент скорости обучения h
|
0,5
|
|
Момент a
|
0,1
|
|
Точность обучения e
|
0,005
|
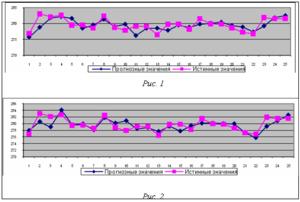
Для нейронной сети, обученной по алгоритму обратного распространения ошибки с целевым функционалом (5) средняя ошибка прогнозирования на тестовом множестве E=0,4487 %, точность прогноза направления тренда составила 52 %. Результаты прогнозирования для нейронной сети данной архитектуры приведены на рисунке 1.
Для нейронной сети, обученной по алгоритму обратного распространения ошибки с целевым функционалом (6), где параметр b=0,5, средняя ошибка прогнозирования на тестовом множестве E=0,4106 %, точность прогноза направления тренда составила 76 %. Результаты прогнозирования для нейронной сети данной архитектуры приведены на рисунке 2.
Результаты применения построенной в работе нейросетевой модели для прогнозирования динамики временного ряда котировок акций компании «Ростелеком» показывают, что нейронные сети могут служить эффективным инструментом для прогнозирования временных рядов финансовых данных. Для всех рассмотренных в работе комбинаций значений параметров нейросетевой модели ошибка прогноза не превышает 0,5 %, что соответствует прогнозу высокого качества.
Предложенная в работе модификация целевого функционала для алгоритма обратного распространения введением в него штрафного коэффициента позволила добиться существенного повышения качества прогноза в направлении тренда, что будет способствовать извлечению прибыли от сделок на фондовом рынке.
Программный продукт, реализованный на базе описанной нейросетевой модели, с успехом применяется в ОАО «ГУТА-БАНК» (г. Тверь) для принятия инвестиционных решений на фондовом рынке.
Литература
1. Хайкин С. Нейронные сети: полный курс; пер. с англ. М.: Издат. дом «Вильямс», 2006. 1104 с.
2. Luo Z. On the convergence of the LMS algorithm with adaptive learning rate for linear feedforward networks. Neural Computation. 1991, vol. 3, pp. 226–245.
3. Рынок акций, котировки акций, рынок ценных бумаг, акции, брокеры и брокерское обслуживание в России. URL: http://stocks.investfunds.ru (дата обращения: 06.07.2009).
4. Kramer A.H. and A. Sangiovanni-Vincentelli. Efficient parallel learning algorithms for neural networks, Advances in neural Information Processing Systems. San Mateo, CA: Morgan Kaufmann. 1989, vol. 1, pp. 40–48.
5. Ширяев А.Н. Основы стохастической финансовой математики. Т. 1. Факты. Модели. М.: ФАЗИС, 1998. 512 с.



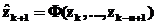 , где
, где  – некоторая нелинейная функция;
– некоторая нелинейная функция;  – прогнозируемое значение ряда;
– прогнозируемое значение ряда;  – наблюдаемые значения (предыстория ряда); n – порядок модели.
– наблюдаемые значения (предыстория ряда); n – порядок модели. и желаемых откликов
и желаемых откликов  . Тем не менее, из теоремы не следует, что один скрытый слой является оптимальным относительно времени обучения, простоты реализации, а также качества обобщения [1].
. Тем не менее, из теоремы не следует, что один скрытый слой является оптимальным относительно времени обучения, простоты реализации, а также качества обобщения [1]. – синаптический вес, связывающий выход нейрона i со входом нейрона j на итерации n;
– синаптический вес, связывающий выход нейрона i со входом нейрона j на итерации n;  – функциональный сигнал, генерируемый на выходе нейрона i на итерации n. Пусть на нейрон j поступает поток сигналов от нейронов, расположенных в предыдущем слое, тогда индуцированное локальное поле
– функциональный сигнал, генерируемый на выходе нейрона i на итерации n. Пусть на нейрон j поступает поток сигналов от нейронов, расположенных в предыдущем слое, тогда индуцированное локальное поле  , полученное на входе функции активации, связанной с данным нейроном, вычисляется по формуле
, полученное на входе функции активации, связанной с данным нейроном, вычисляется по формуле , (1)
, (1) на выходе нейрона j на итерации n равен
на выходе нейрона j на итерации n равен , (2)
, (2) , (a, b)>0, (3)
, (a, b)>0, (3) , где x(n) – входной вектор, поступающий на вход сети; d(n) – желаемый отклик; N – общее число примеров.
, где x(n) – входной вектор, поступающий на вход сети; d(n) – желаемый отклик; N – общее число примеров. (4)
(4) h – параметр скорости обучения; a – постоянная момента;
h – параметр скорости обучения; a – постоянная момента;  – сигнал ошибки выходного нейрона j на итерации n (соответствующий n-му примеру обучения) [1].
– сигнал ошибки выходного нейрона j на итерации n (соответствующий n-му примеру обучения) [1]. , (5)
, (5) – прогнозное значение.
– прогнозное значение. , (6)
, (6) bÎ(0,1).
bÎ(0,1). ,
,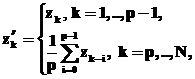 (7)
(7)
 , ведущие себя более однородно, что особенно важно для длительных временных рядов, когда уже заметно влияние инфляции. Величины hn интерпретируются как «возврат», «отдача», «логарифмическая прибыль» [5].
, ведущие себя более однородно, что особенно важно для длительных временных рядов, когда уже заметно влияние инфляции. Величины hn интерпретируются как «возврат», «отдача», «логарифмическая прибыль» [5].
 , где N=25 – размерность тестового множества;
, где N=25 – размерность тестового множества;  – прогнозируемое значение для t-го тестового значения zt.
– прогнозируемое значение для t-го тестового значения zt.
