Проектирование изделий электронной техники (ИЭТ) включает в себя решение многочисленных задач, таких как разработка и проектирование логической и принципиальной электрической схемы ИЭТ, трассировка сигнальных проводников в слоях многослойной печатной платы (МПП), выбор и/или конструирование микросхем (МС), тепловое проектирование ИЭТ и многие другие.
 Одной из основных структурных единиц ИЭТ является электронный модуль (ЭМ), содержащий МПП и установленные на ней МС и электрорадиоэлементы (ЭРЭ) (рис. 1). В силу значительной температурной зависимости электрических параметров МС и ЭРЭ возникновение в конструкции ЭМ температурного поля приводит к тому, что важнейшие электрические характеристики ЭМ – статические и динамические электрические параметры, надежность, быстродействие, помехоустойчивость и т.д. – претерпевают существенные изменения. Поэтому снижение уровней температуры на элементах ЭМ является чрезвычайно актуальной задачей, для чего разработчиками предпринимаются различные меры:
Одной из основных структурных единиц ИЭТ является электронный модуль (ЭМ), содержащий МПП и установленные на ней МС и электрорадиоэлементы (ЭРЭ) (рис. 1). В силу значительной температурной зависимости электрических параметров МС и ЭРЭ возникновение в конструкции ЭМ температурного поля приводит к тому, что важнейшие электрические характеристики ЭМ – статические и динамические электрические параметры, надежность, быстродействие, помехоустойчивость и т.д. – претерпевают существенные изменения. Поэтому снижение уровней температуры на элементах ЭМ является чрезвычайно актуальной задачей, для чего разработчиками предпринимаются различные меры:
- понижение рассеиваемых в МС мощностей,
- применение корпусов МС с малым тепловым сопротивлением,
- установка на корпуса МС теплоотводов (радиаторов),
- интенсификация теплообмена путем установки высокотеплопроводных шин, тепловых труб, применения обдува вентиляторами, жидкостного охлаждения и т.д.
Для эффективного отвода тепловой энергии в конструкциях ЭМ и обеспечения требуемого теплового режима необходимо прежде всего провести тепловое проектирование, которое включает в себя решение следующих задач:
- моделирование (математическое и компьютерное) температурных полей конструкции ЭМ и ее элементов в различных условиях эксплуатации и испытаний;
- проектирование элементов и систем отвода теплоты (конвективно-воздушного, кондуктивно-воздушного, кондуктивно-жидкостного, кондуктивно-испарительного, жидкостного и т.д.);
- конструирование системы эффективного охлаждения элементов ЭМ и всей конструкции ЭМ в целом.
Для того чтобы проектирование и конструирование элементов и систем отвода теплоты в конструкциях ЭМ было возможным, необходимо располагать эффективными универсальными и надежными методами математического и компьютерного моделирования температурных полей сложных конструкций ЭМ, которые должны учитывать следующее.
· Конструкция ЭМ представляет собой сложную систему, состоящую из большого числа элементов, многие из которых сами, в свою очередь, являются сложными системами. Так, конструкция микросхемы состоит из кристалла с созданной на его поверхности системой p-n-переходов, металлизированной разводки, корпуса МС, выводов кристалла и корпуса, элементов теплоотвода и охлаждения.
· Элементы ЭМ характеризуются различными значениями потребляемых мощностей, размерами и пространственной конфигурацией, различными теплофизическими характеристиками материалов, неоднородными включениями и полостями, нестационарным распределением потребляемых элементами мощностей как во времени, так и в пространстве и т.д.
·  МПП и МС, определяющие работоспособность и эксплуатационные характеристики ЭМ, представляют собой многослойные структуры, состоящие из большого числа слоев различной толщины и выполненные из разнородных материалов.
МПП и МС, определяющие работоспособность и эксплуатационные характеристики ЭМ, представляют собой многослойные структуры, состоящие из большого числа слоев различной толщины и выполненные из разнородных материалов.
В статье рассматривается метод математического и компьютерного моделирования трехмерных температурных полей сложных конструкций ЭМ с заранее заданной точностью, учитывающих реальные конструктивные особенности корпусов МС, условия их монтажа на поверхности МПП, особенности крепления МПП в ЭМ, блоках и панелях, конструкции отвода теплоты от элементов ЭМ. Для проведения компьютерного моделирования температурных полей ЭМ разработан программный комплекс на языке Delphi для персональных компьютеров, который не имеет аналогов в российской и зарубежной практике теплового проектирования ЭМ. В отличие от существующих программных комплексов моделирования температурных полей в ЭМ (Beta-Soft, АСОНИКА и др.) количество слоев в МПП, количество МС и ЭРЭ не ограничено.
Моделирование ЭМ
Тепловые модели элементов ЭМ. Элементы ЭМ, установленные на МПП, делятся на активные, характеризующиеся внутренним тепловыделением (МС, диоды, транзисторы, резисторы, катушки индуктивности, трансформаторы), и пассивные, не обладающие собственным тепловыделением (электрические разъемы, конденсаторы, теплоотводы, металлические детали, тепловые трубы). При моделировании теплообмена пассивные элементы выполняют функции теплоотводов и по своей физике являются стоками теплоты, а активные элементы, выделяющие тепловую энергию, – источниками теплоты.
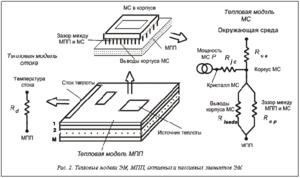
Активные и пассивные элементы моделируются посредством тепловых схем (рис. 2), получаемых методом электротепловой аналогии [1]. Для активных элементов (МС) мощность, потребляемая ими и полностью рассеиваемая в виде тепловой энергии, моделируется независимым источником потока теплоты мощностью Р; тепловой тракт от кристалла МС к корпусу моделируется тепловым сопротивлением переход–корпус Rjc (junction-case); конвективный теплообмен с поверхности корпуса МС в среду или с поверхности корпуса через теплоотвод, установленный на МС, в среду моделируется тепловым сопротивлением корпус–среда Rca (case-ambient); теплопередача от основания корпуса МС к поверхности МПП моделируется двумя, параллельно соединенными тепловыми сопротивлениями, причем Rleads моделирует передачу теплового потока через выводы корпуса (leads – выводы), а Rcp – передачу теплового потока от корпуса МС к плате через зазор между корпусом МС и МПП (cp – case-plate). Тепловые сопротивления Rjc и Rca приводятся в справочных данных на МС, и их значения могут быть также получены моделированием или экспериментально. Для адекватного моделирования активных элементов, установленных на поверхностях МПП, необходимо учитывать, что между элементом ЭМ и поверхностью МПП в пределах площадки, соответствующей элементу, конвективный теплообмен со средой отсутствует. Тепловая модель пассивных элементов ЭМ содержит одно тепловое сопротивление Rd (рис. 2), моделирующее полный тепловой тракт, вдоль которого тепловая энергия отводится от МПП, далее через конструкцию пассивного элемента к стоку теплоты в конце тракта, имеющего температуру Tcd, которая в общем случае может отличаться от температуры среды около МПП.
Тепловая модель МПП представляет собой многослойную структуру (рис. 2), состоящую из множества тонких разнородных слоев различной толщины, количество которых достигает нескольких десятков. С верхней и нижней поверхностей многослойной структуры МПП происходит конвективный теплообмен в среду.
Слои в многослойной структуре МПП могут быть четырех видов: диэлектрические полиимидные слои с теплопроводностью; медные энергетические слои для земли и питания; сигнальные слои с металлическими сигнальными проводниками прямоугольного сечения, разделенные диэлектриком; теплоотводящие, сравнительно толстые медные слои.
Тепловая модель многослойной структуры МПП и реальная конструкция МПП полностью совпадают и представляют собой многослойный прямоугольный параллелепипед (рис. 2) толщиной d и размерами Lx и Ly по осям X и Y, имеющий М слоев, при этом каждый i-й слой (i=1, 2, …, M) имеет толщину di (d=d1+d2+¼+dM) и коэффициент теплопроводности λi, Вт/м·К.
Помимо слоев, выполненных из однородных материалов, реальная конструкция МПП включает в себя сигнальные слои, которые имеют композитную структуру, состоящую из сигнальных металлических проводников прямоугольного сечения и диэлектрических слоев. Расположение сигнальных проводников в слое диэлектрика соответствует маршруту их трассировки, различному для разных слоев, поэтому теплопроводность композитного слоя является анизотропной и различной в каждой точке слоя и вдоль осей X и Y.
Для того чтобы моделирование температурных полей композитных слоев МПП было возможным, необходимо от анизотропной теплопроводности слоя перейти к эффективной усредненной величине теплопроводности lэфф. Концентрация металлических проводников в слое и их местоположение изменяются от слоя к слою и поэтому являются стохастическими с точки зрения МПП, что делает задачу определения эффективной теплопроводности каждого слоя довольно сложной.
Однако в ряде случаев расчет величины lэфф тепловой модели МПП с достаточной для практики точностью можно проводить по формуле ожидаемой величины lэфф=a1 l1+a2 l2, a1+a2=1, где l1 и l2 – теплопроводности металлического проводника и диэлектрика, занимающих в объеме композитного слоя доли, равные a1 и a2 соответственно.
На верхней и нижней сторонах тепловой модели МПП расположены прямоугольные площадки, соответствующие активным и пассивным элементам ЭМ. Для общности моделирования принято, что температура среды и условия теплообмена на верхней и нижней поверхностях МПП различны. Зависимость теплофизических параметров материалов тепловой модели, а также мощностей активных элементов ЭМ от температуры не учитывается.
Математическая модель теплообмена в тепловой модели МПП. Математическая модель, описывающая трехмерное стационарное температурное поле Ti=Ti(x, y, z) в каждом i-м слое тепловой модели МПП, представляет собой систему уравнений.
· Уравнение теплопроводности в i-м слое
 , i=1, 2, …, M.
, i=1, 2, …, M.
· Граничные условия на верхней (i=1) и нижней (i=M) поверхностях тепловой модели МПП, с которых происходит теплообмен в среду по закону Ньютона, одновременное поступление тепловой энергии через источники теплоты в МПП и отвод тепловой энергии от стоков теплоты, расположенных на поверхностях МПП, суммарная мощность которых равна Р1 для i=1 (верхний слой МПП) и РМ – для i=М (нижний слой МПП):
 ,
,
 ,
,
 ,
,  .
.
· Граничные условия на границе i-го и i+1-го слоев тепловой модели МПП, выражающие равенство температур и потоков теплоты на стыке двух соседних слоев:
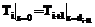 ,
,  .
.
· Адиабатические граничные условия на боковых торцах тепловой модели МПП, полученные в результате допущения о пренебрежимо малом конвективном теплообмене с торцов МПП по сравнению с конвекцией с поверхностей (верхней и нижней) МПП:
 ,
,
где Pj1, PjM – мощности j-го источника (s) или стока (d) теплоты на верхней и нижней поверхностях тепловой модели МПП с размерами по осям X и Y, равными  и
и  соответственно; a1, aM и Ta1, TaM – коэффициенты теплоотдачи и температуры среды с верхней и нижней поверхностей тепловой модели МПП; hj – функция Хевисайда, равная 1, если точка на поверхностях тепловой модели МПП с координатами (xj, yj) принадлежит источнику теплоты, и равная 0 в противном случае, то есть hj=1, если (xj, yj)ÎPj, и hj=0, если (xj, yj)ÏPj.
соответственно; a1, aM и Ta1, TaM – коэффициенты теплоотдачи и температуры среды с верхней и нижней поверхностей тепловой модели МПП; hj – функция Хевисайда, равная 1, если точка на поверхностях тепловой модели МПП с координатами (xj, yj) принадлежит источнику теплоты, и равная 0 в противном случае, то есть hj=1, если (xj, yj)ÎPj, и hj=0, если (xj, yj)ÏPj.
Особенность математической модели ЭМ состоит в том, что температура в произвольной точке тепловой модели ЭМ зависит от мощностей, поступающих в МПП от активных элементов через источники теплоты, а также мощностей, которые отводятся от МПП через пассивные элементы, то есть через стоки теплоты. В то же время мощности в источниках и стоках теплоты зависят от температур, усредненных по площади источников и стоков. Поэтому для того чтобы иметь возможность моделирования температурного поля в любой точке конструкции ЭМ, необходимо прежде всего выразить средние по площади источников и стоков температуры через мощности источников и стоков теплоты, которые сами, в свою очередь, зависят от искомых значений средних температур источников и стоков.
Математическая модель теплообмена конструкции ЭМ может быть записана в матричном виде:  , Ps=AP+B (Ts–Ta), Pd=C(Td–Tcd), в которой Ts=
, Ps=AP+B (Ts–Ta), Pd=C(Td–Tcd), в которой Ts= , Td=
, Td= , Ps=
, Ps= , Pd=
, Pd= – векторы температур, усредненных по площадям источников теплоты Ts и стоков теплоты Td, и векторы мощностей источников Ps и стоков Pd теплоты, расположенных на поверхностях МПП; Rss, Rsd, Rds и Rdd – квадратные и симметрические матрицы, выражающие тепловое взаимодействие между всеми источниками теплоты (Rss), между всеми источниками и стоками теплоты (Rsd), между всеми стоками и источниками теплоты (Rds) и между всеми стоками теплоты (Rdd). Элементы матриц известны априори и рассчитываются на основе точного аналитического решения, получаемого методом двойного косинус-преобразования Фурье [2]; матрицы А, В и С диагональные; Ta=
– векторы температур, усредненных по площадям источников теплоты Ts и стоков теплоты Td, и векторы мощностей источников Ps и стоков Pd теплоты, расположенных на поверхностях МПП; Rss, Rsd, Rds и Rdd – квадратные и симметрические матрицы, выражающие тепловое взаимодействие между всеми источниками теплоты (Rss), между всеми источниками и стоками теплоты (Rsd), между всеми стоками и источниками теплоты (Rds) и между всеми стоками теплоты (Rdd). Элементы матриц известны априори и рассчитываются на основе точного аналитического решения, получаемого методом двойного косинус-преобразования Фурье [2]; матрицы А, В и С диагональные; Ta= , Tcd=
, Tcd= , P=
, P= – векторы заданных и известных априори температур среды, температур охлаждения стоков и мощностей P, потребляемых активными элементами.
– векторы заданных и известных априори температур среды, температур охлаждения стоков и мощностей P, потребляемых активными элементами.
Конечной целью решения матричной математической модели ЭМ является определение мощностей всех источников Ps и стоков Pd теплоты, расположенных на тепловой модели МПП, а после того как они будут найдены, определение искомых значений температур в любой точке конструкции ЭМ, то есть в любой точке МПП на активных и пассивных элементах (кристаллах МС, корпусах МС и т.д.), а также значений температур, усредненных по площадям источников и стоков теплоты. В математической модели известными величинами являются: блочная матрица с матрицами-блоками Rss, Rsd, Rds, Rdd; элементы матриц А, В и С; векторы температуры среды Ta и температуры охлаждения стоков Tcd; вектор мощностей P активных элементов ЭМ. Неизвестными величинами, подлежащими определению, являются: векторы усредненных температур источников Ts и стоков Td; векторы мощностей источников теплоты на МПП Ps и мощностей стоков теплоты на МПП Pd.
В математической модели теплообмена конструкции ЭМ векторы усредненных температур источников Ts и стоков Td зависят от неизвестных значений мощностей источников Ps и стоков Pd, а те, в свою очередь, от неизвестных усредненных температур источников Ts и стоков Td. Блочная матрица математической модели, состоящая из матриц Rss, Rsd, Rds, Rdd, как правило, плохо обусловлена, поэтому использование точных методов для решения уравнений математической модели не всегда приводит к правильному решению, неэффективно и неустойчиво.
Авторами разработан новый метод решения уравнений математической модели, который эффективно достигает цели как для плохо обусловленных матриц, так и для матриц, норма которых больше единицы. В первом случае обычные методы не позволяют найти решение уравнений из-за проблем с устойчивостью и расходимостью, а во втором – используемые итерационные методы расходятся. Предложенный численный метод решения уравнений математической модели основан на идее последовательных приближений и использует комбинацию методов релаксации и половинного деления [3]. Моделирование, проведенное для различных конструкций ЭМ с помощью разработанного метода, показало его эффективность, быструю сходимость к искомому решению (в ряде случаев за 3–5 итераций), а также независимость метода от меры обусловленности матрицы системы уравнений математической модели.
Литература
1. Мадера А.Г. Моделирование теплообмена в технических системах. М.: НФ им. акад. В.А. Мельникова, 2005.
2. Кандалов П.И., Мадера А.Г. Моделирование температурных полей в многослойных структурах // Программные продукты и системы. 2008. № 4 (84). С. 46–49.
3. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.: Физматгиз, 1960.



 , i=1, 2, …, M.
, i=1, 2, …, M. ,
, ,
, ,
,  .
.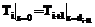 ,
,  .
. ,
, и
и  соответственно; a1, aM и Ta1, TaM – коэффициенты теплоотдачи и температуры среды с верхней и нижней поверхностей тепловой модели МПП; hj – функция Хевисайда, равная 1, если точка на поверхностях тепловой модели МПП с координатами (xj, yj) принадлежит источнику теплоты, и равная 0 в противном случае, то есть hj=1, если (xj, yj)ÎPj, и hj=0, если (xj, yj)ÏPj.
соответственно; a1, aM и Ta1, TaM – коэффициенты теплоотдачи и температуры среды с верхней и нижней поверхностей тепловой модели МПП; hj – функция Хевисайда, равная 1, если точка на поверхностях тепловой модели МПП с координатами (xj, yj) принадлежит источнику теплоты, и равная 0 в противном случае, то есть hj=1, если (xj, yj)ÎPj, и hj=0, если (xj, yj)ÏPj. , Ps=AP+B (Ts–Ta), Pd=C(Td–Tcd), в которой Ts=
, Ps=AP+B (Ts–Ta), Pd=C(Td–Tcd), в которой Ts= , Td=
, Td= , Ps=
, Ps= , Pd=
, Pd= – векторы температур, усредненных по площадям источников теплоты Ts и стоков теплоты Td, и векторы мощностей источников Ps и стоков Pd теплоты, расположенных на поверхностях МПП; Rss, Rsd, Rds и Rdd – квадратные и симметрические матрицы, выражающие тепловое взаимодействие между всеми источниками теплоты (Rss), между всеми источниками и стоками теплоты (Rsd), между всеми стоками и источниками теплоты (Rds) и между всеми стоками теплоты (Rdd). Элементы матриц известны априори и рассчитываются на основе точного аналитического решения, получаемого методом двойного косинус-преобразования Фурье [2]; матрицы А, В и С диагональные; Ta=
– векторы температур, усредненных по площадям источников теплоты Ts и стоков теплоты Td, и векторы мощностей источников Ps и стоков Pd теплоты, расположенных на поверхностях МПП; Rss, Rsd, Rds и Rdd – квадратные и симметрические матрицы, выражающие тепловое взаимодействие между всеми источниками теплоты (Rss), между всеми источниками и стоками теплоты (Rsd), между всеми стоками и источниками теплоты (Rds) и между всеми стоками теплоты (Rdd). Элементы матриц известны априори и рассчитываются на основе точного аналитического решения, получаемого методом двойного косинус-преобразования Фурье [2]; матрицы А, В и С диагональные; Ta= , Tcd=
, Tcd= , P=
, P= – векторы заданных и известных априори температур среды, температур охлаждения стоков и мощностей P, потребляемых активными элементами.
– векторы заданных и известных априори температур среды, температур охлаждения стоков и мощностей P, потребляемых активными элементами.