Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Вариант алгоритма нахождения ошибок для БЧХ-кодов
Аннотация:Описывается вариант алгоритма нахождения позиций ошибок при декодировании двоичных кодов БЧХ. Пред-лагается процедура, основанная на операциях над полиномами, являющаяся альтернативой процедуре Ченя и после-дующему инвертированию ошибочных битов.
Abstract:The variant of the error positions detecting algorithm for binary BCH-codes decoding is described. Proposed procedure, based on polynomial operations, is alternative to the Chen procedure and subsequent error bits inverting.
| Авторы: Громова А.Н. (ganechkaaa@yandex.ru) - Петербургский государственный университет путей сообщения, Алексеев М.О. (alexeevmo@gmail.com) - Санкт-Петербургский университет аэрокосмического приборостроения | |
| Ключевые слова: кратность корня, полиномы над конечным полем, позиции ошибок, локаторный полином, процедура ченя, коды бчх, кодирование |
|
| Keywords: order of root, polynomials over finite field, error positions, locator polynomial, Chen procedure, BCH-codes, FEC |
|
| Количество просмотров: 14083 |
Версия для печати Выпуск в формате PDF (4.97Мб) Скачать обложку в формате PDF (1.38Мб) |
Одним из эффективных способов помехоустойчивого кодирования данных является использование линейных циклических кодов, в частности, кодов БЧХ [1–3]. Рассмотрим двоичный БЧХ-код со следующими параметрами: n – длина кода; k – количество информационных символов; r=n-k – количество проверочных символов, добавляемых в результате кодирования. Порождающий полином этого кода, имеющий степень r, обозначается через g(x). Его коэффициенты лежат в конечном поле GF(2). Обозначим через 2td количество подряд идущих степеней элемента a поля GF(2m): ab, ab+1, …, Пусть требуется передать сообщение Полином c(x), соответствующий кодовому слову, вычисляется по следующей формуле:
Кодовое слово В случае возникновения ошибок в канале связи принятый вектор можно записать как
Множество На приемной стороне необходимо выполнить декодирование вектора По принятому вектору вычисляем синдромный многочлен, определенный следующим образом:
Введем многочлен локаторов ошибок
корни которого обратны локаторам ошибок, определенным выше. Ключевым уравнением декодирования называется уравнение вида
где W(x) – многочлен значений ошибок [3]. Результатом решения ключевого уравнения является нахождение полинома локаторов ошибок L(x), определенного выше. В данной статье предлагается процедура, альтернативная методу Ченя [1, 3] и последующему исправлению ошибочных битов. Рассмотрим ее более подробно. По принятому вектору
где kp – номера ненулевых позиций принятого вектора Вычисляем многочлен L(x) как произведение локаторного полинома b(x) и полинома локаторов ошибок L(x) в поле GF(2m):
Очевидно, что корнями полученного полинома являются корни и локаторного полинома, и полинома локаторов ошибок. В общем случае возможно частичное или полное пересечение множеств их корней. Очевидно, что каждый из полиномов не может иметь два и более одинаковых корней. Из этого следует, что максимальная кратность корней полинома L(x) равна двум. Рассмотрим возможные варианты. 1-й вариант: a-i является корнем полинома L(x) кратности два только в том случае, если a-i является корнем и L(x), и b(x). Другими словами, в разложении L(x) на множители присутствует (1+aix)2. Из принципов построения локаторного полинома и полинома локаторов ошибок следует, что в принятом слове на позиции i одновременно расположена единица и произошла ошибка, то есть Исходя из 2-й вариант: a-i является корнем L(x) кратности один только в случае, если a-i является корнем либо L(x), либо b(x). Это означает, что множитель (1+aix) встречается один раз при факторизации L(x). Другими словами, на позиции i принятого слова либо расположен единичный бит, либо произошла ошибка, то есть Решение о передаваемом символе в любом из этих случаев принимается следующим образом: 3-й вариант: a-i не является корнем полинома L(x) в том случае, если ни L(x), ни b(x) не имеют такого корня. Это означает, что (1+aix) не делит L(x). В этом случае на позиции i одновременно расположен нулевой бит и не произошло ошибки, то есть Очевидно, что при таком условии передавался нулевой бит, так как Описанное свойство полинома L(x) удобно использовать в процессе декодирования. Далее приведен один из возможных алгоритмов, обладающий наименьшей сложностью. Он основан на нахождении корней полинома L(x) и определении их кратности через деление на выражение вида (1+aix)j, где i=0, …, n-1, jÎ{1, 2}. Рассмотрим предлагаемый алгоритм. Шаг 1. Для i=0, …, n-1 вычисляем остаток от деления полинома L(x) на (1+aix)2. Если он равен нулю для некоторого i, то a-i – корень кратности два. В этом случае, как было отмечено ранее, Шаг 2. Выявим корни кратности один. Для всех i, для которых был получен ненулевой остаток на предыдущем шаге, необходимо выполнить его деление на (1+aix). Деление нацело в этом случае является признаком корня кратности один. Следовательно, для таких i Все остальные символы кодового слова Рассмотрим пример работы алгоритма. Пусть используется БЧХ-код (15, 7, 5) над полем GF(24). Поле задается примитивным неприводимым полиномом f(x)=1+x+x4. Порождающий полином кода выглядит следующим образом: g(x)=1+x4+x6+x7+x8. Пусть требуется передать сообщение Вычисленный синдромный полином имеет вид S(x)=a11+a7x+a4x2+a14x3. В результате решения ключевого уравнения и нормировки относительно свободного члена получаем полином локаторов ошибок L(x)=1+a11x+a11x2. Локаторный полином для данного принятого вектора выглядит следующим образом: b(x)=(1+x)(1+ax)(1+a2x)(1+ +a4x)(1+a5x)(1+a6x). Полином L(x), являющийся произведением L(x) и b(x), имеет вид L(x)=1+ +ax2+ax4+a5x5+a2x6+a9x7+a14x8. Выполняем шаг 1 предлагаемого алгоритма. В результате получаем нулевой остаток для i=2, из чего следует, что a-2=a13 является корнем кратности два. Таким образом, Выполняем шаг 2. Деление нацело в данном случае выполняется для i=0, 1, 4, 5, 6, 9. Следовательно, a-i для перечисленных i являются корнями кратности один. Получаем, что Для всех остальных i символы В результате выполнения алгоритма получаем восстановленное слово Легко заметить, что данный алгоритм основан исключительно на операции деления полиномов над конечным полем и операции сравнения. Таким образом, при программной реализации алгоритма достаточно иметь библиотеку для работы с полиномами. При аппаратной реализации деление полиномов может осуществляться с помощью линейных регистров с обратной связью, что обеспечивает невысокие аппаратные затраты. Литература 1. Moon Todd K. Error correction coding: mathematical methods and algorithms. New Jersey: Wiley-Interscience, 2005. 2. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение; пер. с англ. М.: Техносфера, 2005. 3. Кларк Дж.-мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи; пер. с англ. М.: Радио и связь, 1987. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2512&like=1&page=article |
Версия для печати Выпуск в формате PDF (4.97Мб) Скачать обложку в формате PDF (1.38Мб) |
| Статья опубликована в выпуске журнала № 2 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 . Предположим, что они являются корнями полинома g(x) [3].
. Предположим, что они являются корнями полинома g(x) [3].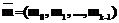 , такое, что miÎGF(2), i=0, …, k-1. Поставим ему в соответствие полином
, такое, что miÎGF(2), i=0, …, k-1. Поставим ему в соответствие полином  . Рассмотрим процесс кодирования данных на передающей стороне.
. Рассмотрим процесс кодирования данных на передающей стороне.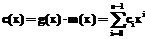 .
. представляет собой вектор коэффициентов многочлена c(x), то есть
представляет собой вектор коэффициентов многочлена c(x), то есть  .
. , где через
, где через  обозначен вектор ошибок длины n. Пусть количество ненулевых компонентов вектора ошибок равно v£td. Перепишем многочлен ошибок следующим образом:
обозначен вектор ошибок длины n. Пусть количество ненулевых компонентов вектора ошибок равно v£td. Перепишем многочлен ошибок следующим образом: .
.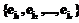 , где ejÎGF(2), соответствует значениям ошибок. Под локатором ошибки будем понимать примитивный элемент поля GF(2m) в степени, равной номеру позиции ошибки. Тогда множество локаторов ошибок можно записать как
, где ejÎGF(2), соответствует значениям ошибок. Под локатором ошибки будем понимать примитивный элемент поля GF(2m) в степени, равной номеру позиции ошибки. Тогда множество локаторов ошибок можно записать как  .
.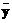 с целью устранения произошедших ошибок. Рассмотрим процедуру декодирования.
с целью устранения произошедших ошибок. Рассмотрим процедуру декодирования.
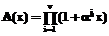 ,
, ,
,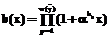 ,
, назовем локаторами единиц принятого вектора
назовем локаторами единиц принятого вектора  . Легко заметить, что корнями полинома b(x) являются элементы поля GF(2m), обратные локаторам единиц.
. Легко заметить, что корнями полинома b(x) являются элементы поля GF(2m), обратные локаторам единиц. .
. .
. , следует, что символ на позиции i восстановленного кодового слова
, следует, что символ на позиции i восстановленного кодового слова  .
.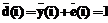 .
. .
.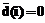 .
.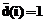 .
. равны нулю, так как для оставшихся i элемент a-i не является корнем полинома L(x).
равны нулю, так как для оставшихся i элемент a-i не является корнем полинома L(x). =(1, 1, 0, 0, 0, 0, 0), которому соответствует полином m(x)=1+x. Полученное кодовое слово
=(1, 1, 0, 0, 0, 0, 0), которому соответствует полином m(x)=1+x. Полученное кодовое слово 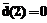 .
. при iÎ{0, 1, 4, 5, 6, 9}.
при iÎ{0, 1, 4, 5, 6, 9}.