Программные продукты и системы

В современных информационных компьютерных системах хранятся и постоянно создаются гигантские объемы информации. Эта информация часто организована средствами естественного языка, а значит, ее реальное освоение возможно при условии автоматической смысловой обработки текстов. Проблема определения смыслового содержания естественно-языковых фрагментов не нова и активно изучается со второй половины XX века [1].

Эффективное использование знаний, содержащихся в текстах, требует новых стратегий обработки информации, отличных от традиционных подходов. Такие стратегии должны учитывать семантические законы естественного языка [2].

Изучение семантики предложения тесно связано с мышлением. Поэтому исторически первые попытки формализации методов работы с семантикой предпринимались в рамках логики. Логический подход к формализации семантического анализа до недавнего времени имел распространение лишь в среде лингвистов и логиков. Авторам представляется перспективным применение логического подхода к проблеме автоматизации обработки естественно-языковых текстов с помощью ЭВМ. Выделим основные плюсы такого подхода.

Простое распараллеливание единой задачи. Символьные формулы достаточно просто дробятся на подформулы. Выводимость отдельной подформулы чаще всего можно проверять независимо от других. Это свойство особенно важно ввиду движения современной вычислительной техники в сторону многоядерности микропроцессоров и распределенной обработки данных.

Множественность решаемых задач на едином наборе знаний. Логическое представление позволяет на едином наборе данных/знаний производить различные операции. Так, на одной базе могут функционировать поисковые системы, вопросно-ответные системы, системы распознавания образов и т.д.

Естественное объяснение результатов операций. Логика формализует правила мышления, поэтому результаты набора логических операций при достаточной дружественности пользовательского интерфейса могут легко пониматься пользователем. В логической поисковой системе можно показать цепочку умозаключений, на основе которой предлагаемый текст отнесен к релевантным результатам поиска. Большинство существующих методов не дают такой возможности объяснения результата, поскольку наборы векторных и статистических данных, с которыми они работают, гораздо сложнее представить в доступном для неподготовленного пользователя виде. Это достаточно важное обстоятельство, так как опыт использования систем поддержки принятия решений показал, что пользователь чаще всего отвергает результат работы программы, если не может уяснить, каким образом такой результат был получен.

Развитие логического подхода к изучению семантики можно проследить на основе существующих семантик неклассических логик: семантики смысла и денотата Г. Фреге, теории объектов и пропозиций Б. Рассела, теории истины А. Тар­ского, семантики возможных миров С. Крипке, логики смысла и денотата А. Черча. Наиболее перспективным с точки зрения применимости в автоматическом семантическом анализе представляется подход, предложенный Ричардом Монтегю. Он сформировал целое направление, получившее название «формальная семантика». Основная идея работ Монтегю выражена в названии одного из его основополагающих трудов «English as a formal language». Любой естественный язык (в частности английский) предлагается понимать как формальный логический язык, который является более сложным по отношению к существующим формальным языкам. Следовательно, при описании естественного языка можно использовать те же понятия и конструкции, что и для других логических языков.

Центральный принцип формальной семантики заключается в композиционном отношении между синтаксисом и семантикой. Принцип композициональности можно выразить следующим образом: значение выражения есть функция его частей и способа их синтаксической комбинации. При этом истинность определяется не абсолютно, а в пределах некоторой модели [3].

Возможны два подхода к изучению семантико-синтаксических связей:

-    описать синтаксис естественного языка (в нашем случае русского) и интерпретировать выражения языка в моделях;

-    использовать промежуточный логический язык, для чего описать синтаксис и семантику достаточно близкого к естественному логического языка; при этом описание семантики естественного языка сводится к представлению текста в сконструированном логическом языке.

Монтегю использовал оба этих подхода. Для решения целей данной работы второй подход представляется более перспективным, так как позволяет реализовать описанные выше плюсы логического представления языков.

В работе [4] Монтегю использует пару координат – возможные миры и временные промежутки, относительно которых для каждого выражения определяются интенсионал и экстенсионал. Мо- делью для интенсиональной логики Монтегю является пятерка вида: M=áD, W, T£, Iñ, где D – множество индивидов (или несущее множество); W – множество возможных миров; T – множество моментов; £ – отношение порядка, заданное на T; I – интерпретирующая функция, которая придает семантические значения всем константам.

Семантическая интерпретация интенсиональной логики использует множество оценок S={gi½i=1, …. n}, которые являются множеством функций, отображающих переменные всех типов в множества соответствующих значений (g – функция приписывания значения переменной); aM,g – интенсионал выражения относительно модели М и функции приписывания g; aM,w,t,g – экстенсионал выражения α относительно M, g и точки соотнесения áw, tñ, где wÎW, tÎT.

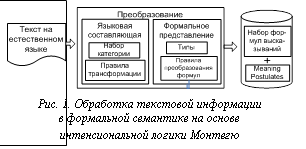
С точки зрения реализации технической системы  можно выделить следующие фрагменты обработки текстовой информации средствами формальной семантики (рис. 1).

Схема наглядно показывает, как происходит функциональное деление частей единой системы под названием «логика Монтегю». В блоке «языковая составляющая» объединены элементы, специфичные для конкретного естественного языка. Формальное представление не зависит от конкретного языка и является единым для многих реализаций языковых составляющих. Сейчас основные исследования сосредоточены в области естественно-языковой составляющей (с внесением необходимых изменений в постулаты значения). На языковую составляющую вводятся ограничения таким образом, чтобы она представляла подмножество естественного языка, минимально необходимое для представления простых языковых фраз.

На данный момент изучение формальной семантики сводится именно к определению способов перехода от естественно-языкового представления к формализованному логическому. Возможны различные способы таких переходов.

В работах Монтегю проводится различие между понятиями тип и категория. Относительно формализованных фрагментов естественного языка употребляется понятие категория. В логических построениях используется понятие тип выражения. Тип выражения задается через рекурсивное определение типов. Определим элементы множества типов TYPE:

1) eÎTYPE,

2) tÎTYPE,

3) если aÎTYPE и bÎTYPE, то áa, bñÎTYPE,

4) если aÎTYPE, то ás, añÎTYPE,

5) ничто, кроме указанного в пп. 1–4, не принадлежит множеству TYPE.

Множество TYPE не является множеством самих выражений. Это множество имен множеств выражений. Типы е и t являются элементарными. Символ е обозначает сущность (entity). Индивидные переменные и индивидные константы имеют тип е. В семантической интерпретации выражениям типа е будут соответствовать объекты из индивидной области.

Символ t используется для обозначения типа формул, то есть выражений, которые могут быть оценены как истинные или ложные. Комбинации элементарных типов образуют все иные типы выражений (бесконечный класс), которые мыслятся как функторы.

Запись <а, b> указывает на тип функции, где а – тип аргумента, b – тип значения функции. Например, одноместный предикат первого порядка есть функция типа <е, t>, аргумент которой имеет тип е, а значение – тип t.

Для связи с естественным языком применяется множество категорий. Определим функцию f для отображений категорий русского языка в логические типы следующим образом [5]:

1) f(e)=e,

2) f(t)=t,

3) f(CN)=f(IV)=,

4) для всех категорий А и В f(A/B)=f(A//B)= =<,f(A)>.

Выражение категории функтора А/В при сочленении с категорией аргументора В дает составное выражение категории целого А. Выражения категории А/В и А//В различаются синтаксически, но не семантически, и соответствуют одному и тому же логическому типу. Основные категории представлены в таблице 1.

Таблица 1

Для перевода категориальных выражений в язык логики используются правила трансформации (ПТ). Монтегю выделяет множество основных выражений категории А, обозначая его через ВА, и множество фраз категории А, обозначая его через РА. Множество РА состоит из основных выражений и тех, которые могут быть получены с помощью синтаксических правил. Синтаксические правила PTQ задают множество РА для каждой категории A.

При рассмотрении естественного языка в качестве формального предполагают, что модели языка отражают те схемы, которые языковое сознание накладывает на мир. В идеальном случае построенная абстракция должна отражать «наивную картину мира» (терминология московской семантической школы).

В то же время в формальной семантике, как и в логике, давно рассматривались meaning postulates (постулаты значения) при описании лексических значений. Сейчас meaning postulates все чаще используются для отражения структурных особенностей лексики. С точки зрения логики meaning postulates – это аксиомы, описывающие соотношения лексических констант для описания словарных значений и наивной картины мира.

Рассмотрим схему перехода от фразы на естественном языке к ее формальному представлению (рис. 2).

1)  Морфологическая и синтаксическая обработка фразы (лингвистическая обработка). Результатом этого этапа должны стать два множества значений. Первое множество, Morph, состоит из пар <слово, характеристики>. Второе множество, Syn, состоит из набора синтаксических клауз, которые выделяются данным анализатором. На втором множестве часто определяют отношения подчиненности, так как синтаксическое построение групп имеет древовидную структуру. При этом определяется функция соотнесения слов с их характеристиками и клауз, которые они составляют. К необходимым характеристикам относятся начальная (нормализованная) форма и часть речи. Возможно выделение других характеристик (род, падеж, переходность и др.). Ни построение такого дерева, ни морфологические характеристики не могут быть оторванными от набора категорий, используемых на следующем этапе.

2) 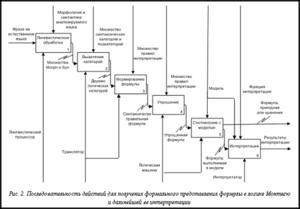 Выделение синтаксических категорий и подкатегорий. Рассмотрение альтернатив. На основе результатов первого пункта рассматриваются категории, принятые к логике, в которую переводится целевое сообщение. При наличии альтернатив выбирается наиболее общий вариант. Категории объединяются в более крупные категории на основе синтаксического дерева. Кроме того, в пределах категорий могут выделяться подкатегории со своими особенностями формализации, постулатами значения и т.д.

3)  Перевод фразы в формулу логики на основе набора категорий и правил трансформации. На основе набора категорий и правил трансформации строится формула логики, являющаяся отображением фразы естественного языка на формальном языке формул.

4)  Упрощение полученной формулы. Полученная на предыдущем этапе формула чаще всего будет достаточно громоздкой. Для уменьшения избыточности, а также для удобства дальнейшей обработки и хранения возможно ее упрощение. В логике Монтегю используется лямбда-исчисление. Поэтому упрощение связано с последовательным применением различных видов редукции и сокращением взаимно уничтожающих друг друга операторов получения интенсионала и экстенсионала выражения. Возможны и другие способы.

5)  Соотнесение полученной формулы с выбранной моделью. Формула должна быть соотнесена с индексом времени и миров, а также с модальными и эпистемическими контекстами, если таковые используются в данной логике. Осуществляются проверка на выполнимость полученной формулы в этой модели и выявление фактов, противоречащих данному сообщению, если это возможно. Результатом этой операции является получение знания о том, что формула не противоречит модели. В таком случае ее можно интерпретировать или добавить в общее хранилище знаний.

6)  Интерпретация полученной формулы в модели. С помощью функции интерпретации формула может получить свое отражение в реальном мире. Например, сообщение на естественном языке может оказаться командой производственной линии. Тогда функция интерпретации должна быть преобразована в набор управляющих сигналов для оборудования.

Как видно из рисунка 1, начальным этапом обработки является преобразование текста на естественном языке на основе языковой составляющей логики. Этот фрагмент преобразования сильно зависит от грамматики и синтаксиса языка изложения текста.

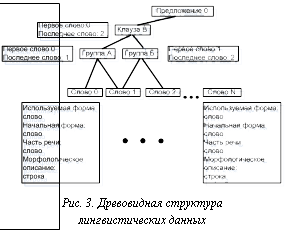В качестве компонента лингвистической обработки используем лингвистический процессор группы aot (www.aot.ru). Данная система лингвистических процессоров распространяется в исходных кодах на языке С++ под ОС Linux. Существует вариант и для Windows в виде набора com-объектов. В этом случае приоритетнее Linux-реализация, так как лингвистический компонент для совместного использования следует поместить на сервере, а наиболее предпочтительны для серверов UNIX-подобные системы. Результатом синтаксического анализа будет являться набор групп и клауз, составляющих предложение (рис. 3).

Суждение о базовых категориях можно выдвигать на основе морфологии слова. Соотношения констант морфологического анализа и категорий логики Монтегю представлены в таблице 2.

Результаты морфологического анализа позволяют представить только атомарные категории логики. Построение составных категорий возможно на основе результатов синтаксического анализа предложения. Соотношения категорий интенсиональной логики и констант выбранного синтаксического анализатора даны в таблице 3.

Результатом приведенной последовательности преобразований является формула, удовлетворяющая синтаксису формул интенсиональной логики. При интерпретации ее в модели получаем истинностное значение предложения на основе семантики, накладываемой функцией интерпретации.

Таблица 2

Таблица 3

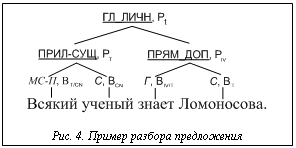
Рассмотрим пример формализации естественно-языкового предложения «Каждый ученый знает Ломоносова». Дерево программного синтаксического анализа, совмещенное с деревом категорий, изображено на рисунке 4 (курсивом выделены морфологические константы, а подчеркиванием – константы синтаксиса).

Рассмотрим пошаговое преобразование выражения. При этом выражение kÞn будем читать как «k переводится в n». Для выражения естественного языка d будем считать d¢ его переводом на язык интенсиональной логики:

1)   Ломоносов Þ l, где l – элемент множества констант предметной области

2)   ученый Þ ученый¢

3)   знает Þ знает¢

4)   каждый ученый ÞlP"x[ученый¢(x)®P{x}], так как согласно правилу перевода, если zÎPCN, zÞz¢, то «каждый (каждая, каждые) z.».ÞlP "x[z¢(x)®P(x)]

5)   x0 знает Ломоносова Þ знает¢(l)(x0)= =lx0[знает¢(l)(x0)], где x0 – индивидная переменная типа

6)   согласно субъектно-предикативному правилу, если αÎPT, dÎPIV, то F4(α, d)ÎPt и переводится в α¢(Ùd¢), где ½Ùα½M,w,t,g есть функция h с областью определения W´T, такая, что для любой пары áw¢, t¢ñ из W´T h(áw¢, t¢ñ)=½α½M,w¢,t¢,g. В данном случае, объединяя 4 и 5, получим lP"x [ученый¢(x)®P{x}](Ùlx0[знает¢(l)(x0)]). Для упрощения программного текстового вывода формулы сделаем следующие замещения l=lambda, "=all, ®=impl. Тогда на выходе программного преобразователя получим lambda P all x(ученый¢(x) impl P{x})(^ lambda x0 (знает¢(l)(x0))

7)   после упрощения получим "x(ученый¢(x)® ®знает¢(l)(x)).

Предлагаемый метод обработки естественно-языковых массивов может быть полезен при заполнении хранилищ знаний, которые в дальнейшем могут использоваться, например, при информационном поиске, реализации вопросно-ответ­ных и экспертных систем.

Литература

1. Арутюнова Н.Д. Предложение и его смысл. Логико-семантические проблемы. М.: Наука, 1976. 383 c.

2. Городецкий Б.Ю. Компьютерная лингвистика: моделирование языкового общения // Новое в зарубежной лингвистике: Вып. XXIV. Компьютерная лингвистика. М.: Прогресс, 1989. 432 с.

3. Микиртумов И.Б. Теория смысла и интенсиональная логика. СПб: Изд-во СПбГУ, 2006. 351 с.

4. Montague R. The proper treatment of quantification in ordinary English // Approaches to Natural Language / Hintikka K.J.J., Moravcsik J.M.E. & Suppes P. (eds.). Reidel, 1973, pp. 221–242.

5. Герасимова И.А. Формальная грамматика и интенсиональная логика. М.: Ин-т филос. РАН, 2000. 156 с.