Разработка численной схемы стекловаренной печи
| Швыдкий В.С. (vshvit@isnet.ru) - Уральский государственный технический университет, г. Екатеринбург, доктор технических наук, Собянин С.Е. (ssergey@pochtamt.ru) - Уральский государственный технический университет, г. Екатеринбург | |
| Ключевые слова: аппроксимация, дискретный аналог, численная схема, стекловаренная печь, математическая модель |
|
| Keywords: approximation, discrete analog, numerical scheme, glass furnace, mathematical model |
|
|
|
|
При разработке численной схемы стекловаренной печи необходимо обязательно учесть особенности стекломассы: большую плотность и вязкость, медленное движение (практически ползущее). Учитывая их, можно уверенно отнести стекломассу к несжимаемой жидкости. Конечно, плотность стекломассы зависит от температуры, а температура в бассейне изменяется, но, во-первых, эта зависимость слабая и, во-вторых, температура стекломассы в ванне изменяется от 1000 до 1580 оС, что приводит к относительно небольшим изменениям плотности. Иными словами, с достаточной точностью можно считать для стекломассы div v=0 и записать уравнения движения в виде: · в проекции на ось x
· в проекции на ось y
· в проекции на ось z
Вязкость стекломассы существенно зависит от температуры. Однако уравнения (1)–(3) – это уравнения баланса импульса для бесконечно малого объема. При составлении этого баланса можно считать, что температура стекломассы, следовательно, и ее вязкость, в пределах элементарного объема одинаковы. Тогда m можно вынести из-под знака производных, что приводит к упрощению уравнений. Например, в уравнении (1) выделим слагаемые
то же сделаем и для уравнений (2) и (3). Заметим, что такой подход не исключает учета зависимости m от температуры, поэтому окончательный вид уравнений движения стекломассы можно представить следующим образом:
Уравнение неразрывности можно упростить. Хотя формально необходимо учитывать наличие внутренних источников (стоков) массы, фактически сделать это нельзя из-за неопределенности кинетики физико-химических превращений и отсутствия математического описания. Поэтому используем уравнение неразрывности в форме
Здесь возникло некоторое противоречие со сделанным утверждением о несжимаемости стекломассы, однако, во-первых, введение плотности под знаки производных не слишком усложняет уравнение, а, во-вторых, это важно для дальнейшего учета теплообмена. Построение дискретного аналога всегда нужно выполнять для безразмерных уравнений, поскольку в этом случае легче оценить порядок аппроксимации и устойчивость численной схемы. Введем соответствующие безразмерные параметры. Предварительно, однако, приведем уравнения движения к дивергентному виду, объединив с уравнением неразрывности:
Отсчитаем компоненты скорости в долях среднерасходной скорости стекломассы в протоке V0=P/(86,4∙r0∙z2∙b2) м/с, где r0 – масштабное значение плотности стекломассы (кг/м3); P – производительность печи, т/сутки; z2 – высота прото- ка, м; b2 – ширина протока, м. Индекс 0 у теплофизических параметров характеризует значение при масштабной температуре T0=1000 оС. В качестве характерной длины выберем длину ванны L. Тогда имеем
Здесь h – глубина слоя стекломассы в ван- не, м; b – ширина ванны, м; x1 – длина загрузочной части ванны, м. Подстановка этих соотношений в консервативную форму записи уравнения движения в проекции на ось x приводит к выражению
или
где P=p/(r0V02) – безразмерное давление, или число Эйлера; Re=r0V0L/m0 – число Рейнольдса; Fr=V02/(gL) – число Фруда. Введем обозначения: F1= H1= F2= H2= F3= H3= Тогда уравнения движения можно переписать в компактном виде:
Для аппроксимации уравнения неразрывности и уравнений системы (8) воспользуемся шахматной, или разнесенной, конечноразностной сеткой. Осуществим переход к разностным соотношениям на различных контрольных объемах (КО). Нужно отметить, что сетка на самом деле едина (в геометрическом плане) и индексация в различных КО изменяется лишь с целью более четкого выделения искомых параметров. В ряде случаев такая условность затрудняет построение дискретных аналогов (возникает неопределенность индексации), поэтому в данной работе следует связать индексацию с геометрическим центром КО, на котором аппроксимируется уравнение неразрывности. В этом центре определим все параметры состояния среды: давление, температуру и концентрацию. Используя контрольный объем, соответствующий данным рисунка 1, запишем уравнение неразрывности в виде
Но по заданному условию теплофизические свойства берутся в центре КО и далее остаются неизменными во всем объеме параллелепипеда. Тогда во всех слагаемых плотность одинакова и, следовательно, исключается из (9). В результате имеем
Можно видеть, что данная форма аппроксимации сохраняет физический смысл уравнения неразрывности как разности между массовыми расходами втекающей в КО и вытекающей из него стекломассы. По сравнению с первоначальной трактовкой изменена индексация компонентов скорости. Согласно физическому смыслу баланса массы определяемыми величинами являются компоненты скорости в геометрическом центре граней, то есть Uj-1/2,k,l, Uj+1/2,k,l, Vj,k-1/2,l, Vj,k+1/2,l, Wj,k,l-1/2 и Wj,k,l+1/2. Перейдем к уравнениям баланса импульсов. В проекции на ось Х имеем
В новой индексации не все суммарные индексы попадают в целочисленные узлы. В соответствии с рисунком 2 координаты КО для оси Х изменяются в пределах: по Х от Xj до Xj+1; по Y от Yk-1/2 до Yk+1/2; по Z от Zl-1/2 до Zl+1/2. Применяя метод контрольного объема к уравнению х-компоненты импульса (8) с КО, показанным на рисун- ке 2, можно получить дискретное уравнение
Центральным параметром данного КО является компонент Uj+1/2,k,l, поэтому все аппроксимации выполняются относительно этой величины. После небольших математических преобразований получим следующее уравнение, записанное в каноническом виде:
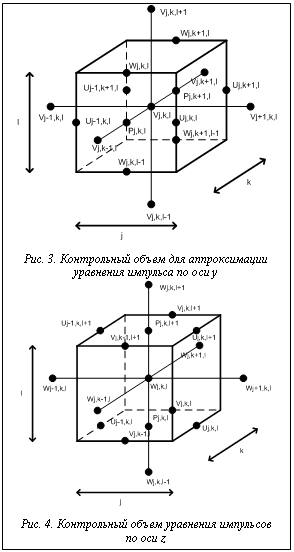
где Можно заметить, что уравнение (11) нелинейно и, следовательно, может быть решено только методом итераций. Теплофизические параметры на гранях КО можно определить либо как среднегеометрическое из соседних узловых значений, либо как среднеарифметическое. Аналогично рассматриваются и другие координатные направления. КО для оси y лежит в диапазоне: по Х – от Xj -1/2 до Xj+1/2; по Y – от Yk до Yk+1; по Z – от Zl–½ до Zl+1/2 (рис. 3). При помощи КО, изображенного на рисунке 3, дискретная форма уравнения y-компоненты импульса (второе уравнение системы (8)) может быть записана в виде
Здесь основной (искомой) переменной является Vj,k+1/2,l. После небольших математических преобразований получим уравнение для оси Y, записанное в канонической форме:
Наконец, в соответствии с КО, представленным на рисунке 4, для z-компоненты импульса (третье уравнение системы (8)) можно записать
В данном случае определяющей величиной является компонента Wj,k,l+1/2, поэтому получаем следующее уравнение для оси Z, записанное в канонической форме:
Подведем итоги. Гидродинамическая часть численной модели на данном этапе включает четыре уравнения: одно уравнение неразрывнос- ти (9а):
и три уравнения баланса импульсов:
Уравнения баланса импульсов дадут верные значения компонентов скорости, превращающие уравнение неразрывности в тождество, лишь в том случае, когда при их решении будет использоваться правильное поле давления. Но даже тогда для решения системы понадобятся граничные условия. Для решения уравнений дискретного аналога можно воспользоваться методом SIMPLE С. Патанкара. В плане граничных условий основную сложность представляет задание компонентов скорости на свободной поверхности. Для неизотермической задачи здесь можно попытаться воспользоваться эффектом Марангони. Однако для изотермического потока этот выход отсутствует, и приходится изыскивать какие-то другие способы. Литература 1. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984. 152 с. 2. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978. 592 с. 3. Дзюзер В.Я., Брылина Т.С., Собянин С.Е. Численное моделирование внешнего теплообмена в газоэлектрической стекловаренной печи с подковообразным направлением пламени // Стекло и керамика. 2008. № 5. С. 8–16. |
http://swsys.ru/index.php?id=2574&lang=%E2%8C%A9%3Den&like=1&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Моделирование программы таксономии технологий изготовления деталей машиностроительного профиля с помощью сетей Петри
- Программный комплекс оптимизации законов управления
- Применение локальных трендов для предподготовки временных рядов в задачах прогнозирования
- Использование программного обеспечения для определения и прогнозирования показателей качества экструдированной продукции
- Математические модели реограмм состояния в программах Table Curve 2d/3d как основа интеллектуальной системы управления процессами структурирования многокомпонентных эластомерных композитов

 (1)
(1) (2)
(2) (3)
(3)




 (4)
(4)

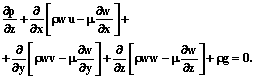




 (5)
(5)
 (6)
(6) (7)
(7) G1=
G1=

 G2=
G2=

 G3=
G3=

 (8)
(8)
 (9)
(9)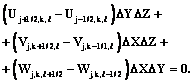 (9а)
(9а)
 (10)
(10) (11)
(11) означает все конвективные и диффузионные вклады из соседних узлов.
означает все конвективные и диффузионные вклады из соседних узлов.
 (12)
(12) (13)
(13)
 (14)
(14) (15)
(15)