Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Построение кодовых слов пространственно-частотно-временных кодов
Аннотация:Предложен сравнительно несложный метод построения кодовых слов пространственно-частотно-временных кодов, приведено его обоснование и рассмотрен пример построения кодового слова пространственно-частотно-временного кода в соответствии с данным методом. Основная идея заключается в построении порождающей матрицы кода по основным характеристикам MIMO-системы.
Abstract:The paper deals with a new method of constructing codeword of space-time-frequency (STF) codes that is less complex compared. The author presents the substantiation of the method and considers the example of constructing a codeword of STF code in accordance with the method proposed. The general idea is to construct a generating matrix code to the main characteristics of the MIMO-systems.
| Автор: Гофман М.В. (maxgof@gmail.com) - Петербургский государственный университет путей сообщения | |
| Ключевые слова: mimo-система, порождающая матрица, пространственно-частотно-временной код |
|
| Keywords: MIMO-system, generator matrix, space-time-frequency code |
|
| Количество просмотров: 11124 |
Версия для печати Выпуск в формате PDF (5.84Мб) Скачать обложку в формате PDF (1.43Мб) |
Методика построения кодового слова для кодов, ориентированных на использование в MIMO-системах, представленная в [1], основана на построении кодовых слов путем объединения независимо кодируемых частей, называемых слоями. Слой представляет собой вектор из комплексных чисел, а кодовое слово – матрицу, каждый элемент которой принадлежит некоторому слою. При объединении слоев в кодовое слово элемент каждого слоя передается в каждый промежуток времени так, что частоты использования каждой передающей антенны (в передаче элементов слоя) равны. Далее методику построения кодовых слов будем называть методикой слоения. Методика слоения была использована в [2] для построения кодовых слов пространственно-частотно-временного кода. Каждое кодовое слово этого кода состоит из нескольких независимо кодируемых блоков. Каждый такой блок строится на основе методики слоения. В дальнейшем, говоря о коде и методике, будем подразумевать под ними пространственно-частотно-временной код и методику построения его кодовых слов (см. [2]). Методика построения пространственно-частотно-временного кодового слова включает выполнение двух действий: построение блоков кодового слова и объединение этих блоков в одно кодовое слово. Покажем, как построить матрицу этих действий, которую назовем порождающей матрицей. Введем следующие обозначения: Характеристики MIMO-системы: Nt – число передающих антенн; Nb – число блоков замираний [1], в течение которых будет передаваться кодовое слово; L – число лучей при распространении сигнала от каждой антенны (будем предполагать, что на каждом из лучей соответствующие задержки во времени одинаковы для всех антенн). Опишем методику построения кодового слова пространственно-частотно-временного кода. Допустим, что имеется некоторый комплексный вектор определенной длины, который необходимо преобразовать в кодовое слово. По методике этот вектор разделяется на части, также представляющие собой векторы. Эти векторы подвергаются одинаковому матричному преобразованию. В результате каждого такого преобразования получается вектор, который определяет блок кодового слова. Если обозначить такой блок через
где J – число блоков в кодовом слове. Предположим, что нужно закодировать Ns=NLNqNtNbJ информационных символов из алфавита По методике построения каждый вектор
Прежде чем дать определение матрицы Qj, сделаем ряд допущений. Пусть FM – матрица дискретного преобразования Фурье размера M´M, где Теперь определим матрицу Qj как матрицу, получаемую путем вырезания первых NLNtNb строк и столбцов из матрицы Yj=Yfj-1. Объединим множество слоев
Далее, говоря об элементе вектора Для построения кодового слова удобно воспользоваться двумя вспомогательными векторами, элемент первого будет показывать номер слоя (вектор слоев), а элемент второго – положение в слое (вектор смещений). Обозначим
где m=1,…,NLNqNtNb. После определения матрицы P весь процесс перестановок элементов вектора В результате получается, что
Зная множество векторов Построение порождающей матрицы Завершив описание методики построения кодового слова, покажем, как построить порождающую матрицу кода. На основе формул (2) и (5) построим матрицу Gi вида Gi=P×diag(Q1 Q2 … QNq), с помощью которой можно заменить весь процесс построения вектора Gcodeword=diag(G1, …, GJ), (6) процесс построения кодового слова можно заменить умножением информационного вектора Матрица Gcodeword называется порождающей матрицей кода. В теории кодов, ориентированных на использование в MIMO-системах, кодовые слова традиционно представляют в виде матриц. Поэтому, чтобы завершить описание рассматриваемого кода, необходимо упомянуть об элементе, называемом форматировщиком, который и выполняет соответствующее преобразование кодового вектора Пример. Параметры MIMO-системы: Nt=2, Nb=2, L=2. Пусть J=2, тогда Ns=NLNqNtNbJ= =2×2×2×2×2=32. Предположим, что необходимо закодировать вектор Обозначим k-й элемент вектора Воспользовавшись выражением (3), получим
и Объединив
Если предположить, что вектор слоев
Используя
и Объединив
Применив форматировщик, настроенный на длину строки, равную 4 элементам, к вектору
Матрица Y соответствует пространственно-частотно-временному кодовому слову для 8 подканалов. Знание порождающей матрицы (6) позволило сократить число действий, необходимых для построения кодового слова пространственно-частотно-временного кода, представленного в [2]. В общем, число действий сократилось до одного умножения справа информационного вектора на порождающую матрицу. Литература 1. Gamal H.El., Damen M.O. Universal Space–Time Coding // IEEE Transactions on Information Theory, V. 49, № 5, pp. 1097–1119, may 2003. 2. Zhang Wei, Xiang-Gen Xia, Ching P.C. High-Rate Full-Diversity Space–Time–Frequency Codes for Broadband MIMO Block-Fading Channels // IEEE Transactions on Communications, V. 55, № 1, january 2007. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2586&page=article |
Версия для печати Выпуск в формате PDF (5.84Мб) Скачать обложку в формате PDF (1.43Мб) |
| Статья опубликована в выпуске журнала № 3 за 2010 год. |
Назад, к списку статей



 – множество положительных целых чисел;
– множество положительных целых чисел;  – кольцо целых чисел;
– кольцо целых чисел;  – поле рациональных чисел;
– поле рациональных чисел;  ;
;  – вектор-столбец a; T, H – обычное транспонирование и транспонирование с сопряжением соответственно; ëxû, éxù – наибольшее целое число, меньшее или равное x, и наименьшее целое число, большее или равное x, соответственно; diag(x0, x1, …, xN-1) – диагональная матрица размера N´N с диагональными элементами, равными x0 x1 … xN-1, если xn – это скаляр, или блоковая диагональная матрица размера NM´NM с матрицами размера M´M на главной диагонали, если xn – это матрица размера M´M, где n=0, 1, … N-1.
– вектор-столбец a; T, H – обычное транспонирование и транспонирование с сопряжением соответственно; ëxû, éxù – наибольшее целое число, меньшее или равное x, и наименьшее целое число, большее или равное x, соответственно; diag(x0, x1, …, xN-1) – диагональная матрица размера N´N с диагональными элементами, равными x0 x1 … xN-1, если xn – это скаляр, или блоковая диагональная матрица размера NM´NM с матрицами размера M´M на главной диагонали, если xn – это матрица размера M´M, где n=0, 1, … N-1. , структура кодового слова
, структура кодового слова  примет вид
примет вид , (1)
, (1) , где
, где  и
и  . Пусть
. Пусть  – информационный вектор, составленный из информационных символов. Если представить информационный вектор
– информационный вектор, составленный из информационных символов. Если представить информационный вектор  в виде
в виде  , то по методике [1] вектор
, то по методике [1] вектор  (i=1, …, J) используется для построения i-го блока кодового слова; а если вектор
(i=1, …, J) используется для построения i-го блока кодового слова; а если вектор  , то вектор
, то вектор  можно использовать для построения j-го слоя блока кодового слова.
можно использовать для построения j-го слоя блока кодового слова. путем умножения справа на матрицу
путем умножения справа на матрицу  , то есть
, то есть . (2)
. (2) . Пусть Y – комплексная матрица вида Y=
. Пусть Y – комплексная матрица вида Y= diag(1 j … jM-1), где
diag(1 j … jM-1), где  . Пусть K – расширение поля
. Пусть K – расширение поля  , где tl – задержка l-го луча (l=1, …, L); Ts – время передачи сигнала. Пусть f – алгебраическое число порядка как минимум NLNqNb над полем K.
, где tl – задержка l-го луча (l=1, …, L); Ts – время передачи сигнала. Пусть f – алгебраическое число порядка как минимум NLNqNb над полем K. , полученных с помощью (2), в вектор
, полученных с помощью (2), в вектор . (3)
. (3) , будем подразумевать любой элемент некоторого слоя. Итак, по методике, вектор
, будем подразумевать любой элемент некоторого слоя. Итак, по методике, вектор  вектор слоев, а
вектор слоев, а  – вектор смещений. Число элементов в векторе
– вектор смещений. Число элементов в векторе  и
и  . Если элемент вектора
. Если элемент вектора  , выполняющую преобразование вектора
, выполняющую преобразование вектора  (4)
(4) . (5)
. (5) и основываясь на выражении (1), можно получить кодовое слово
и основываясь на выражении (1), можно получить кодовое слово  .
. , тогда вектор
, тогда вектор  , где i=1, …, J.
, где i=1, …, J. через xi,j(k)fj-1.
через xi,j(k)fj-1.
 .
. и
и  , получим
, получим .
. и вектор смещений
и вектор смещений , тогда на основе (4) получим матрицу P.
, тогда на основе (4) получим матрицу P.
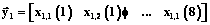
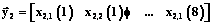 .
. и
и  , из 32 компонент получим кодовый вектор:
, из 32 компонент получим кодовый вектор: .
.
