Факторный анализ в задачах моделирования многомерных систем
| Пащенко Ф.Ф. (feodor@ipu.ru) - Институт проблем управления им. В.А. Трапезникова РАН, г. Москва, доктор технических наук, Дургарян И.С. (durgoft@ipu.ru) - Институт проблем управления им. В.А. Трапезникова РАН, г. Москва, кандидат технических наук, Голяк И.В. (ivgo@bk.ru) - Институт проблем управления им. В.А. Трапезникова РАН, г. Москва | |
| Ключевые слова: корреляция, модель, факторный анализ, факторы, прогноз, идентификация, динамический объект, многомерный объект |
|
| Keywords: correlation, mathematical model, factor analysis, factors, the forecast, identification, a dynamic object, multidimensional object |
|
|
|
|
В процессе создания АСУ нередко некоторые параметры, характеризующие объект и входные процессы, недоступны для наблюдения или не могут быть автоматически измерены из-за отсутствия требуемых датчиков. В таких случаях приходится измерять не искомую величину, а ее косвенные показатели, которые можно контролировать автоматически. Подобные задачи возникают, например, при идентификации иерархических систем, когда взаимосвязи между элементами одного и того же или разных уровней фактически недоступны для наблюдения. Аналогичные ситуации складываются во многих областях промышленности, в экономике, социологии, медицине. Возникает задача построения многоступенчатого алгоритма прогнозирования, что при большой размерности вызывает значительные трудности. Эти трудности и размерность задачи можно существенно уменьшить, используя методы факторного анализа и дисперсионной идентификации. Пусть X(t) – входной сигнал, Y(t) – выходной сигнал идентифицируемого объекта, V(t) – выходной сигнал объекта с известным оператором B, A – оператор идентифицируемого объекта. Предположим, что оператор B имеет ограниченный обратный оператор B–1, тогда ненаблюдаемый входной сигнал можно представить в виде X(t)= =B–1V(t). Уравнение для оценки оператора идентифицируемого объекта при этом можно записать следующим образом: Y(t)=CV(t), где C=A´B–1. Пусть операторы A и B являются линейными нестационарными интегральными операторами. Тогда оценку весовой функции идентифицируемого объекта можно найти из системы интегральных уравнений
Решая данную систему известными методами, получим оценки как для весовой функции, так и для сигнала на входе объекта. При рассмотрении объектов, на входе и выходе которых действуют случайные процессы, решение поставленной задачи можно получить из системы уравнений
где Ky(t, s), Kv(t, s) – известные корреляционные функции сигналов Y(t) и V(t) соответственно; Kx(t, l) – неизвестная корреляционная функция входного сигнала; w(t, t) – известная весовая функция, а g(t, t) – неизвестная. При идентификации нелинейных объектов, а также линейных объектов, на входе которых действуют случайные процессы с нелинейной внутренней структурой, целесообразно применять дисперсионные методы. При этом оценку весовой функции линейного в среднем приближения идентифицируемого объекта можно получить из системы уравнений
В данной системе уравнений предполагается, что входные и выходные процессы являются стационарными и стационарно связанными в дисперсионном смысле [1]. В факторном анализе основным предположением является равенство X=LF+E, (1) где X – вектор-столбец наблюдаемых переменных размерности p´1; L–p´k – матрица факторных нагрузок; F–k´1 – вектор-столбец факторов (k Уравнение (1) постулирует основные предположения факторного анализа о том, что множество наблюдаемых коррелированных переменных X, которые подчиняются многомерному нормальному распределению с корреляционной матрицей C размерности p´p, можно описать меньшим числом гипотетических переменных или факторов F и множеством независимых остатков E. Рассмотрим модель объекта с выходом Y и входом X=(X1, …, Xp). Если p велико, возникает желание сократить размерность модели, выразив ее входы через меньшее количество k
для некоррелированных факторов
для коррелированных факторов
где P – оцененная корреляционная матрица факторов, а матрица L определяется согласно [2]. Модель объекта будем искать по формуле
где B – вектор-столбец неизвестных коэффициентов размерности k´1. Коэффициенты вектора определим из условия минимума функционала
Подставляя (4) в (5) и дифференцируя полученное выражение по В, придем к уравнению
Решая (6) с учетом (2), получим
где Q=LTC–1 – матрица размерности k´p, а матрицы Kxx и Kxy определяются соответственно формулами Для коррелированных факторов получим
Следует отметить, что (7) и (9) получены при условии линейной связи между факторами и входными переменными. Если эта связь нелинейна, то в (7) и (9) вместо (8) будут входить матрицы, элементы которых – дисперсионные функции. Рассмотрим представление ненаблюдаемых входов при помощи модели пространства состояний [3]. Предположим, что некоторый дискретный векторный процесс Y(t) описывается разностным линейным уравнением, которое представимо в форме Yi=AYi–1+ГUi–1, i=0, 1, …, (10) где Yi–n´1 – вектор-столбец состояния системы в момент ti; Ui–1 – векторный гауссовский белый шум; A и Г – постоянные матрицы. Предполагается, что Yi – стационарный гауссовский процесс с заданным начальным состоянием Y0. Пусть процесс Y(t) является входом определенного динамического объекта, для которого требуется построить модель в виде
где Предположим, что в те же дискретные моменты ti вместо вектора Yi измеряется вектор Zi размерности r´1 (r£n), линейно связанный с вектором состояния Yi:
где H – постоянная матрица размерности r´n; Vi – векторный гауссовский белый шум. Вместо вектора Yi в (11) подставим его оценку, оптимальную в смысле некоторого критерия, полученную по наблюдаемому вектору Zi. Наилучшая среднеквадратическая оценка Yi=M{Yi/z1, …, zi} может быть получена при помощи дискретного фильтра Калмана:
где неизвестная матрица Bi определяется из условия минимума среднеквадратической ошибки [1]. Применяя рекуррентную процедуру оценивания, выразим
где I – единичная матрица размерности n´n, а матрицы B1, …, Bi определяются согласно [1]. Без ограничения общности предположим, что математические ожидания векторов Yi и Zi равны нулю для любого момента i; Подставляя в (11) вместо вектора Yi его оценку
где Zi – набор векторов (Zi, Zi–1, …, Z1); элементами матрицы Учитывая (14), формулу (15) можно выразить через корреляционные матрицы процессов Zi и Wi и процессов Zi и Zj, j=1, …, i. Поскольку применение рекуррентной процедуры и определение матриц B1, …, Bi в (14) являются достаточно трудоемкими, используем в (11) другую оценку ненаблюдаемого вектора Yi по наблюдаемым векторам Z1, …, Zi. Проведем следующее преобразование переменных:
Здесь Zi означает набор векторов (Z1, …, Zi). Полученные переменные Xi и Fi связаны соотношением Xi=HFi+Vi, которое по форме аналогично соотношению (11) и в то же время полностью укладывается в рамки модели классического факторного анализа. Используя формулу связи между наблюдаемыми переменными и факторными нагрузками (2), можно получить следующую оценку
Применяя теорию псевдообратных матриц, учитывая (11) и то обстоятельство, что в качестве критерия минимизации применяется квадратичный функционал, (18) можно записать в виде
где H+ – псевдообратная матрица; y – произвольный вектор; I – единичная матрица. В частном случае при y=0 формула (19) принимает вид
Таким образом, модель (15) может быть записана в виде
Матрица коэффициентов P, найденная из условия минимума среднеквадратичного отклонения
Положим, как и выше, математические ожидания Zi и Wi равными нулю. Тогда Из вышесказанного следует, что, используя методы факторного анализа и рекуррентного фильтра Калмана, можно существенно сократить размерность прогнозирующих моделей без ощутимой потери точности. Литература 1. Дисперсионная идентификация; [под ред. Н.С. Райбмана]. М.: Наука, 1981. 2. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. М.: Финансы и статистика, 2000. 3. Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975. 4. Дургарян И.С., Пащенко Ф.Ф. Метод двухступенчатой идентификации в задаче оценки экономической эффективности АСУ // Автоматика и телемеханика. 1977. № 5. 5. Функциональный анализ; [под ред. С.Г. Крейна]. М.: Наука, 1972. |
http://swsys.ru/index.php?id=2714&lang=%E2%8C%A9%3Den&like=1&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Прогнозирование временного ряда инфекционной заболеваемости
- Алгоритм идентификации параметров устройства для нагрева жидкости
- Применение метода многоступенчатой идентификации при разработке математических моделей социально-экономических систем
- Внедрение компьютерных технологий в лабораторный практикум
- Модель сервисного обслуживания компьютерных тренажеров военного назначения
Comments

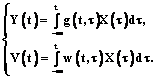
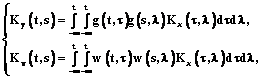
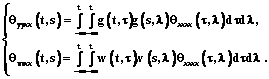
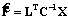 , (2)
, (2)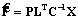 , (3)
, (3)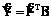 , (4)
, (4)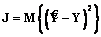 . (5)
. (5)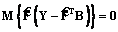 . (6)
. (6)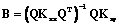 , (7)
, (7)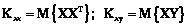 . (8)
. (8)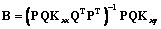 . (9)
. (9)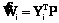 , (11)
, (11)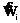 – выход модели в момент ti; P – вектор искомых коэффициентов модели.
– выход модели в момент ti; P – вектор искомых коэффициентов модели.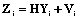 , (12)
, (12)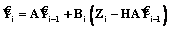 , (13)
, (13)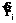 через оценку начального состояния
через оценку начального состояния 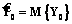 и значения наблюдаемых векторов Z1, …, Zi:
и значения наблюдаемых векторов Z1, …, Zi: (14)
(14)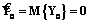 . Тогда справедливы равенства
. Тогда справедливы равенства 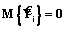 и
и 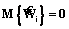 для любого i.
для любого i. и применяя аналогично предыдущему случаю среднеквадратический критерий для оценки вектора коэффициентов P, получим
и применяя аналогично предыдущему случаю среднеквадратический критерий для оценки вектора коэффициентов P, получим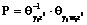 , (15)
, (15)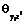 являются множественные дисперсионные функции, а элементами матрицы
являются множественные дисперсионные функции, а элементами матрицы 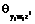 – множественные обобщенные дисперсионные функции.
– множественные обобщенные дисперсионные функции.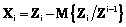 , (16)
, (16)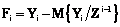 . (17)
. (17)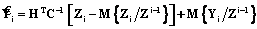 . (18)
. (18)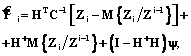 (19)
(19)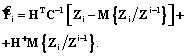 (20)
(20) (21)
(21) от W, имеет вид
от W, имеет вид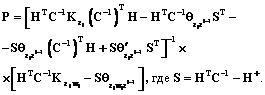 (22)
(22)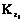 будет являться автокорреляционной матрицей векторного процесса Zi;
будет являться автокорреляционной матрицей векторного процесса Zi;  – взаимной корреляционной матрицей векторных процессов Zi и Wi;
– взаимной корреляционной матрицей векторных процессов Zi и Wi; 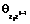 состоит из множества дисперсионных функций векторного процесса Zi относительно Zi–1;
состоит из множества дисперсионных функций векторного процесса Zi относительно Zi–1; 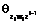 – из множественных обобщенных дисперсионных функций векторных процессов Zi и Wi относительно Zi–1;
– из множественных обобщенных дисперсионных функций векторных процессов Zi и Wi относительно Zi–1; 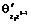 – из множественных дисперсионных функций векторных процессов Zi и Zi–1.
– из множественных дисперсионных функций векторных процессов Zi и Zi–1.