Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Формальная модель предметной области на основе нечетких отношений
Аннотация:В условиях применения автоматизированных систем происходит трансформация функций человека. При этом, несмотря на то, что затраты на получение и переработку информации непрерывно возрастают, остаются неисследо-ванными многие теоретические аспекты, связанные с моделированием процессов автоматизации и информационным сопровождением совместно с семантическими правилами, их регламентирующими. В статье предложен вариант мо-делирования предметной области с позиций методов, учитывающих нечеткость описаний модели исследуемого объ-екта.
Abstract:In conditions of application of the automated systems there is a transformation of functions of the person. Thus in spite of the fact that the share of expenses for reception and processing of the information continuously grows, there are unexplored many theoretical aspects connected to modelling of processes of automation and information support together with semantic rules their regulating. In article the variant of modelling of a subject domain from positions of the methods which are taking into account an illegibility of descriptions of model of researched object is offered.
| Авторы: Антонов В.В. (antonov.v@bashkortostan.ru) - Уфимский государственный авиационный технический университет, факультет ИРТ (профессор), Уфа, Россия, доктор технических наук, Куликов Г.Г. (gennadyg_98@Yahoo.com) - Уфимский государственный авиационный технический университет, г. Уфа, Россия, кандидат технических наук | |
| Ключевые слова: формальный алгоритм, метод семантических дифференциалов, параметрическая адекватность, методология структурного анализа, семантическая модель, предметная область |
|
| Keywords: formal algorithm, method of semantic differentials, parametrical adequacy, methodology of the structural analysis, semantic model, subject domain |
|
| Количество просмотров: 15693 |
Версия для печати Выпуск в формате PDF (5.35Мб) Скачать обложку в формате PDF (1.27Мб) |
Перевод условий практической задачи на язык математических моделей всегда был сложным и зачастую приводил к потере трудноформализуемой качественной информации. Многие современные задачи управления просто невозможно решить классическими методами из-за очень большой сложности математических моделей, их описывающих. Процесс начинается с выделения объектов предметной области и выявления связей между ними. Функцию выбора можно представить в виде множества альтернативных объектов, выбираемых по некому условию, которое, в свою очередь, может быть представлено как совокупность сведений о состоянии объекта и множестве правил выбора. Пусть s – совокупность сведений, характери- зующих объекты; Z – множество объектов предметной области; ziÎZ – объект из множества объектов. Очевидно, что часть сведений, характеризующих объект, можно представить в виде множества его информационных характеристик: xi={áAi, Diñ½xiÌs}, где Ai – непустое множество имен свойств (атрибутов) i-го объекта; Di – множество значений соответствующих атрибутов; xi – множество информационных характеристик i-го объекта. Может быть составлен словарь элементов допустимых значений, подразделенный на классы, что позволяет представить предметную область в виде иерархической структуры. Значения разбиваются на классы объектов, которые взаимодействуют друг с другом на основе правил. Пусть p – множество правил выбора, тогда условия выбора объекта из множества альтернатив можно представить в виде кортежа y=ás, pñ. На множестве атрибутов могут быть установлены отношения Таким образом, информацию об объекте ziÎZ можно представить как совокупность информационных характеристик объекта, установленных отношений и правил установления отношений zi={xi, G, p} Тогда в качестве нечеткой характеристики объекта xi можно взять нечеткое множество Таким образом, предметную область можно представить в виде многоуровневой среды, состоящей из множества элементов предметной области, множества функций и методов, работающих на этих элементах, и множества свойств элементов и отношений между элементами, то есть в виде онтологии, которая включает в себя описание свойств предметной области и взаимодействия объектов на некотором формальном языке, имеющем логическую семантику. Если система сложная, число факторов велико, то учесть все ее характеристики (компоненты) чрезвычайно сложно. Поэтому в модель приходится вводить лишь ограниченное число компонентов, а оставшиеся учитывать явно, не вводя в модель, но беря во внимание их влияние как нечеткую реакцию модели на выбор той или иной альтернативы. Очевидно, что алгебраическое сравнение компонентов невозможно и может быть выполнено с применением методов нечеткой логики. При этом конечное множество объектов предметной области может использоваться в качестве множества объектов кластеризации. Данное множество описывается конечным множеством атрибутов, каждый из которых количественно представляет некоторое свойство или характеристику элементов рассматриваемой предметной области. Использование средств нечеткой логики позволяет утверждать, что для каждого объекта в некоторой количественной шкале измерены все значения атрибутов, то есть каждому объекту поставлен в соответствие вектор, координатами которого являются количественные значения соответствующих атрибутов. После задания степеней принадлежности можно вычислить координаты центров кластеров. Выбор наиболее предпочтительного решения в каждом конкретном случае может осуществляться по совокупности сложных критериев с нормировкой его компонентов. Учитывая, что в данном случае представляет интерес только множество четко недоминируемых решений, исключая отношение равноценности, используя доказательства, приведенные в работе [1], с помощью выбора альтернатив на основе b-уровневых отношений предпочтения решение сводится к многокритериальной задаче, где в качестве критериев эффективности выступают функции принадлежности, и в конечном итоге – к вычислению одной функции по формальному алгоритму решения b-уровневых моделей задач принятия решений. Модель, охватывающая информационную систему, можно представить в виде метабазы, в которой содержится информация по каждому виду объекта учета. С другой стороны, информационная система представима в виде функциональной системы, то есть в виде множества функций. Таким образом, цели и ограничения могут быть заданы как нечеткие множества. Взаимосвязь между ними можно определить отношением на декартовом произведении [2]. Рассматривая цели и ограничения в виде симметричных элементов логической схемы, можно достаточно просто сформировать на их основе решение, которое по существу является выбором одной или нескольких из имеющихся альтернатив. При исследовании предметной области может быть получено значительное количество информации субъективного характера. Ее представление на естественном языке содержит нечеткости или неопределенности, не имеющие аналогов на языке традиционной математики. Согласно данным исследовательской организации Gartner Group, почти половина проектов по реализации информационной системы не являются успешными. Основная проблема в неформализованности процесса моделирования предметной области, что делает невозможным применение математических методов анализа свойств моделей предметной области, таких как функциональная полнота и целостность. Все это ставит вопрос о рассмотрении задачи моделирования предметной области с позиций методов, учитывающих нечеткость или неопределенность описаний модели исследуемого объекта. Любое явление представляет собой известное единство качества и количества. Это единство фиксируется в философии понятием меры объекта. Пространство и время сами по себе не есть материя, это лишь способы ее бытия, выражающие тот эмпирический факт, что все вещи, события и процессы находятся в ситуации соподчинения и координации [3]. Существование во времени означает порядок их следования друг за другом, цикличность и определенную ритмику изменения, а отличительными признаками пространства и времени как атрибутов материи являются их протяженность и длительность. Говорить о предметной области есть смысл, если она имеет определенную семантическую локализацию, например, в пространстве и времени, или функциональную. Тогда построение семантической модели сводится к формализации логических отношений. Математический подход позволяет ограничиться множеством цепочек, которые можно определить точно. То есть можно говорить о неком формальном языке, заданном в виде множества. Для построения необходимо иметь алгоритм, который по заданной грамматике строит вывод, порождаемый этой грамматикой. Отсюда следует, что любая функция, определенная на дереве вывода, может быть представлена в виде атрибута какого-либо определенного узла. Предметную область можно декомпозировать на элементарные объекты, каждый из которых описывается совокупностью атрибутов. Объекты предметной области связаны между собой определенными отношениями, которые в совокупности представимы в виде взвешенного по ребрам частично ориентированного графа. Структура графа представляет структуру предметной области, а подграфы графа – сложные объекты, или подсистемы предметной области. Вместо графов для представления структуры предметной области можно использовать язык теории множеств и решеток их разбиений. Каждый кортеж БД – это описание состояния некоторого элементарного объекта. Подмножество всех кортежей, сходных с данным кортежем относительно выбранной меры сходства, является представлением элементарного объекта. Пусть W – исследуемая предметная область объектов W={w1, …, wn}, при этом нечеткость знаний или отношений может определяться семантикой самой информации. Не включенные в выделенные предметные области свойства можно рассмотреть как отдельную предметную область с особыми свойствами – окружающую среду. Таким образом, любая предметная область может считаться распределенной, так как она взаимодействует с окружающей средой. В соответствии со сказанным Пусть S – модель предметной области объектов FM:W®S. Каждому объекту предметной области может быть поставлена в соответствие модель (на основании функции моделирования FM) Сопоставляя полученные результаты, можно сделать вывод, что они будут одинаковыми независимо от того, выполнена ли сначала операция в предметной области, а затем произведено отображение на модель предметной области, или наоборот. Таким образом, этап построения семантической модели предметной области можно определить как формализацию зафиксированных в описании логических отношений. Модель предметной области S может быть представлена в виде метабазы, в которой содержится информация по каждому элементу структуры. С другой стороны, предметную область W можно также представить в виде множества. Введем обозначение P – множество свойств, определяемых связями элементов указанных выше множеств. Тогда взаимосвязь между ними может быть определена отношением на декартовом произведении P´S´W={(pi, ri, wi): piÎP, riÎS, wiÎW, i=1, …, n}. Принадлежность элемента zi=(pi, ri, wi), где piÎP, riÎS, wiÎW, i=1, …, n, данному отношению интерпретируется следующим образом: в объекте модели предметной области ri содержится информация по свойству pi объекта предметной области wi. Поиск информации, соответствующей конкретному элементу модели предметной области ri в объекте предметной области wi, сводится к определению отношения RÍS´W. Таким образом, о любой паре (ri, wi)ÎR: riÎS, wiÎW, i=1, …, n, можно сказать, что wi является релевантным ri, и решение задачи определения релевантности элементов множеств S и W сводится к определению отношения RÍS´W. В качестве схем информационных объектов рассматриваемой модели могут быть определены независимые бизнес-процессы [4]. Учитывая построение модели в виде объектов, каждый независимый бизнес-процесс можно рассматривать как отдельную (обособленную) часть информационной системы. Учитывая, что данная система разделена на информационные объекты, объединенные по семантическим правилам взаимодействия, можно декларировать относительную полноту множества учитываемых отношений между элементами системы, которые определяют ее пове- дение и являются предметом анализа функциональной надежности. Таким образом, отношения между взаимодействующими бизнес-процессами можно классифицировать на основе математических правил четкой и нечеткой логик. Концепция построения такой системы фактически отражает современную стратегию так называемых CALS-технологий и может рассматриваться как инструмент повышения эффективности и качества, так как полностью соответствует духу и принципам международных стандартов серии ISO-9000. Литература 1. Погонин В.А. Модели диспетчерского управления роботами // Информационные процессы и управление (Интернет-журнал). 2006. № 1. С. 45–57. 2. Бениаминов Е.М. Алгебраические методы в теории баз данных и представлении знаний. М.: Научный мир, 2003. 184 с. 3. Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решений на основе нечетких моделей. Примеры использования. Рига: Зинатне, 1990. 180 с. 4. Куликов Г.Г., Антонов В.В. Метод формирования структуры хранилища данных для автоматизированной учетной системы на основе процессного анализа предметной области: сб. науч. тр. // Вестн. УГАТУ. Уфа: УГАТУ. 2006. Т. 8. № 1(17). С. 60–67. 5. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях: сб. науч. тр. М.: Мир, 1976. С. 172–215. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=2761&like=1&page=article |
Версия для печати Выпуск в формате PDF (5.35Мб) Скачать обложку в формате PDF (1.27Мб) |
| Статья опубликована в выпуске журнала № 2 за 2011 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Семантико-математический язык описания структуры интеллектуальной системы на основе нечеткой логики
- Определение границ предметной области при прогнозировании развития предприятия
- Метод автоматизированного формирования семантической модели базы данных диалоговой системы
- Информационная подсистема оценки рейтинга профессорско-преподавательского состава
- Логический анализ корректирующих операций для построения качественного алгоритма распознавания
Назад, к списку статей



 , которые делятся на количественные
, которые делятся на количественные  и качественные
и качественные  , а также определено множество типов выбора, например, T={соответствие, эквивалентность, предпочтение}. Тогда любое правило выбора может быть представлено кортежем p=áG, Tñ.
, а также определено множество типов выбора, например, T={соответствие, эквивалентность, предпочтение}. Тогда любое правило выбора может быть представлено кортежем p=áG, Tñ. , iÎN. Значения атрибутов могут носить нечисловой характер. В частности, в макроэкономических, социологических, маркетинговых, медицинских, правовых хранилищах данных широко используется лингвистическая форма представления данных. В общем случае характеристика каждого объекта xi может быть описана соответствующей лингвистической переменной áAj, Tj, Djñ, где
, iÎN. Значения атрибутов могут носить нечисловой характер. В частности, в макроэкономических, социологических, маркетинговых, медицинских, правовых хранилищах данных широко используется лингвистическая форма представления данных. В общем случае характеристика каждого объекта xi может быть описана соответствующей лингвистической переменной áAj, Tj, Djñ, где  – терм-множество лингвистической переменной Aj (набор лингвистических значений атрибута); mj – число значений атрибута; Dj – (предметная шкала) базовое множество атрибута Aj. Для описания термов
– терм-множество лингвистической переменной Aj (набор лингвистических значений атрибута); mj – число значений атрибута; Dj – (предметная шкала) базовое множество атрибута Aj. Для описания термов  , k=1, …, mj, соответствующих значениям атрибута Aj, могут использоваться нечеткие переменные
, k=1, …, mj, соответствующих значениям атрибута Aj, могут использоваться нечеткие переменные  то есть значение
то есть значение 

 dÎDj, k=1, …, mj, в базовом множестве Dj.
dÎDj, k=1, …, mj, в базовом множестве Dj. ,
,  ,
,  .
. , где
, где  не является функцией в обычном понимании, а лишь определяет возможное состояние предметной области одного объекта на основе отличия от другого.
не является функцией в обычном понимании, а лишь определяет возможное состояние предметной области одного объекта на основе отличия от другого. . Таким образом, каждому объекту wiÎW соответствует riÎS. При этом должна присутствовать функция
. Таким образом, каждому объекту wiÎW соответствует riÎS. При этом должна присутствовать функция  , которая однозначно определяет ri+1 по ri, то есть
, которая однозначно определяет ri+1 по ri, то есть  . Очевидно, что ri+1 может быть определено по цепочке
. Очевидно, что ri+1 может быть определено по цепочке  . После подстановки получаем
. После подстановки получаем  . С другой стороны, существует по меньшей мере еще одна цепочка
. С другой стороны, существует по меньшей мере еще одна цепочка 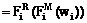 .
.