Программные продукты и системы

Существует много методик расчетов оптимальных настроек регуляторов систем автоматического регулирования (САР), разработанных на основе теоретических аналитических исследований систем регулирования и базирующихся на определенных представлениях их авторов о критериях оптимальности: степени затухания, интегральной ошибке и т.п. Так, в [1] предлагаются формулы для расчета оптимального ПИ-регулято­ра объекта с запаздыванием, с минимальным временем переходного процесса, с заданным перерегулированием, с минимальным интегральным отклонением; в [2] – с заданным показателем колебательности (обычно равным 1,62) и т.д.

Большинство авторов не различают настройки, оптимальные для переходных процессов по управлению и по возмущению, хотя для разных технологических процессов более важными являются то те, то другие в зависимости от того, требуется ли стабилизация параметров или осуществляется программное управление. Настройки, в некотором смысле оптимальные для системы стабилизации, могут оказаться совершенно непригодными для процесса, в котором по технологическим причинам несколько раз значительно меняется задание регулятору.

Современные математические пакеты вполне позволяют подбирать настройки исходя из естественного интегрального критерия оптимизации

,      (1)

где KИ, KП – настройки регулятора; y*(t) – задание; y(t, KИ, KП) – выходная величина объекта, получаемая путем имитационного эксперимента на модели; tmax – время переходного процесса [3].

Реализовав модель САР в среде Simulink пакета Matlab 6.5, осуществляем передачу ей параметров из пакета MS Excel через VBA-программу с использованием оператора MLPutVar расширения Excllink, входящего в комплект поставки Matlab. Использование MS Excel не только привычно и удобно для представления результатов расчетов, но и позволяет наглядно отображать процесс подбора параметров и исследовать чувствительность САР к их изменению. Минимизация критерия производится любым численным методом, например, покоординатного спуска или градиентным, который можно реализовать как в Matlab, так и в VBA-программе. Так, для ПИ-регулятора объекта с передаточной функцией  была получена поверхность зависимости критерия (1) от настроек регулятора, представленная на рисунке 1. Очевидно, что чувствительность САР к изменению KП меньше, чем к изменению KИ. Подобные поверхности можно строить также для исследования чувствительности САР к изменению параметров самого объекта, что актуально для исследования промышленных систем с нестационарными параметрами.

Дальнейшие исследования показывают, что вследствие погрешностей расчетов в окрестности минимума наблюдается довольно значительный шум критерия (1) (см. рис. 2).

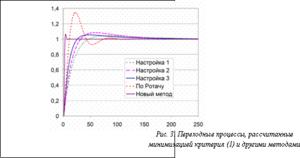
Нивелировать погрешность можно, сгладив получающуюся поверхность F(KИ, KП) полиномом второго или третьего порядков. Для широкого круга объектов описанный метод дает возможность получить значительно более качественные переходные процессы, чем методы из работ [1] и [2]. На рисунке 3 приведены примеры переходных процессов по управлению для объекта с передаточной функцией , полученные при трех вариантах настройки: по А.П. Копеловичу, по В.Я. Ротачу и настройке предлагаемым методом. Отметим, что для объектов с меньшим запаздыванием качество процессов при переходе на новый метод расчета возрастает.

При использовании критерия (1), а также квадратичного интегрального критерия

  (2)

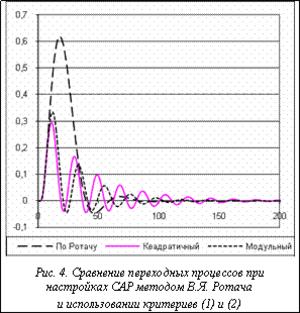
для некоторых объектов возрастает колебательность процесса (рис. 4).

Поэтому предлагается использовать критерий

  (3)

где N1,2 – количество выходов переходного процесса вверх и вниз за пределы заданной погрешности регулирования (обычно ±5 % в относительных величинах), tmin объяснено ниже. Сумма N1+N2 увеличена на 1, чтобы значение критерия в случае, если переходный процесс не выходит за пределы коридора вокруг заданного значения, не было тождественно равно нулю. Задача оптимизации остается прежней.

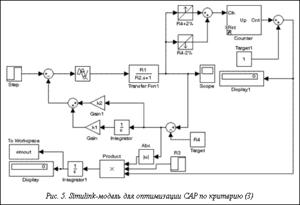
Модель Simulink, позволяющая рассчитывать значение критерия (3), приведена на рисунке 5.

Ее использование позволяет исследовать переходные процессы по управлению и возмущению, а также при заданном соотношении управления и возмущения в ходе технологического процесса. В блоке Step, моделирующем единичное воздействие по возмущению, устанавливается задержка, превышающая продолжительность переходного процесса по управлению. Задержка блока R3, моделирующего единичный ступенчатый сигнал, позволяет интегрировать ошибку только после заданного момента tmin. Например, нет смысла интегрировать ошибку (3) до момента t

Зависимость оптимальных настроек ПИ-регулятора от значения R4

Полученные оптимальные настройки регулятора для объекта с передаточной функцией  приведены в таблице и на рисунке 6. Интересно, что зависимость KИ(R4) хорошо подчиняется линейному закону KИ(R4)=0,092–0,011´R4 с коэффициентом корреляции 0,9902.

Таким образом, разработанный метод поиска оптимальных настроек регуляторов по критериям модульной интегральной ошибки или модульной интегральной ошибки с учетом колебательности переходного процесса может использоваться для определения настроек позиционного или непрерывного регулятора объекта с запаздыванием. Метод позволяет корректировать оптимальные настройки регулятора в зависимости от того, какая задача является более важной: обеспечить качество переходных процессов по возмущению, по управлению или при заданном соотношении «управление–возмущение». Полученные настройки в общем случае обеспечивают несколько более качественные переходные процессы по управлению и (или) по возмущению, чем при использовании настроек, рассчитанных методами В.Я. Ротача и А.П. Копеловича.

Литература

1. Копелович А.П. Инженерные методы расчета при выборе автоматических регуляторов. М.: Металлургиздат, 1960. 190 с.

2. Ротач В.Я. Теория автоматического управления. М.: Изд-во МЭИ, 2004. 400 с.

3. Затонский А.В. Компенсация недоступности информации в подсистеме управления сложной технической системой // Математические методы в технике и технологиях: сб. науч. тр. Междунар. науч. конф. Саратов, 2008. Вып. 21. Т. 2. С. 54–58.